AHP-层次分析法(C++源码，附详细注释和样例）

原文链接http://ipipblog.net/article/show?aid=16 转载请注明

算法简介

AHP-层次分析法是数学建模中的常用算法，其适用于一批非常广泛的问题，综合来说，它是一个“层次权重决策分析方法”。客观地讲，它适用于一些有限制条件的决策选择问题:

1.    决策有限，且只从有限的候选决策里选择。
2.    决策的影响因素已知，因素的关系（包括隶属关系和优先级关系）已知
3.    因素的关系不论客观与否，要通过合理性校验，即必须是合理的关系才能导出合理的决策。

算法流程

以下例子以旅游选地点为例。

数据统计阶段

步骤1.获取目标层和决策层，对于旅游问题来说，需要得到候选旅游地点作为决策层，目标层为最后得出的决策。

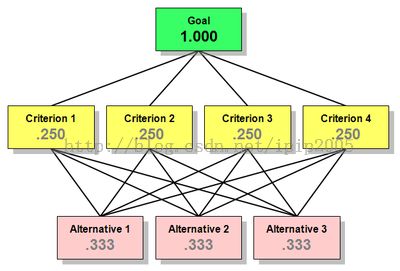
步骤2.获取中间层信息。除决策层外的每一节点（包括中间层的所有节点和目标层节点），与影响它的节点相连，构造阶梯层次结构，保证为一个有且仅有层与层之间连边的分层图。大概样子如下(from维基）：

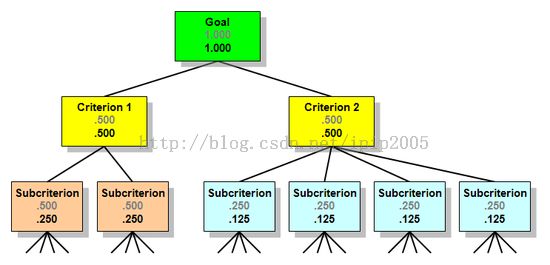
    当然，中间层可以不止一层，层与层之间也不一定是全连边的，比如：

步骤3.构造成对比较矩阵，对每一个除最底层（决策层，所有的Alternative）的节点，构造该点的成对比较矩阵。该点的成对比较矩阵的含义是所有影响它的因素两两之间的优先级关系。比如上图中Criterion的成对比较矩阵应是一个表示两个Subcriterion优先级关系的2x2矩阵；Criterion2的成对比较矩阵则是4个蓝色的Subcriterion优先级关系的4x4矩阵。

    而优先级关系，一般情况下只用1~9的整数数值来表示。我想一个原因是这个关系通常是主观得到的，过于精细或者过于大的数值都失去了意义；另一个原因在后面会提到，一般情况下设置为1~9已经足够通过合理性（或者叫做一致性检验）了。

一致性检验

    一致性检验是整个决策算法可以实施的最为重要的一步，无论你前面的元素关系和成对比较矩阵怎么设置，如果检验结果很差，那么说明优先级关系不太合理（比如A：B=3，B:C=3，A:C=1/9这种不合理的情况）。检验的结果主要依赖于单个矩阵的一致性检验，和综合情况的一致性检验。

    检验的目的主要是判定整个决策过程是否是基于某个近似“所有元素都有一个假想权值”的情况。该问题的本质，也就是求出这组假象的权值，使得我们可以根据这组权值轻松地作出决策。所以一致性检验做的，并不是检查是否有错误的优先级关系，而是检查是否所有的优先级关系满足或近似满足上述“所有元素都有一个假想权值”的情况，越靠近这种情况，检验结果越好。

一致性检验:单个矩阵的一致性检验

    单个矩阵的检验的目的，就是为了定量得出该矩阵与“一致阵”的“差距”。

    所谓一致阵A，定义上讲，就是对任意i,j,k，成立Aik*Akj=Aij。通俗地讲，就是存在一组权值，A的每一个位Aij都代表了权值i和权值j的比值。显然，一致阵是最合理的成对比较矩阵。一致阵的例子：

ω:

   

ω1

ω2

ω3

ω4

ω5

A:

1	ω1/ω2	ω1/ω3	ω1/ω4	ω1/ω5
ω2/ω1	1	ω2/ω3	ω2/ω4	ω2/ω5
ω3/ω1	ω3/ω2	1	ω3/ω4	ω3/ω5
ω4/ω1	ω4/ω2	ω4/ω3	1	ω4/ω5
ω5/ω1	ω5/ω2	ω5/ω3	ω5/ω4	1

    

    我们自己设定的矩阵一般都不是一致阵，怎样衡量它和一致阵的“差距”？

    先考虑这种情况，如果我们已知一致阵，但不知道权值向量，我们怎么通过矩阵求权向量？答案很简单，就是求该一致阵的最大特征根（等于n），然后求出该特征根对应的特征向量作为权值向量（各个行/列向量都对应特征根n），其实任意一行/列都能看出权向量的关系不是么？

    考虑矩阵不是一致阵的情况，因此我们可以类似地先求出矩阵的最大特征根λ，再求出λ对应的归一化权向量ω（以后统称权向量）就可以了,则有Aω=λω，这个称为特征根法。归一化的目的是为了计算每个点的实际选择权值（每层实际和值为1），或称到达“概率”。

    可知λ≥n，在A不是一致阵的情况下，有λ>n,因此我们可以用λ-n的数值来衡量A的与一致阵的“差距”。由此可以定义一致性指标：

    

    

    接下来的问题是——如何判断这个CI是合格的？

    定义 随机一致性指标RI，代表了在矩阵随机的情况下，矩阵的一致性指标的CI的均值。当然我们不能枚举所有可能的矩阵，所以用随机构造大量成对比较矩阵的方法来近似得到这个均值。

    定义 一致性合格比Δ，只要我们构造的那个成对比较矩阵的CI<RI*Δ,就可以认为我们的矩阵是通过一致性检验的，即它是合理的。一般取Δ=0.1。不太恰当但通俗地说，如果你构造的矩阵A，它与一致性矩阵的“差距”比随机情况下的“差距”乘上Δ还要小，我们认为A是合格的成对比较矩阵。

一致性检验：综合情况的一致性检验

    我们已经可以判断每一个成对比较矩阵是否是“合理”的了，那么怎么判断它们综合起来是否合理呢？

    现在所有成对比较矩阵均是合理的，那么对于目标层和第一中间层来说，已经可以求出第一层的到达“概率”，也就是我们求得的目标层权向量，它代表了第一层中间层的每一个元素对于目标层的“重要性”，那么对于第二中间层来说，每个元素的“重要性”是通过目标层的权向量和第一层每个元素的权向量加权相乘得到的。我们要求的就是决策层的到达“概率”

    另外一个考量就是，因为可以通过每层的权向量和层与层之间的连边关系求出最后一层的到达“概率”了，所以最后一层（决策层）的到达“概率”就足以决定目标层的决策了。这也符合我们的预期：从决策层找到权值最大的一个最为目标层的决策。所以检验步骤最后的最后，就是检验决策层的权向量是否“合理”。

    利用已经计算出的一些CI、RI值，定义

    其中这m个CI和RI值分别是最后一层中间层（决策层的上一层）的成对比较矩阵的CI和RI值。只要CR <Δ，就认为通过了综合情况的一致性检验。

一致性检验：如果通不过一致性检验

    如果构造的成对比较矩阵通过了一致性检验，那么可以直接用决策层的到达“概率”，取出值最大的决策就可以了。如果通不过一致性检验，则应该考虑重新统计每个成对比较矩阵了。不合理的优先级关系导出的最优决策是不适合作为最优决策的。

得出决策

    由于是树形层次结构，我们只要从目标层广度遍历所有点，求出决策层的到达“概率”就可以了。理论上我们应该选择到达“概率”最大的决策作为目标决策。

C++源码

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
struct node{
    int child[256]; //每个节点的儿子数字，child[0]为儿子个数 
    char name[256]; //节点的名称 
    double** comp;  //该节点概率下的下一层成对比较矩阵 
    double CI;      //CI值 
    double* w;      //最大特征值对应的特征向量 
    double p;       //到达该节点的概率 
    double value;   //只对方案层有效，选取该方案的权重 
}* Node;
struct level{
    int num, start_id;//每一层的点数，和起始点的编号 
}* L;
int n_level, n_node; //总层数，总点数 
/*
 * 初始化经验RI数组 
 */
double RI[12]={0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.51};
/*
 * 寻找字符c在字符串s中的位置，不存在返回-1
 */ 
int pos(char c, char* s){
    int len = strlen(s);
    for (int i = 0; i < len; i++){
        if (s[i] == c) return i;
    }  
    return -1;
}
/*
 * 读入一个double或者分数形式的数字 
 */
void myScanf(double* p){
    char value[256];
    scanf("%s",value);
    int place;
    if ((place = pos('/', value))>0){
       int f = 0, b = 0;
       for (int i = 0; i < place; i++){
           f = f * 10 + value[i] - '0';
       }
       for (int i = place + 1; i < strlen(value); i++){
           b = b * 10 + value[i] - '0';
       }
       *p = 1.0 * f / b;
    } else{
       *p = 0;
       for (int i = 0; i < strlen(value); i++){
           *p = *p * 10 + value[i] - '0';
       }
    }
}
/*
 * 数据输入过程 
 */
void input()
{
    printf("输入总层数，包括目标层和方案层:\n");
    scanf("%d", &n_level);
    printf("已输入\n");
     
    L = new level[n_level];
    n_node = 0;
    printf("从上往下，输入每层个数:\n");
    for (int i = 0; i < n_level; i++){
        scanf("%d",&L[i].num);
        L[i].start_id = n_node;
        n_node += L[i].num;       
    } 
    printf("已输入\n");
 
    Node = new node[n_node];
    printf("从上往下，输入每层属性名:\n");
    for (int i = 0; i < n_node; i++){
        Node[i].child[0] = 0;
        Node[i].p = 0;
        Node[i].value = 0;
        scanf("%s",Node[i].name);
    }
    printf("已输入\n");
    printf("从上往下，输入层与层之间的关系矩阵:\n");
    for (int i = 0; i < n_level - 1; i++){
        for (int j = 0; j < L[i].num; j++)
        for (int k = 0; k < L[i+1].num; k++){
            int ifConnect;
            scanf("%d",&ifConnect);
            if (ifConnect){
               int cur = L[i].start_id + j;
               Node[cur].child[0]++;
               Node[cur].child[Node[cur].child[0]] = L[i+1].start_id + k;
            }
        }
    }
    printf("已输入\n");
     
    printf("从上往下，输入成对比较矩阵:\n");
    for (int i = 0; i < n_level - 1; i++){
        for (int j = 0; j < L[i].num; j++){
            int cur = L[i].start_id + j;
            int size = Node[cur].child[0];
            Node[cur].comp = new double*[size];
            for (int k = 0; k < size; k++) Node[cur].comp[k] = new double[size];
            for (int li = 0; li < size; li++)
                for (int lj = 0; lj < size; lj++)
                    myScanf(&Node[cur].comp[li][lj]);
        }
    }
    printf("已输入\n");
}
/*
 * 程序中止，并输出原因 
 */
void alert(char* p){
    printf("%s回车退出\n", p);
    freopen("CON", "r", stdin);
    system("pause");
    exit(0);
}
/*
 * n阶矩阵matrix和w相乘，并归一化w
 * retDiv为归一化的倍数，返回归一化后的矩阵 
 */
double* normalize(double** matrix, double* w, int n, double* retDiv){
    double* ret = new double[n];
    for (int i = 0; i < n; i++) ret[i] = 0;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++) {
            ret[i] += matrix[i][j] * w[j];
        }
    double sum = 0;
    for (int i = 0; i < n; i++) sum += ret[i];
    for (int i = 0; i < n; i++) ret[i]/=sum;
    *retDiv = sum;
    return ret;
}
/*
 * 检查节点编号为id的节点的成对比较矩阵是否通过一致性检验 
 */
bool checkCR(int id){
    double** matrix = Node[id].comp;
    int n = Node[id].child[0];
    double *w = new double[n], *w_new = new double[n];
    for (int i = 0; i < n; i++) w_new[i] = 1;
    double eps = 1e-10;
    double* retDiv = new double;
    w_new = normalize(matrix, w_new, n, retDiv);
    while (true){
          w = w_new;
          w_new = normalize(matrix, w, n, retDiv);
          bool flag = true;
          for (int i = 0; i < n; i++) 
              if (w[i] - w_new[i] > eps || w[i] - w_new[i] < -eps){
                       flag=false;
                       break;
              }
          if (flag) break;
    }
    Node[id].w = w_new;
    double ans= 0;
    for (int i = 0; i < n; i++)
        ans += w_new[i]/w[i];
    ans = ans * (*retDiv) / n; 
    double CI = (ans - n)/(n-1);
    Node[id].CI = CI;
    if (CI < 0.1 * RI[n]) return true;
    return false;
}
/*
 * 所有单排序权向量的一致性检验 
 */
void checkSingleMatrix(){
    for (int i = 0; i < n_level - 1; i++){
        for (int j = 0; j < L[i].num; j++){
            int cur = L[i].start_id + j;
            if (!checkCR(cur)) {
               printf("第%d层%d号元素<name: %s>的成对比较矩阵无法通过校验,请重新设计",
                   i, j, Node[cur].name);
               alert("");
            }
             
        }
    }
}
/*
 * 总排序权向量的一致性检验 
 */
void checkTotal(){
    double CR = 0;
    Node[0].p = 1;
    /*
     * 计算最后一层中间层的到达概率，即“重要性”
    */
    for (int i = 0; i < n_level - 2; i++){
        for (int j = 0; j < L[i].num; j++){
            int cur = L[i].start_id + j;
            for (int k = 1; k <= Node[cur].child[0]; k++){
                int child = Node[cur].child[k];
                Node[child].p += Node[cur].p * Node[cur].w[k-1];
            }
        }
    }
    int cL = n_level - 2;
    double sumaCI = 0, sumaRI = 0;
    for (int j = 0; j < L[cL].num; j++){
        int cur = L[cL].start_id + j;
        sumaCI += Node[cur].p * Node[cur].CI;
        sumaRI += Node[cur].p * RI[Node[cur].child[0]];
    }
    CR = sumaCI / sumaRI;
    printf("CR值: %.5lf\n",CR);
    if (CR >= 0.1){
        alert("无法通过总排序权向量的一致性检验，请重新设计\n"); 
    }
    printf("检验通过\n"); 
};
/*
 * 根据经检验后的权重，设计最终方案，比较并选择最优解。 
 */
void design(){
    int cL = n_level - 2;
    for (int j = 0; j < L[cL].num; j++){
        int cur = L[cL].start_id + j;
        for (int k = 1; k<= Node[cur].child[0]; k++){
            int child = Node[cur].child[k];
            Node[child].value += Node[cur].p * Node[cur].w[k-1];
        }
    }
    cL = n_level - 1;
    double maxValue = -1e10;
    int maxPlace = -1;
    for (int j = 0; j < L[cL].num; j++){
        int cur = L[cL].start_id + j;
        if (Node[cur].value > maxValue){
           maxValue = Node[cur].value;
           maxPlace = cur;
        }
        printf("<%s>: %.5lf  ", Node[cur].name, Node[cur].value);
    }
    printf("\n\n");
    printf("最优方案为<%s>, 权重为<%.5lf>\n", Node[maxPlace].name, Node[maxPlace].value);
};
/*
 * 整个计算过程 
 */
void calc(){
    printf("单排序权向量一致性检验\n"); 
    checkSingleMatrix();
    printf("检验通过\n"); 
    printf("总排序权向量一致性检验\n"); 
    checkTotal();
    printf("计算方案权值\n");
    design();
    freopen("CON", "r", stdin);
    system("pause");
}
int main()
{
    freopen("level_input.txt","r",stdin);
    input();
    calc();
}

输入数据文件level_input.txt

3
 
1 5 3
 
决策
景色 费用 居住 饮食 旅途
苏州 杭州 桂林
 
1 1 1 1 1
 
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
 
1 1/2 4 3 3
2 1 7 5 5
1/4 1/7 1 1/2 1/3
1/3 1/5 2 1 1
1/3 1/5 3 1 1
 
1 2 5
1/2 1 2
1/5 1/2 1
 
1 1/3 1/8
3 1 1/3
8 3 1
 
1 1 3
1 1 3
1/3 1/3 1
 
1 3 4
1/3 1 1
1/4 1 1
 
1 1 1/4
1 1 1/4
4 4 1

本文较长，难免会出现各种各样的错误，欢迎评论批评指正，尊重劳动果实，转载请注明ipipblog.net

有时间的话会做一个demo放在本站的子站tools.ipipblog.net