《union find的一些改进和实现分析》——Algorithms in C++ 1-4

简介

    Union find是一种常用于集合各种操作的结构。主要包含有两个部分，一个是查找集合中是否包含有元素，另外一个是针对两个集合进行合并。这里的集合更多的是一种数学意义上的元素合集，在这么一个集合里没有重复的元素，但是根据元素之间的各种关系我们将一些元素合并到一个子集里，从而形成了上述的两个主要问题。在前面一篇图论相关的文章里已经讨论了union find的两种常用实现。这里针对它的一些优化进行细节探讨。Union find在一些集合划分，图划分的应用问题中有比较多的应用。

 

union find的两种实现

    虽然在前面的文章里已经专门抽了章节讲述了union find的定义，这里再做进一步的描述。因为union find针对的是集合。而从数学的描述来说，它们只是一组不重复的元素。从数据结构的角度来描述的话，我们有很多种选择。比如linked list, array, set等等。所以在很多具体的实现里，针对不同的场景可以选择不同的结构。我们这里针对一种比较简单的实现来讨论。

    我们知道，对于一个集合来说，最简单的方式就是定义成一个数组。里面每个下标对应集合里的每个元素，而且一开始的时候，数组里每个元素的值和下标值一样，表示它们是同一个标号。所以，针对我们查找元素和合并集合元素的时候，我们有两种实现的策略。

简单元素替换

    按照这种方式，我们每次合并一个新的元素进来的时候，都要将原来集合里所有元素的值都修改为新并入元素的值。这样做的原因在于什么呢？因为我们每次合并一个元素之后，需要有一种方式来表示这么几个合并在一起的元素。而对于这些合并在一起的元素来说，我们取他们中间哪个做代表并不重要，关键是我们随便找到它们中间的某个元素就能确定它们所在的集合标识。

    所以，我们这里的策略就是每次将新并入的元素当作这个集合的唯一标识。这样做的好处就是实现起来很简单，当然，每次更新的时候基本上要扫描一遍整个集合。一个完整的实现如下：

 public class UF {
     private int[] id;
     private int count;

     public UF(int n) {
         count = n;
         id = new int[n];
         for(int i = 0; i < n; i++)
             id[i] = i;
     }

     public int count() {
         return count;
     }

     public boolean connected(int p, int q) {
         return find(p) == find(q);
     }

     public int find(int p) {
         return id[p];
     }

     public void union(int p, int q) {
         int pId = find(p);
         int qId = find(q);

         if(pId == qId) return;

         for(int i = 0; i < id.length; i++)
             if(id[i] == pId) id[i] = qId;
         count--;
     }
 }

    它查找元素的时间复杂度非常低，只有O(1)，而合并集合元素的时候时间复杂度达到了O(N)。这种实现看起来还可以，就是感觉合并的时候似乎慢了一点，那么有没有办法使得合并的操作快点呢？

 

代表元素合并

    和前面归并元素的思路不同，这里采用的是一种类似于树的层次结构。这里的层次并不是在每个元素上面增加一个树那样的指针节点，而是在数组里，我们假定每个下标的数值表示这个元素，那么这个下标对应的元素值比如说a[1]，这里1表示元素1,而a[1]可以表示1这个元素的父节点。按照这个思路，如果我们将一个元素并入到一个集合的时候，我们可以修改这个集合的代表元素，只要这个代表元素的值为这个并入的元素就可以了。所以对于一些单独的节点或者根节点来说的话，它应该满足一点，即它本身的值和下标值是相等的。

    按照这种思路，一个实现如下：

 public class UF {
     private int[] id;
     private int count;

     public UF(int n) {
         if(n < 0)
             throw new IllegalArgumentException();
         count = n;
         id = new int[n];
         for(int i = 0; i < n; i++)
             id[i] = i;
     }

     public int count() {
         return count;
     }

     public boolean connected(int p, int q) {
         return find(p) == find(q);
     }

     public int find(int p) {
         if(p < 0 || p > id.length)
             throw new IndexOutOfBoundsException();
         while(p != id[p])
             p = id[p];
         return p;
     }

     public void union(int p, int q) {
         int pRoot = find(p);
         int qRoot = find(q);
         if(pRoot == qRoot)
             return;

         id[pRoot] = qRoot;

         count--;
     }
 }

    这种实现里，查找所在集合的代表元素需要遍历它的父节点，直到它和它的下标值相同。但是归并的时候只要修改一个元素的值就可以了。不过从最坏的情况来看，查找这个集合的根节点的时间复杂度就可能将近O(N)了。看来这个办法是使得归并的操作简单了，但是整体的时间复杂度并没有完全降下去。

    那么还有没有什么办法可以改进呢？

 

改进

    我们知道，针对后面这个合并的方法，它的问题就是在于当出现一些特殊的情况时，合并的元素和它的父节点形成了一个线性表结构，每次要去查找都要将整个表遍历一遍。问题的核心就在这里。如果有一种方法可以使得每个集合里从元素到根节点的距离尽可能的短，那么我们可以很好的改善性能。

 

weighted quick union

    这种方式就是在前面的方法上做了一个改进。我们原来每次合并集合的时候，都是固定的把一个元素的父节点设置为另外一个集合代表节点。我们知道一个集合越大，它到每个叶节点的长度就越长。如果这个时候我们再把这个大的集合的长度加长的话，只需要把它的根节点再往上延伸，也就是将它并入到另外一个集合里。而为了尽可能的保证它足够小，我们可以在两个集合合并的时候判断一下它们的大小，将小的并入到大的集合里，这样它的根路径长度就可以尽量保持得比较短。

    按照这种思路，我们实现的时候需要针对每个节点来定义以它为根节点的集合元素的多少。所以，我们需要额外再增加一个数组，专门来记录这个信息。在每次归并比较的时候，直接比较这个对应的值就可以了。而且归并之后要相应修改归并后集合根节点对应的值。

所以现在实现可以改变如下：

 public class WeightedQuickUnionUF {
     private int[] id;
     private int[] sz;
     private int count;  //表示里面集合的个数

     public WeightedQuickUnionUF(int n) {
         count = n;
         id = new int[n];
         for(int i = 0; i < n; i++) id[i] = i;  //每个元素最开始将它的父节点设置为本身
         sz = new int[n];
         for(int i = 0; i < n; i++) sz[i] = 1;  //设置每个节点对应的集合大小为1
     }

     public int count() { return count; }

     public boolean connected(int p, int q) {
         return find(p) == find(q);
     }

     public int oldFind(int p) {
         while(p != id[p]) p = id[p];
         return p;
     }

     public void union(int p, int q) {
         int i = oldFind(p);
         int j = oldFind(q);
         if(i == j) return;
         // 判断每个集合元素的大小，然后调整根节点对应的元素个数
         if(sz[i] < sz[j]) { id[i] = j; sz[j] += sz[i]; }
         else { id[j] = i; sz[i] += sz[j]; }
         count--;
     }
 }

    前面的实现代码里我们增加了一个数组int[] sz来跟踪每个元素为根节点集合的大小。然后每次合并的时候判断两个集合的大小，再将小的并入到大的集合里。

    按照前面的思路，我们输入一组集合元素关系的时候，它们归并的过程如下图：

    在前面的一些输入对如3, 8和6 1的时候，都是小的集合被作为一个子节点合并到了大的集合中。通过这种优化的方式，程序运行的时间复杂度可以达到O(logN)的效果。当然， 一般来说到了这一步，我们已经达到了一个很好的结果。实际上我们还有一个可以改进的地方，那就是path compression。

 

path compression

    对于前面的集合归并，它们很大一部分的时间是花在通过一个节点去查找它的根节点。所以从一个节点到它的根节点距离越短越好。在前面的实现中，我们可以保证每个节点到根节点的距离最多为logN。而如果我们有机会对它们的距离做进一步的压缩呢？这就是path compression的要点。因为我们每次要对两个集合合并的时候，都要通过find去查找它集合的根节点，如果每次我们在查找的过程中同时调整它到根节点的距离，使得它到根节点的距离为1,这不是更好吗？

    所以，一种典型的压缩效果应该如下图：

    当然，这种理想的情况也和我们输入的元素关系对有关系，后面会对这个关系做进一步的分析。按照前面给出的这个压缩思路，我们要修改的地方要点在于find方法，于是一种递归的压缩方法实现如下：

 public int find(int p) {
         if(p != id[p])
             id[p] = find(id[p]);
         return id[p];
     }

   这种实现比较巧妙，能够将当前节点以及从它到根节点的所有元素都设置为直接指向根节点。第一次看这个代码的实现时还颇费了点功夫，因为这一层层的递归嵌套，有时候确实比较难让人理解。我们可以按照如下的递归嵌套图来思考：

    假定我们有一个树结构的分支，从叶节点1一直到根节点4。 它们的顺序如下：

 

1--->2---->3---->4

1.p = find(1.p) --find(2)   
2.p = find(2.p)  --find(3)  
3.p = find(3.p) -- find(4)  x==3 4

    我们假定p为指向父节点的值。那么如上面所描述，每次求一个节点的父节点值的时候就需要递归到下一层，比如这里求1.p，就需要求find(2)，这样一直到find(4)。我们知道find(4)返回的结果是4。于是按照递归返回的关系就可以知道3.p = find(4)，于是得到find(3)的结果是4, 再依次返回给find(2) = 4，这样一直到最后。所以这样就保证了从叶节点到根节点这个路径上所有的节点都指向了它的根节点，同时还把根节点的值给返回了。这种实现的思路比较简练，只是有的时候不太好懂。当然，我们还可以根据前面的思路实现一个非递归版本的，就是采用一个数组来保存从叶节点到根节点的所有节点，然后将这里所有的节点都直接指向根节点。代码的实现如下：

 public int find(int p) {
     List<Integer> list = new ArrayList<Integer>();
     while(p != id[p]) {
         list.add(p);
         p = id[p];
     }
     for(Integer i : list) {
         id[i] = id[p];
     }
         return id[p];
 }

    这个实现就没什么好再说的了。

    不过还有一个比较有意思的就是在网上还有一种写法，看似可以把所有从叶节点到根节点的元素都修改了，它的实现如下：

   

 public int itFind(int p) {
         while(p != id[p]) {
             id[p] = id[id[p]];
             p = id[p];
         }
         return p;
     }

     这部分代码仔细分析的话，会发现它只是把从当前叶节点到向上每两层的节点都指向自己的祖父节点。并不是所有的都指向了根节点。在树层次不深的时候这个问题还看不出来。有兴趣的可以自己去画一下。

其他

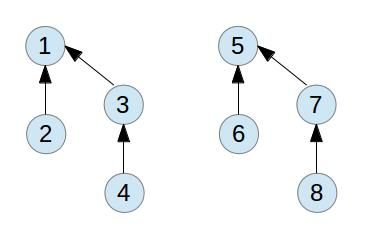
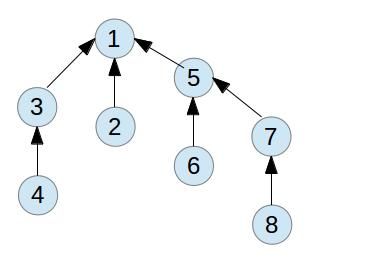
    还有一个需要说明的就是，前面提到过，我们构造的树和输入的数对也是有关系的。虽然前面的方法可以使得整个的路径得到压缩，在某些情况下，还是可以构造出最坏长度为logN的树来。比如说每次输入的数对都是两棵树的根节点，这样通过搜索从叶节点到根节点来压缩的效果就发挥不出来了。一个典型的输入如下：{ (1, 2), (3, 4) (5, 6) (7, 8), (1, 3), (5, 7), (1, 5)} 。这里按照前面的思路得到的图如下：

第一轮归并：

第二轮归并：

第三轮归并

    这是一种比较特殊的情况，虽然path compression的效果没有发挥出来，但是它可以保证最坏的情况下path的长度为logN。从概率的角度来说，毕竟这样的情况是很少见的。

 

总结

    集合的定义、查找和归并其实是一个比较值得深究的问题。虽然这里的定义实现并不复杂，但是结合一些优化手段的时候，还是有很多细节值得注意的。另外，我们有仔细思考过这种改进后的算法精确时间复杂度会有多少呢？书上给出的答案是ackerman函数的倒数。属于非常接近常数的一个量级了。不过它的推导还是非常麻烦，有时间的话再针对这个深入讨论讨论。

原文出处：http://shmilyaw-hotmail-com.iteye.com/blog/2089309