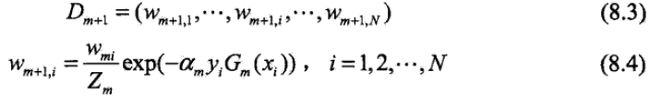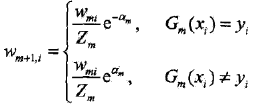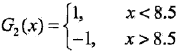提升方法 - 1 - Adaboost 算法
声明:
1,本篇为个人对《2012.李航.统计学习方法.pdf》的学习总结,不得用作商用,欢迎转载,但请注明出处(即:本帖地址)。
2,由于本人在学习初始时有很多数学知识都已忘记,所以为了弄懂其中的内容查阅了很多资料,所以里面应该会有引用其他帖子的小部分内容,如果原作者看到可以私信我,我会将您的帖子的地址付到下面。
3,如果有内容错误或不准确欢迎大家指正。
4,如果能帮到你,那真是太好了。
概述
一句话概述Adaboost算法的话就是:把多个简单的分类器结合起来形成个复杂的分类器。也就是“三个臭皮匠顶一个诸葛亮”的道理。
可能仅看上面这句话还没什么概念,那下面我引用个例子。
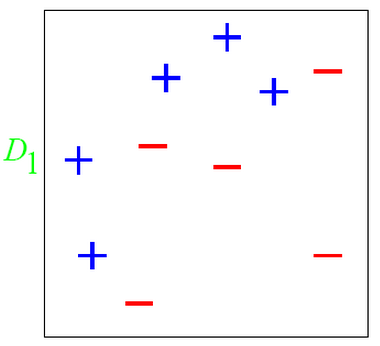
如下图所示:
在D1这个数据集中有两类数据“+”和“-”。
对于这个数据集,你会发现,不管是这么分
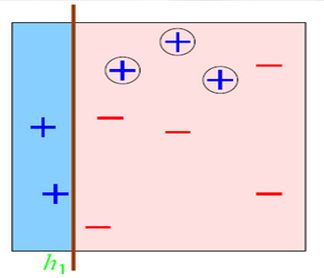
这么分
还是这么分
总有误分类点存在;
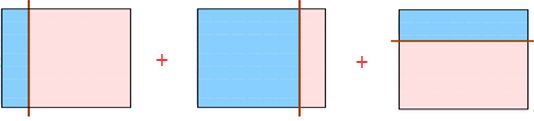
那么如果我们把上面三种分发集合起来呢?像下面这样:
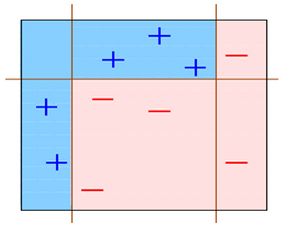
会发现把上面三个弱分类器组合起来会变成下面这个分类器:
这样一来用这个分类器就可以完美的分类数据了。
这就是Adaboost的思想。
是不是十分简单粗暴?
好,下面我们来总结下Adaboost。
Adaboost是一种迭代算法,其核心思想是针对同一训练集训练不同的分类器,即弱分类器,然后把这些弱分类请合起来,构造一个更强的最终分类器。
Adaboost算法的优点
Adaboost的优点如下:
1,Adaboost是一种有很高精度的分类器;
2,可以使用各种方法构建子分类器,Adaboost算法提供的是框架;
3,当使用简单分类器时,计算出的结果是可以理解的。而且弱分类器构造及其简单;
4,简单,不用做特征筛选;
5,不用担心过拟合(overfitting)!
Adaboost算法的步骤
通过上面的内容我们已经知道Adaboost是将多个弱分类器组合起来形成一个强分类器,那就有个问题了,我们如何训练弱分类器?我们总得用一个套路来训练,不然每次都好无章法的弄个弱分类器,那结果可能是:即使你把一万个弱分类器结合起来也没办法将数据集完全正确分类。
那么我们来进一步看看Adaboost算法的思想:
1,Adaboost给每一个训练数据添加“权值”,且最初这个权值是平均分配的。然后在之后的步骤中,提高那些被前一轮弱分类器错误分类样本的权值,并降低那些被正确分类样本的权值,这样一来,那些没有得到正确分类的数据,由于其权值的加大而受到后一轮弱分类器的更大关注
2,Adaboost给每一个弱分类器添加“权值”,且采取多数表决的方法组合弱分类器。具体地,加大分类误差率小的弱分类器的权值,使其在表决中起较大的作用;减少分类误差率大的弱分类器的权值,使其在表决中起较小的作用。
Adaboost的巧妙之处就在于它将这些想法自然且有效地实现在一种算法里。
下面来整理下Adaboost算法的步骤。
输入:
训练数据集T ={(x1, y1), (x2, y2), ..., (xN, yN)},其中xi∈X⊆Rn,yi∈Y={-1, +1};
弱学习算法。
输出:
最终分类器G(x)
解:
1,初始化训练数据的权值分布
D1= (w11, ..., w1i, ..., w1N),其中w1i= 1/N,i=1, 2, ..., N
2,对m=1, 2,..., M
a,使用具有权值分布Dm的训练数据集学习,得到基本分类器
Gm(x): X -> {-1, +1}
b,计算Gm(x)在训练数据集上的分类误差率
c,计算Gm(x)的系数
这里的对数是自然对数。
d,更新训练数据集的权值分布
这里,Zm是规范化因子
它使Dm+1成为一个概率分布。
3,构建基本分类器的线性组合
得到最终分类器
然后对上面的步骤做一些说明:
步骤1假设训练数据集具有均匀的全职分布,即每个训练样本在基本分类器的学习中作用相同。这一假设保证了第1步中能用在原始数据上学习弱分类器G1(x)。
步骤2反复学习弱分类器,在每一轮m= 1, 2, ..., M顺次地执行下列操作:
a,使用当期分布Dm加权的训练数据集,学习基本分类器Gm(x)。
b,计算基本分类器Gm(x)在加权训练数据集上的分类误差率:
这里,wmi表示第m轮中第i个实例的权值,且:
这表明,Gm(x)在加权的训练数据集上的分类误差率是被Gm(x)误分类样本的权值之和,由此可以看出数据权值分布Dm与弱分类器Gm(x)的分类误差率的关系。
c,计算弱分类器Gm(x)的系数am,am表示Gm(x)在最终分类器中的重要性。由式8.2可知,当em <= 1/2时,am >=0,并且am随em的减小而增大,所以分类误差率越小的弱分类器在最终分类器中的作用越大。
d,更新训练数据的权值分布为下一轮做准备。式8.4可以写成:
由此可知,被弱分类器Gm(x)误分类样本的权值得以扩大,而被正确分类样本的权值却得以缩小。两相比较,误分类样本的权值被放大
倍。
因此,误分类样本在下一轮学习中起更大的作用。
而,“不改变所给的训练数据,而不断改变训练数据的全职分布,使得训练数据在若分类器的学习中起不同的作用”就是Adaboost的一个特点。
步骤3中通过线性组合f(x)实现M个弱分类器的加权表决。系数am表示了弱分类器Gm(x)的重要性,这里,所有am之和并不为1。f(x)的符号决定实例x的类,f(x)的绝对值表示分类的确信度。“利用弱分类器的线性组合构建最终分类器”是Adaboost的另一个特点。
例子
给定上面这张训练数据表所示的数据,假设弱分类器由x<v或x>v产生,其阈值v使该分类器在训练数据集上的分类误差率最低,试用Adaboost算法学习一个强分类器。
解:
1,令m = 1
则初始化数据权值分布:
Dm = (wm1, wm2,..., wm10),即:D1 = (w11, w12, ..., w110)
wmi = 0.1, i = 1, 2,..., 10,即:w1i = 0.1, i = 1, 2, ..., 10
a,用下面的方式从v=1.5遍历到v=9.5
for( v=1.5;v<=9.5; v++) {
if(x < v) G1(x)=1;
elseif (x > v) G1(x) = -1;
}
并统计v取各个值使得误差率(误差率的计算方法是:所有误分类点的权值之和)。
然后发现,当v取2.5时,误分类点为x=6, 7, 8,其权值和为0.3,误差率最低,此时,当前弱分类器为:
G1(x) 在训练数据集上的误差率e1= P(G1(xi) != yi) = 0.3
b,计算G1(x)的系数:a1 =(1/2) log [(1-e1)/e1] = 0.4236
c,更新训练数据的权值分布:
D2= (w21, w22, ...,w210)
w2i= (w1i/Z1)exp(-a1yiG1(xi)),i = 1, 2,..., 10
于是
D2 = (0.0715, 0.0715, 0.0715, 0.0715,0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)
f1(x) = 0.4236G1(x)
分类器sign[f1(x)]在训练数据集上有3个误分类点。
2,令m = 2,做和上一步同上的操作。
发现在权值分布为D2的训练数据上,v = 8.5时误差率最低,此时:
当前弱分类器为:
误差率是e2 = 0.2143
a2= 0.6496
于是
权值分布为:D3 =(0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.1667, 0.1060, 0.1060, 0.1060,0.0455)
f2(x)= 0.4236G1(x) + 0.6496G2(x)
分类器sign[f2(x)]在训练数据集上有3个误分类点。
3,令m = 3。
所以在权值分布为D3的训练数据上,v =5.5时分类误差率最低,此时的弱分类器为:
G3(x)在训练样本上的误差率为e3= 0.1820
a3= 0.7514
于是
权值分布为:D4 =(0.125, 0.125, 0.125, 0.102, 0.102, 0.102, 0.065, 0.065, 0.065, 0.125)
f3(x)= 0.4236G1(x) + 0.6496G2(x) + 0.7514G3(x)
因为分类器sign[f3(x)]在训练数据集上的误分类点个数为0.
于是最终分类器为:
G(x)= sign[f3(x)] = sign[0.4236G1(x) + 0.6496G2(x)+ 0.7514G3(x)]
参考资料:
http://blog.csdn.net/haidao2009/article/details/7514787