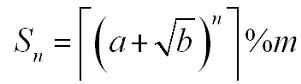hdoj 4565 So Easy! 【矩阵快速幂】【构造矩阵好题】
So Easy!Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 3243 Accepted Submission(s): 1046
Problem Description
A sequence S
n is defined as:
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S n. You, a top coder, say: So easy! 
Input
There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2
15, (a-1)
2< b < a
2, 0 < b, n < 2
31.The input will finish with the end of file.
Output
For each the case, output an integer S
n.
Sample Input
Sample Output
|
定义——┌3.14┐=4
题意：给你a、b、n、m，让你求出
分析：(a + sqrt(b)) ^ n + (a - sqrt(b)) ^ n = C[n]，由于共轭的性质，C[n]一定是整数。
又由题中约束条件(a-1)^2 < b < a^2 —— (a - sqrt(b)) ^ n < 1，这样就有公式┌(a+sqrt(b)) ^ n┐= C[n]。
C[n] = (a+sqrt(b)) ^ n + (a - sqrt(b)) ^ n
——C[n-1] * 2*a = (a + sqrt(b)) ^ (n-1) + (a - sqrt(b)) ^ (n-1) * (a + sqrt(b) + a - sqrt(b))
——C[n-1] * 2*a = (a + sqrt(b)) ^ n + (a - sqrt(b)) ^ n + (a + sqrt(b)) ^ (n-2) + (a - sqrt(b)) ^ (n-2) * (a + sqrt(b)) * (a -sqrt(b))
——C[n-1] * 2*a = C[n] + C[n-2] * (a^2-b)
得—— C[n] = C[n-1] * 2 * a - C[n-2] * (a^2 - b)。
又知道C[0] = 2, C[1] = 2 * a。
下面构建好矩阵就可以KO了。
注意计算过程中负数的处理！
AC代码：
#include <cstdio>
#include <cstring>
#include <algorithm>
#define LL long long
using namespace std;
struct Matrix {
LL a[2][2];
};
Matrix ori, res;
LL F[2];
void init(LL a, LL b, LL m)
{
memset(ori.a, 0, sizeof(ori.a));
memset(res.a, 0, sizeof(res.a));
res.a[0][0] = res.a[1][1] = 1;
ori.a[1][0] = 1;
ori.a[1][1] = 2*a%m;
ori.a[0][1] = -(a*a-b)%m;
F[0] = 2%m; F[1] = 2*a%m;
}
Matrix multi(Matrix x, Matrix y, LL m)
{
Matrix z;
memset(z.a, 0, sizeof(z.a));
for(int i = 0; i < 2; i++)
{
for(int k = 0; k < 2; k++)
{
if(x.a[i][k] == 0) continue;
for(int j = 0; j < 2; j++)
z.a[i][j] = (z.a[i][j] + (x.a[i][k] * y.a[k][j])%m + m)%m;
}
}
return z;
}
void solve(LL n, LL m)
{
while(n)
{
if(n & 1)
res = multi(ori, res, m);
ori = multi(ori, ori, m);
n >>= 1;
}
LL ans = (res.a[0][1] * F[0] % m + res.a[1][1] * F[1] % m + m)%m;
printf("%lld\n", ans);
}
int main()
{
LL a, b, n, m;
while(scanf("%lld%lld%lld%lld", &a, &b, &n, &m) != EOF)
{
if(n == 1)
{
printf("%lld\n", 2*a%m);
continue;
}
init(a, b, m);
solve(n-1, m);
}
return 0;
}