opencv各种滤波分析bilateralFilter、Laplacian、bitwise_and和GaussianBlur

我们首先来看一下bilateralFilter，双边滤波

具体查看：https://en.wikipedia.org/wiki/Bilateral_filter点击打开链接

A bilateral filter is a non-linear, edge-preserving and noise-reducing smoothing filter for images. The intensity value at each pixel in an image is replaced by a weighted average of intensity values from nearby pixels. This weight can be based on a Gaussian distribution. Crucially, the weights depend not only on Euclidean distance of pixels, but also on the radiometric differences (e.g. range differences, such as color intensity, depth distance, etc.). This preserves sharp edges by systematically looping through each pixel and adjusting weights to the adjacent pixels accordingly.

也就是说：双边滤波器是一种非线性，边缘保留和减除噪声的图像平滑滤波器。在图像的每个像素强度值处被从附近的像素强度值的加权平均来取代。这个权值可以是基于高斯分布的。关键的是，权重不仅取决于像素的欧几里得距离,而且也在辐射差异（比如，范围的差异，颜色强度，深度距离等）。这个在系统地遍历每个像素的过程中保留了锐利的边缘和相应调整相邻的像素的权重。

The bilateral filter is defined as双边滤波器的定义如下：

where the normalization term标准化的术语：

ensures that the filter preserves image energy and

•  is the filtered image;过滤后的图像
•  is the original input image to be filtered;原始输入图像
•  are the coordinates of the current pixel to be filtered;当前正在过滤的像素的坐标
•  is the window centered in ;过滤窗口的中心
•  is the range kernel for smoothing differences in intensities. This function can be a Gaussian function;内核范围平滑强度的差异，这个函数是高斯函数
•  is the spatial kernel for smoothing differences in coordinates. This function can be a Gaussian function;是平滑的内核空间坐标的差异，这个函数也是高斯函数

As mentioned above, the weight  is assigned using the spatial closeness and the intensity difference.^[1] Consider a pixel located at  which needs to be denoised in image using its neighbouring pixels and one of its neighbouring pixels is located at . Then, the weight assigned for pixel  to denoise the pixel  is given by: 

where σ_d and σ_r are smoothing parameters and I(i, j) and I(k, l) are the intensity of pixels  and  respectively. After calculating the weights, normalize them. 

where  is the denoised intensity of pixel .

也就是说：权重指定使用空间的亲密度和强度差异。

参数：

• As the range parameter σ_r increases, the bilateral filter gradually approaches Gaussian convolution more closely because the range Gaussian widens and flattens, which means that it becomes nearly constant over the intensity interval of the image.
• As the spatial parameter σ_d increases, the larger features get smoothened.

随着参数σr范围增加，双边滤波器逐渐接近高斯卷积更密切,因为高斯范围扩大并趋于平稳，这意味着它变得几乎恒定强度的图像的时间间隔。

随着空间参数σd增加,得到更大的平滑特性。

限制：

The bilateral filter in its direct form can introduce several types of image artifacts:

• Staircase effect - intensity plateaus that lead to images appearing like cartoons 阶梯效应-强度高原导致出现像卡通图片
• Gradient reversal - introduction of false edges in the image 梯度逆转-在图像中引入虚假边缘

There exist several extensions to the filter that deal with these artifacts. Alternative filters, like the guided filter ，have also been proposed as an efficient alternative without these limitations.存在几个扩展过滤器处理这些工件，选择过滤器,如引导过滤器,也被建议作为一种有效的替代没有这些限制

相关模型：

The Bilateral filter was shown to be an application of the short time kernel of the Beltrami flow .See also.双边滤波器被证明是短时间的应用程序内核的贝尔特拉米流

With similar goal as the Bilateral filter, the class of edge-preserving smoothing filters also includes: Anisotropic Diffusion, the Weighted Least Squares framework,the Edge-Avoiding Wavelets,Geodesic editing,Guided filtering,and the Domain Transform framework.

GaussianBlur ：高斯模糊

具体查看：https://en.wikipedia.org/wiki/Gaussian_blur 点击打开链接

A Gaussian blur (also known as Gaussian smoothing) is the result of blurring an image by a Gaussian function. It is a widely used effect in graphics software, typically to reduce image noise and reduce detail. The visual effect of this blurring technique is a smooth blur resembling that of viewing the image through a translucent screen, distinctly different from the bokeh effect produced by an out-of-focus lens or the shadow of an object under usual illumination. Gaussian smoothing is also used as a pre-processing stage in computer vision algorithms in order to enhance image structures at different scales—see scale space representation and scale space implementation.

Mathematically, applying a Gaussian blur to an image is the same as convolving the image with a Gaussian function. This is also known as a two-dimensional Weierstrass transform. By contrast, convolving by a circle (i.e., a circularbox blur) would more accurately reproduce the bokeh effect. Since the Fourier transform of a Gaussian is another Gaussian, applying a Gaussian blur has the effect of reducing the image's high-frequency components; a Gaussian blur is thus a low pass filter.

Mechanics：

The Gaussian blur is a type of image-blurring filter that uses a Gaussian function (which also expresses the normal distribution in statistics) for calculating the transformation to apply to each pixel in the image. The equation of a Gaussian function in one dimension is

in two dimensions, it is the product of two such Gaussians, one in each dimension:

^{[1] [2]}

where x is the distance from the origin in the horizontal axis, y is the distance from the origin in the vertical axis, and σ is the standard deviation of the Gaussian distribution. When applied in two dimensions, this formula produces a surface whose contours are concentric circles with a Gaussian distribution from the center point. Values from this distribution are used to build a convolution matrix which is applied to the original image. Each pixel's new value is set to a weighted average of that pixel's neighborhood. The original pixel's value receives the heaviest weight (having the highest Gaussian value) and neighboring pixels receive smaller weights as their distance to the original pixel increases. This results in a blur that preserves boundaries and edges better than other, more uniform blurring filters; see also scale space implementation.

Laplacian ：拉普拉斯算子

Laplacian 算子是n维欧几里德空间中的一个二阶微分算子，定义为梯度grad（）的散度div（）。因此如果f是二阶可微的实函数，则f的拉普拉斯算子定义为：

(1) f的拉普拉斯算子也是笛卡儿坐标系xi中的所有非混合二阶偏导数求和：

(2) 作为一个二阶微分算子，拉普拉斯算子把C函数映射到C函数，对于k ≥ 2。表达式(1)（或(2)）定义了一个算子Δ : C(R) → C(R)，或更一般地，定义了一个算子Δ : C(Ω) → C(Ω)，对于任何开集Ω。

对于阶跃状边缘，魂不附体导数在边缘点出现零交叉，即边缘点两旁二阶导数取异号。据此，对数字图像{f（i，j）}的每个像素，取它关于x轴方向和y轴方向的二阶差分之和，表示为

函数的拉普拉斯算子也是该函数的黑塞矩阵的迹,可以证明，它具有各向同性，即与坐标轴方向无关，坐标轴旋转后梯度结果不变。如果邻域系统是4 邻域，Laplacian 算子的模板为：

0	1	0
1	-4	1
0	1	0

如果邻域系统是8 邻域，Laplacian 算子的模板为：

1	1	1
1	-8	1
1	1	1

前面提过，Laplacian 算子对噪声比较敏感，所以图像一般先经过平滑处理，因为平滑处理也是用模板进行的，所以，通常的分割算法都是把Laplacian 算子和平滑算子结合起来生成一个新的模板。

bitwise_and：

具体查看：https://en.wikipedia.org/wiki/Bitwise_operation点击打开链接

代码：

#include "cv.h"
#include "highgui.h"
using namespace cv;
using namespace std;
int main()
{
string name="D:\\VC98\\C++项目\\opencv\\cv_Laplacian\\cv_Laplacian\\f.jpg";
Mat src1=imread(name,1);//读入图像矩阵
Mat img;
//双边滤波，第3个参数d可以说d>5时不能实时处理，最后两个参数是sigma参数，一般相同，
//<10时基本没效果, >150时漫画效果
bilateralFilter(src1,img,5,150,150);
bilateralFilter(img,src1,5,150,150);
//img.copyTo(src1);

cvNamedWindow("bilateral",0);
imshow("bilateral",src1);
// waitKey(0);

Mat src;
cvtColor(src1,src,CV_BGR2GRAY);
//粗线，越大越粗，但是会有大量噪点
Mat imgL;
//第三个参数ddepth表示目标图像的深度，ddepth=-1时，与原图像一致
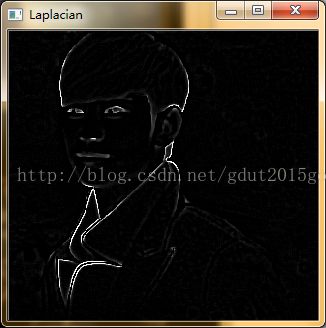
Laplacian(src,imgL,-1,3,1);
cvNamedWindow("Laplacian",0);
imshow("Laplacian",imgL);
// waitKey(0);
//细线
Mat imgC;
Canny(src,imgC,30,90);
cvNamedWindow("Canny",0);
imshow("Canny",imgC);
// waitKey(0);

Mat imgS,imgSx,imgSy,imgS0;
Sobel(src,imgSx,-1,0,1);
Sobel(src,imgSx,-1,1,0);
imgS=imgSx+imgSy;
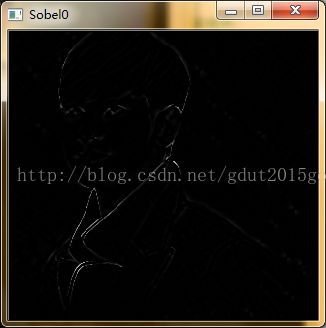
Sobel(src,imgS0,-1,1,1);
cvNamedWindow("Sobel0",0);
cvNamedWindow("Sobel",0);
imshow("Sobel0",imgS0);
imshow("Sobel",imgS);
// waitKey(0);

Mat imgTotal;
imgTotal=imgC+imgS+imgL;
//imgTotal.convertTo(imgTotal,CV_32FC1);
normalize(imgTotal,imgTotal,255,0,CV_MINMAX);
GaussianBlur(imgTotal,imgTotal,Size(3,3),3);
threshold(imgTotal,imgTotal,100,255,THRESH_BINARY_INV);
cvNamedWindow("Total",0);
imshow("Total",imgTotal);
// waitKey(0);

Mat imgTotalC3;
cvtColor(imgTotal,imgTotalC3,CV_GRAY2BGR);
bitwise_and(src1,imgTotalC3,src1);
cvNamedWindow("Result",0);
imshow("Result",src1);
waitKey(0);

name.insert(11,"_edge");
imwrite(name,src1);

}

结果：

原图：

bilateral：

Laplacian：

Canny：

Sobel0：

Sobel：

Total：

Result：