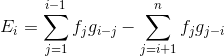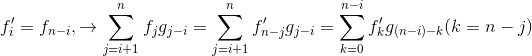bzoj3527 力 fft
bzoj上面没有题面,这里给一个吧。题面:
样例输入输出:
注意到等号左边是一个卷积的形式(什么是卷积?可以看成是多项式乘法),然后发现右边只需要把f数组反一下就变成就卷积的形式了,具体的:
因此左右两边都化成了卷积的形式,就可以做两边多项式乘法来得到结果了。用fft加速到O(NlogN)。
以前fft都是用递归版的(就写了一遍还好意思用“都”),现在发现蝴蝶变换好像也还是蛮简单的嘛,那就在这里讲一下吧。。~\(≧▽≦)/~(不用蝴蝶变换算导上面的还是很清楚的,不过蝴蝶变换我以前学的时候没看懂)
注意到对于某一段(i,j),所有在偶数位的都会并入(i,mid),而奇数位的并入(mid+1,j),那么就相当于对应的二进制位为0的并到左边,为1的并到右边。那么对于原始的数列,二进制最后一位为0的在左半区间,为1的在右半区间;第二位为0的在所在的半区间的左半区间。。。然后就可以得到某一位i最后变到哪一个位置了(实际上就是二进制倒过来?),然后再操作的时候变回来就行了。
AC代码如下:
#include<cstdio>
#include<iostream>
#include<cmath>
#define pi acos(-1.0)
#define N 400000
using namespace std;
struct cpx{ double r,i; }a[N],b[N];
int n,m,pos[N]; double f[N],g[N],ans[N];
cpx operator +(cpx x,cpx y){ x.r+=y.r; x.i+=y.i; return x; }
cpx operator -(cpx x,cpx y){ x.r-=y.r; x.i-=y.i; return x; }
cpx operator *(cpx x,cpx y){
cpx z; z.r=x.r*y.r-x.i*y.i; z.i=x.r*y.i+x.i*y.r; return z;
}
void dft(cpx *a,int p){
int i,j,k; cpx wn,w,u,v;
for (k=2; k<=m; k<<=1){
wn.r=cos(pi*2.0/k*p); wn.i=sin(pi*2.0/k*p);
for (i=0; i<m; i+=k){
int mid=k>>1; w.r=1; w.i=0;
for (j=i; j<i+mid; j++){
u=a[j]; v=a[j+mid]*w;
a[j]=u+v; a[j+mid]=u-v; w=w*wn;
}
}
}
if (p<0) for (i=0; i<m; i++) a[i].r/=m;
}
void fft(){
int i,k;
for (i=0; i<m; i++){
k=pos[i]; a[k].i=b[k].i=0;
a[k].r=f[i]; b[k].r=g[i];
}
dft(a,1); dft(b,1); for (i=0; i<m; i++) b[i]=a[i]*b[i];
for (i=0; i<m; i++) a[pos[i]]=b[i];
dft(a,-1);
}
int main(){
scanf("%d",&n); m=n<<1|1; int i,j,k=0,cnt=0;
for (i=1; i<m; i<<=1) cnt++; m=i;
for (i=0; i<m; i++)
for (k=i,j=cnt; j; j--,k>>=1) pos[i]=pos[i]<<1|(k&1);
for (i=1; i<=n; i++){
scanf("%lf",&f[i]); g[i]=1.0/i/i;
}
fft(); for (i=1; i<=n; i++) ans[i]=a[i].r;
for (i=0; i*2<n; i++) swap(f[i],f[n-i]);
fft();
for (i=1; i<=n; i++) printf("%.3f\n",ans[i]-a[n-i].r);
return 0;
}
by lych
2016.3.9