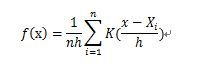R语言与非参数统计（核密度估计）
R语言与非参数统计（核密度估计）
核密度估计是在概率论中用来估计未知的密度函数，属于非参数检验方法之一，由Rosenblatt (1955)和Emanuel Parzen(1962)提出，又名Parzen窗（Parzen window）。
假设我们有n个数X1-Xn,我们要计算某一个数X的概率密度有多大。核密度估计的方法是这样的：
其中K为核密度函数,h为设定的窗宽。
核密度估计的原理其实是很简单的。在我们对某一事物的概率分布的情况下。如果某一个数在观察中出现了，我们可以认为这个数的概率密度很大，和这个数比较近的数的概率密度也会比较大，而那些离这个数远的数的概率密度会比较小。基于这种想法，针对观察中的第一个数，我们都可以f(x-xi)去拟合我们想象中的那个远小近大概率密度。当然其实也可以用其他对称的函数。针对每一个观察中出现的数拟合出多个概率密度分布函数之后，取平均。如果某些数是比较重要，某些数反之，则可以取加权平均。
但是核密度的估计并不是，也不能够找到真正的分布函数。我们可以举一个极端的例子：在R中输入：
plot(density(rep(0, 1000)))
可以看到它得到了正态分布的曲线，但实际上呢？从数据上判断，它更有可能是一个退化的单点分布。
但是这并不意味着核密度估计是不可取的，至少他可以解决许多模拟中存在的异方差问题。比如说我们要估计一下下面的一组数据：
set.seed(10) dat<-c(rgamma(300,shape=2,scale=2),rgamma(100,shape=10,scale=2))
可以看出它是由300个服从gamma（2,2）与100个gamma（10,2）的随机数构成的，他用参数统计的办法是没有办法得到一个好的估计的。那么我们尝试使用核密度估计：
plot(density(dat),ylim=c(0,0.2))
将利用正态核密度与标准密度函数作对比
dfn<-function(x,a,alpha1,alpha2,theta){
a*dgamma(x,shape=alpha1,scale=theta)+(1-a)*dgamma(x,shape=alpha2,scale=theta)}
pfn<-function(x,a,alpha1,alpha2,theta){
a*pgamma(x,shape=alpha1,scale=theta)+(1-a)*pgamma(x,shape=alpha2,scale=theta)}
curve(dfn(x,0.75,2,10,2),add=T,col="red")
得到下图：
（红色的曲线为真实密度曲线）
可以看出核密度与真实密度相比，得到大致的估计是不成问题的。至少趋势是得到了的。如果换用gamma分布的核效果无疑会更好，但是遗憾的是r中并没有提供那么多的核供我们挑选（其实我们知道核的选择远没有窗宽的选择来得重要），所以也无需介怀。
R中提供的核：kernel = c("gaussian", "epanechnikov", "rectangular", "triangular", "biweight","cosine", "optcosine")。
我们先来看看窗宽的选择对核密度估计的影响：
dfn1<-function(x){ 0.5*dnorm(x,3,1)+0.5*dnorm(x,-3,1)} par(mfrow=c(2,2)) curve(dfn1(x),from=-6,to=6) data<-c(rnorm(200,3,1),rnorm(200,-3,1)) plot(density(data,bw=8)) plot(density(data,bw=0.8)) plot(density(data,bw=0.08))
得到下图，我们可以清楚的看到带宽为0.8恰好合适，其余的不是拟合不足便是过拟合。
窗宽究竟该如何选择呢？
我们这里不加证明的给出最佳窗宽选择公式：
(这个基于积分均方误差最小的角度得到的)
这里介绍两个可操作的窗宽估计办法：(这两种方法都比较容易导致过分光滑)
1、 Silverman大拇指法则
这里使用R(phi’’)/sigma^5估计R（f’’），phi代表标准正态密度函数，得到h的表达式：
h=(4/(3n))^(*1/5)*sigma
2、 极大光滑原则
h=3*(R(K)/(35n))^(1/5)*sigma
当然也有比较麻烦的窗宽估计办法，比如缺一交叉验证，插入法等，可以参阅《computational statistics》一书
我们用上面的两种办法得到的窗宽是多少，他的核密度估计效果好吗？
我们还是以上面的混合正态数据为例来看看效果。
使用大拇指法则，将数据n=400,sigma=3.030658,带入公式，h=0.9685291
使用极大光滑原则，假设K为正态核，R(K)=1/(sqrt(2*pi))，h=1.121023
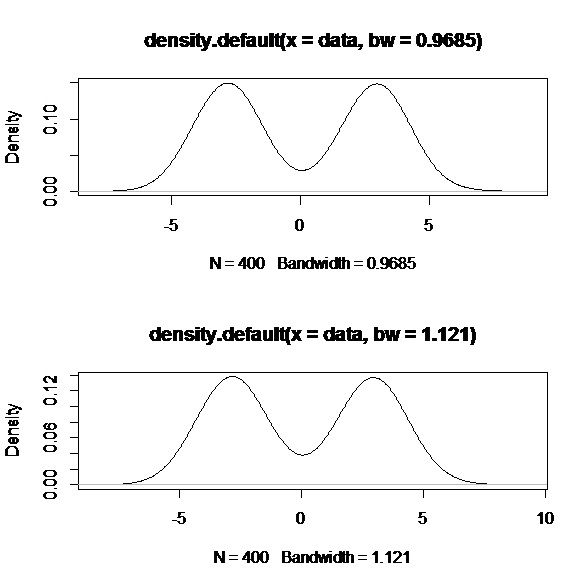
可以看出他们都比我们认为的h=0.8要大一些，作图如下：
plot(density(data,bw=0.9685)) plot(density(data,bw=1.1210))
由我们给出的
以Gauss核为例做核密度估计
用Gauss核做核密度估计的R程序如下（还是使用我们的混合正态密度的例子）：
ker.density=function(x,h){
x=sort(x)
n=length(x);s=0;t=0;y=0
for(i in 2:n)
s[i]=0
for(i in 1:n){
for(j in 1:n)
s[i]=s[i]+exp(-((x[i]-x[j])^2)/(2*h*h))
t[i]=s[i]
}
for(i in 1:n)
y[i]=t[i]/(n*h*sqrt(2*pi))
z=complex(re=x,im=y)
hist(x,freq=FALSE)
lines(z)
}
ker.density(data,0.8)
作图如下：
最后说一个R的内置函数density（）。其实我觉得如果不是为了简要介绍核密度估计的一些常识我们完全可以只学会这个函数
先看看函数的基本用法：
density(x, ...)
## Default S3 method:
density(x, bw = "nrd0", adjust = 1,
kernel = c("gaussian", "epanechnikov", "rectangular",
"triangular", "biweight",
"cosine", "optcosine"),
weights = NULL, window = kernel, width,
give.Rkern = FALSE,
n = 512, from, to, cut = 3, na.rm = FALSE, ...)
对重要参数做出较为详细的说明：
X:我们要进行核密度估计的数据
Bw:窗宽，这里可以由我们自己制定，也可以使用默认的办法nrd0: Bandwidth selectors for Gaussian kernels。我们还可以使用bw.SJ(x,nb = 1000, lower = 0.1 * hmax, upper = hmax, method = c("ste","dpi"), tol = 0.1 * lower)，这里的method =”dpi”就是前面提到过的插入法，”ste”代表solve-the-equationplug-in，也是插入法的改进
Kernel：核的选择
Weights:对比较重要的数据采取加权处理
对于上述混合正态数据data，有
> density(data)
Call:
density.default(x = data)
Data: data (400 obs.); Bandwidth 'bw' = 0.8229
x y
Min. :-7.5040 Min. :0.0000191
1stQu.:-3.5076 1st Qu.:0.0064919
Median : 0.4889 Median :0.0438924
Mean :0.4889 Mean :0.0624940
3rdQu.: 4.4853 3rd Qu.:0.1172919
Max. :8.4817 Max. :0.1615015
知道带宽：h=0.8229（采取正态密度核）那么带入密度估计式就可以写出密度估计函数。
最后以faithful数据集为例说明density的用法：
R数据集faithful是old faithful火山爆发的数据，其中“eruption”是火山爆发的持续时间，waiting是时间间隔
对数据“eruption”做核密度估计
R程序：
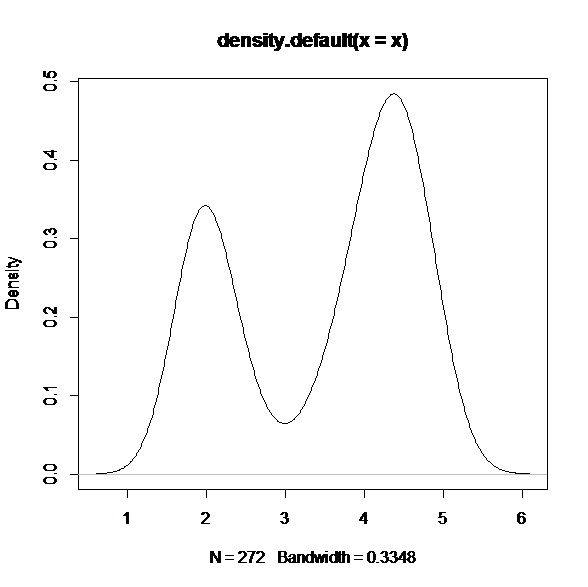
data(faithful) A<-faithful x<-A[,"eruptions"] density(x) plot(density(x))
知道h= 0.3348
作图：
关于核密度估计R中还有不少函数包提供了大量的支持：
ks Kernel smoothing
|