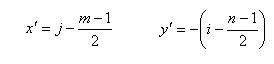机器视觉学习
1. 坐标系:
透视投影(perspective projection): 以摄像机为原点, 建立oxyz坐标系, 为了避免图像倒立, 将像平面平移到场景与坐标xy平面中间的位置, 距离坐标xy平面为焦距f, 形成图像平面。
z轴跟光轴重合。
点在图像平面中的位置由下式给出:
正交投影(orthogonal projection):
用平行于光轴的光将场景投射到图像平面上, 因此也称为平行投影(parallel projection), 是透视投影的特例(焦距f无穷大)。
在计算机视觉系统中涉及到以下几种坐标:
l 像素坐标:表示图像阵列中图像像素的位置i, j;
l 图像平面坐标:表示场景点在图像平面上的投影xp, yp;
l 摄象机坐标:即以观察者为中心的坐标,将场景点表示成以观察者为中心的数据形式x,y.
l 场景坐标:也称作绝对坐标(或世界坐标),用于表示场景点的绝对坐标X,Y;
摄像机主点,即光轴与图像平面的交点
像素坐标: 对应于图像像素。 本为整数, 可用子像素扩展。 原点在左上角, i指向下方, j指向右方。
像素坐标到图像坐标的转换为:
考虑像素平面的行列间距相等时:
考虑行距为sx, 列距为sy:
由于在许多情况下,图像平面坐标系是摄象机坐标系的一部分,因此,为了书写简单,在不混淆的情况下,通常使用摄象机平面坐标x-y代替图像平面坐标xp-yp。
二值化:
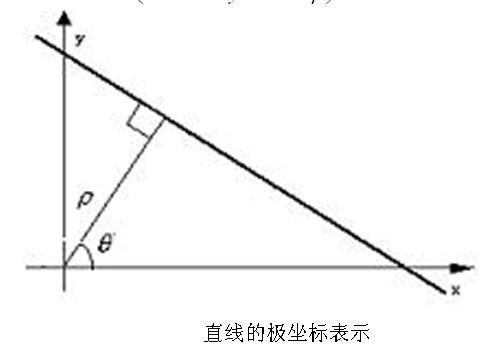
二值图像分析是指把图像按照0,1两个灰度进行阀值化处理。 假定摄像机位置, 背景, 环境等都是已知, 这种识别通常还需要需要识别物体的尺寸, 位置, 方向, 密集比, 体态比等。面积用像素值求和。位置用矩心表示。 方向用长轴表示(对于圆, 不唯一)物体的方向。 二维平面上与最小惯量轴同方向的最小二阶矩轴被定为长轴。 图像中物体的二阶矩轴是这样一条线,物体上的全部点到该线的距离平方和最小。给出一幅二值图像 ,计算物体点到直线的最小二乘方拟合,使所有物体点到直线的距离平方和最小。直线通常用极坐标表示:
这里x, y是直线上的点。方程可通过三角形相似求的。
则物体上的任何点到该直线的距离为:
这里, x, y表示物体上的任何点。方程可通过三角形相似求的。
其它关系, 通过下面的图表示:
通过对最小二乘方拟合的表达式求极小值(对直线到原点的距离求导), 最终可得到惯性轴的方向:
伸长率(最短的和最长的比):
具体要参见相应的文档。
密集比:面积与周长的平方的比值。园最密。 等周长时, 正方形比长方形密。
体态比定义为区域的最小外接矩形的长与宽之比,正方形和圆的体态比等于1,细长形物体的体态比大于1