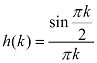小波与滤波器组（1）

低通滤波器（Lowpass Filter）的目的是移除差异保留平均，也就是移除高频保留低频，这个是一个比较直观的定义。利用数学公式进行解释就是，假设L={l(n)}是一个低频滤波器组，如果对L中的所有元素进行累加操作得到的结果不等于0，那么就说L是一个低通滤波器，大多数情况下累加操作的结果等于1。,高通滤波器刚好和低通滤波器相反——为了移除平均而保留差异，也就是说移除低频保留高频。在数学上的解释就是，假设H={h(n)}是一个高频滤波器组，如果对H中的所有元素进行累加操作得到的结果刚好等于0。

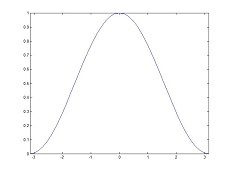
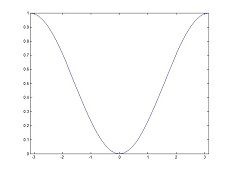
根据数学上的定义，Y=X*Z，在一定条件下可以得到X=Y/Z。假设这里的X是一个图像，Z是一个滤波器，Y作为一个滤波器的结果是否满足上面的逆变换呢？答案显然是否定的。因为可以进行逆变换的条件是Z不等于0。诚然，当L={1/4，1/2，1/4}的时候，作为一个低通滤波器数值上的确是不等于0的。然而这只是说他在空间域上不等于0。下面看这个低频滤波器在频率域的图形（左图）以及对应的H={-1/4，1/2，-1/4}的频率域的图形（右图）。这两个图形的很容易通过手工就算出来，滤波器的进行傅里叶变换就可以了，或者通过matlab函数psf2otf也可以得到结果。从频率域来看，两个滤波器都经过了零点，这样经过滤波器处理后的图像就不能直接利用上面的公式进行逆变换，也就是说滤波之后的图像不能恢复。

通过上面的分析可以知道，单个滤波器滤波之后不能对图像进行恢复，那么处理之后，就不能对图像进行重建。既然一个滤波器滤波之后不能进行重建，那么两个滤波器组合呢？比如利用高频滤波器得到高频部分，利用低频滤波器得到低频部分不就可以重构了吗？上面只是理论上可以这样做，但是想要达到重建的效果，还需要一些额外的问题需要解决。

1 怎样去重建信号，按照上面的理论得到高频和低频信号之后怎么让着两组信号组合成一个信号？

2 怎样找到这样的滤波器？

3 怎样减少存储和计算量？

4 将信号分解的目标是为了进行处理，分解之后这些信号具备什么样的性质？

根据上面的思路，假设有一个低频滤波器组满足低通滤波器刚好让所有的低频信号能够完整的通过，而高通滤波器则刚好能够让高频信号通过；那么经过滤波器组处理之后得到的结果直接相加就可以重建原来的信号。则满足上面要求的滤波器形式的傅里叶变换应该满足下图中的等式：

   

其中右边的图为低通滤波器的傅里叶变换，而右边的图为高通滤波器的傅里叶变换。对于低通滤波器而言，只需要满足下列等式就可以了

，而高通滤波器则只需要将上面的h(k)平移一个pi相位就可以了。上面提到的找滤波器的问题貌似解决了，然而，通过观察滤波器组的傅里叶变换等式可知，h（k）的取值是整个整数序列，也就是说滤波器组中的滤波器是无穷的，如果滤波器不是无穷的则会出现Gibbs现象。很明显这种滤波器是不可得的，因此上面滤波器组中的滤波器被称之为理想滤波器。

因为，不能够构造一个理想低通滤波器。通过计算可以知道

。实际上这个公式表明理想低通滤波器和理想高通滤波器都是半带滤波器，高通滤波器能够通过低通滤波器平移一个PI相位得到