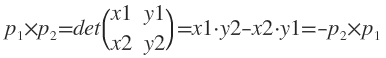hdu1086 You can Solve a Geometry Problem too

You can Solve a Geometry Problem too

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 9306    Accepted Submission(s): 4563

Problem Description

Many geometry（几何）problems were designed in the ACM/ICPC. And now, I also prepare a geometry problem for this final exam. According to the experience of many ACMers, geometry problems are always much trouble, but this problem is very easy, after all we are now attending an exam, not a contest :)
Give you N (1<=N<=100) segments（线段）, please output the number of all intersections（交点）. You should count repeatedly if M (M>2) segments intersect at the same point.

Note:
You can assume that two segments would not intersect at more than one point. 

 

Input

Input contains multiple test cases. Each test case contains a integer N (1=N<=100) in a line first, and then N lines follow. Each line describes one segment with four float values x1, y1, x2, y2 which are coordinates of the segment’s ending. 
A test case starting with 0 terminates the input and this test case is not to be processed.

 

Output

For each case, print the number of intersections, and one line one case.

 

Sample Input

   
   
   
   

    
    
    
    2
0.00 0.00 1.00 1.00
0.00 1.00 1.00 0.00
3
0.00 0.00 1.00 1.00
0.00 1.00 1.00 0.000
0.00 0.00 1.00 0.00
0
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    1
3
   
   
   
   

        题意是计算线段交点数量，不用舍去重复交点。。。水题一A，刚开始是想着联立方程组解直线方程，然后看解出来的（x, y）是不是在两条直线的x和y的区间上，后来感觉这么写太长，上网看了看用叉乘积和向量做挺简洁。。。整理一下

直接解方程判点在不在线段区间上

#include <cstdio>
#include <iostream>
#include <cmath>

using namespace std;

const double LIMIT = 1e-8;

typedef struct {
	double x, y;
}point;

typedef struct {
	point p1;
	point p2;
}line;

line L[15];

void Swap(double &a, double &b) {  //给a,b交换排序，好判断点是否在区间内
	if (a > b) {
		double tem = a;
		a = b;
		b = tem;
	}
}

bool IsItersect(line l1, line l2) {
	//两直线平行且垂直于相同坐标轴
	if (fabs(l1.p1.x - l1.p2.x) < LIMIT && fabs(l2.p1.x - l2.p2.x) < LIMIT || \
		fabs(l1.p1.y - l1.p2.y) < LIMIT && fabs(l2.p1.y - l2.p2.y) < LIMIT) {
		return false;
	}
	//垂直于不同的坐标轴，应该再判断下交点有没有在线段上，这都过了，数据是有多水
	if (fabs(l1.p1.x - l1.p2.x) < LIMIT && fabs(l2.p1.y - l2.p2.y) < LIMIT || \
		fabs(l1.p1.y - l1.p2.y) < LIMIT && fabs(l2.p1.x - l2.p2.x) < LIMIT) {
		return true;
	}
	double k1 = (l1.p1.y - l1.p2.y) / (l1.p1.x - l1.p2.x);  //斜率存在，计算斜率
	double k2 = (l2.p1.y - l2.p2.y) / (l2.p1.x - l2.p2.x);
	if (fabs(k1 - k2) < LIMIT)  //斜率相等，平行
		return false;
	double b1 = l1.p1.y - k1 * l1.p1.x;
	double b2 = l2.p1.y - k2 * l2.p1.x;
	double x0 = (b2 - b1) / (k1 - k2);    //解出x0, y0为交点
	double y0 = k1 * x0 + b1;
	Swap(l1.p1.x, l1.p2.x);
	Swap(l2.p1.x, l2.p2.x);
	Swap(l1.p1.y, l1.p2.y);
	Swap(l2.p1.y, l2.p2.y);
	//看交点是否在线段上，好长( -_-) ! 
	if (x0 > l1.p1.x && x0 < l1.p2.x && x0 > l2.p1.x && x0 < l2.p2.x \
		&& y0 > l1.p1.y && y0 < l1.p2.y && y0 > l2.p1.y && y0 < l2.p2.y \
		|| fabs(x0 - l1.p1.x) < LIMIT && fabs(y0 - l1.p1.y) < LIMIT || \
		fabs(x0 - l1.p2.x) < LIMIT && fabs(y0 - l1.p2.y) < LIMIT \
		|| fabs(x0 - l2.p1.x) < LIMIT && fabs(y0 - l2.p1.y) < LIMIT || \
		fabs(x0 - l2.p2.x) < LIMIT && fabs(y0 - l2.p2.y) < LIMIT)
		return true;
	else
		return false;
}

int main()
{
	int N;
	while (~scanf("%d", &N) && N) {
		for (int i = 0; i < N; i++) {
			scanf("%lf%lf%lf%lf", &L[i].p1.x, &L[i].p1.y, &L[i].p2.x, &L[i].p2.y);
		}
		int cou = 0;
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				if (i != j) {
					if (IsItersect(L[i], L[j]))
						cou++;
				}
			}
		}
		printf("%d\n", cou / 2);
	}
	return 0;
}

用向量和叉乘积

引用下别人的博客里的东西

来源：http://www.cnblogs.com/zhangchaoyang/articles/2668562.html

首先引出计算几何学中一个最基本的问题：如何判断向量在的顺时针方向还是逆时针方向？

把p0定为原点，p1的坐标是(x1,y1)，p2的坐标是(x2,y2)。向量的叉积(cross product)实际上就是矩阵的行列式：

当叉积为正时，说明在的顺时针方向上；叉积为0说明两向量共线（同向或反向）。

当同时满足：

（1）和在的两侧（即一个顺时针方向上，一个在逆时针方向上）

（2）和在的两侧

时可肯定和相交。

　　　　　　　　　　　　图1

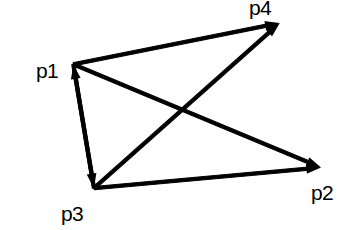
图1是线段相交的一般情形。

图2只满足第（1）条，不满足第（2）条所以不能证明和相交。

　　　　　　　　　　　　图2

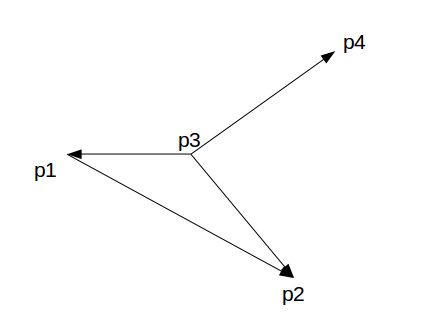
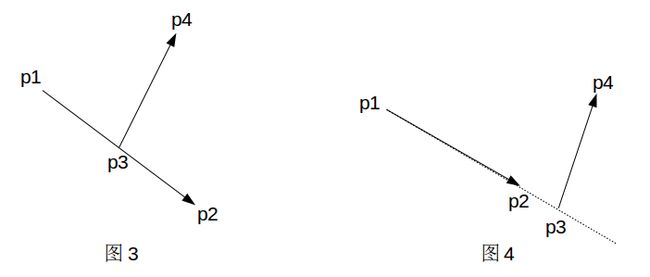
图3和图4是一种特殊情况，它不满足第（2）条，因为和重合,即和的叉积为0。

可见当叉积为0时要分情况讨论，当p3在线段p₁p₂上时两线段相交；当p3在线段p₁p₂的延长线上时两线段不相交。

最后一句话其实也不用分情况讨论，只要改改判断条件就行了，改成d1*d2 <= 0 && d3 * d4 <= 0

#include <cstdio>
#include <iostream>
#include <cmath>
using namespace std;

const double LIMIT = 1e-8;

typedef struct {
	double x, y;
}point, dir;

typedef struct {
	point p1;
	point p2;
}line;

line L[15];

double cross(point pp1, point pp2, point pp3) {
	dir t1, t2;
	t1.x = pp1.x - pp2.x;
	t1.y = pp1.y - pp2.y;
	t2.x = pp3.x - pp2.x;
	t2.y = pp3.y - pp2.y;
	return t1.x * t2.y - t1.y * t2.x;
}

bool IsItersect(line l1, line l2) {
	double d1, d2, d3, d4;
	d1 = cross(l2.p1, l1.p1, l1.p2);
	d2 = cross(l2.p2, l1.p1, l1.p2);
	d3 = cross(l1.p2, l2.p1, l2.p2);
	d4 = cross(l1.p1, l2.p1, l2.p2);
	if ((d1 * d2 < 0 || fabs(d1 * d2) < LIMIT) && (d3 * d4 < 0 || fabs(d3 * d4) < LIMIT)) {  //将d1 * d2 == 0和d3 * d4 == 0的情况包含进来
		return true;
	}
	else {
		return false;
	}
}

int main()
{
	int N;
	while (~scanf("%d", &N) && N) {
		for (int i = 0; i < N; i++)
			scanf("%lf%lf%lf%lf", &L[i].p1.x, &L[i].p1.y, &L[i].p2.x, &L[i].p2.y);
		int cou = 0;
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				if (i != j && IsItersect(L[i], L[j]))
					cou++;
			}
		}
		printf("%d\n", cou / 2);
	}
	return 0;
}