轮廓处理，计算几何和平面划分的函数集合

本文转载，出自：点击打开链接

目录

1 轮廓处理函数
1.1 ApproxChains
1.2 StartReadChainPoints
1.3 ReadChainPoint
1.4 ApproxPoly
1.5 BoundingRect
1.6 ContourArea
1.7 ArcLength
1.8 CreateContourTree
1.9 ContourFromContourTree
1.10 MatchContourTrees
2 计算几何
2.1 MaxRect
2.2 CvBox2D
2.3 PointSeqFromMat
2.4 BoxPoints
2.5 FitEllipse
2.6 FitLine
2.7 ConvexHull2
2.8 CheckContourConvexity
2.9 CvConvexityDefect
2.10 ConvexityDefects
2.11 PointPolygonTest
2.12 MinAreaRect2
2.13 MinEnclosingCircle
2.14 CalcPGH
3 平面划分
3.1 CvSubdiv2D
3.2 CvQuadEdge2D
3.3 CvSubdiv2DPoint
3.4 Subdiv2DGetEdge
3.5 Subdiv2DRotateEdge
3.6 Subdiv2DEdgeOrg
3.7 Subdiv2DEdgeDst
3.8 CreateSubdivDelaunay2D
3.9 SubdivDelaunay2DInsert
3.10 Subdiv2DLocate
3.11 FindNearestPoint2D
3.12 CalcSubdivVoronoi2D
3.13 ClearSubdivVoronoi2D
轮廓处理函数

ApproxChains  用多边形曲线逼近 Freeman 链

CvSeq* cvApproxChains( CvSeq* src_seq, CvMemStorage* storage,
                       int method=CV_CHAIN_APPROX_SIMPLE,
                       double parameter=0, int minimal_perimeter=0, int recursive=0 );
src_seq
涉及其它链的链指针
storage
存储多边形线段位置的缓存
method
逼近方法 (见函数 cvFindContours 的描述).
parameter
方法参数(现在不用).
minimal_perimeter
仅逼近周长大于 minimal_perimeter 轮廓。其它的链从结果中除去。
recursive
如果非 0, 函数从 src_seq 中利用 h_next 和 v_next links 连接逼近所有可访问的链。如果为 0, 则仅逼近单链。这是一个单独的逼近程序。 对同样的逼近标识，函数 cvApproxChains 与 cvFindContours 的工作方式一模一样。它返回发现的第一个轮廓的指针。其它的逼近模块，可以用返回结构中的 v_next 和 v_next 域来访问

StartReadChainPoints   初始化链读取

void cvStartReadChainPoints( CvChain* chain, CvChainPtReader* reader );
chain
链的指针
reader
链的读取状态
函数 cvStartReadChainPoints 初始化一个特殊的读取器 (参考 Dynamic Data Structures 以获得关于集合与序列的更多内容).

ReadChainPoint  得到下一个链的点

CvPoint cvReadChainPoint( CvChainPtReader* reader );
reader
链的读取状态
函数 cvReadChainPoint 返回当前链的点，并且更新读取位置。


ApproxPoly   用指定精度逼近多边形曲线

CvSeq* cvApproxPoly( const void* src_seq, int header_size, CvMemStorage* storage,
                     int method, double parameter, int parameter2=0 );
src_seq
点集数组序列
header_size
逼近曲线的头尺寸
storage
逼近轮廓的容器。如果为 NULL， 则使用输入的序列
method
逼近方法。目前仅支持 CV_POLY_APPROX_DP ， 对应 Douglas-Peucker 算法.
parameter
方法相关参数。对 CV_POLY_APPROX_DP 它是指定的逼近精度
parameter2
如果 src_seq 是序列，它表示要么逼近单个序列，要么在 src_seq 的同一个或低级层次上逼近所有序列 (参考 cvFindContours 中对轮廓继承结构的描述). 如果 src_seq 是点集的数组 (CvMat*) ， 参数指定曲线是闭合 (parameter2!=0) 还是非闭合 (parameter2=0).函数 cvApproxPoly 逼近一个或多个曲线，并返回逼近结果。对多个曲线的逼近，生成的树将与输入的具有同样的结构。(1:1 的对应关系).

BoundingRect   计算点集的最外面（up-right）矩形边界

CvRect cvBoundingRect( CvArr* points, int update=0 );
points
二维点集，点的序列或向量 (CvMat)
update
更新标识。下面是轮廓类型和标识的一些可能组合:
update=0, contour ~ CvContour*: 不计算矩形边界，但直接由轮廓头的 rect 域得到。
update=1, contour ~ CvContour*: 计算矩形边界，而且将结果写入到轮廓头的 rect 域中 header.
update=0, contour ~ CvSeq* or CvMat*: 计算并返回边界矩形
update=1, contour ~ CvSeq* or CvMat*: 产生运行错误 （runtime error is raised）
函数 cvBoundingRect 返回二维点集的最外面 （up-right）矩形边界。

ContourArea   计算整个轮廓或部分轮廓的面积

double cvContourArea( const CvArr* contour, CvSlice slice=CV_WHOLE_SEQ );
contour
轮廓 (边界点的序列或数组).
slice
感兴趣轮廓部分的起始点，缺省是计算整个轮廓的面积。
函数 cvContourArea 计算整个轮廓或部分轮廓的面积。 对后面的情况，面积表示轮廓部分和起始点连线构成的封闭部分的面积。如下图所示：

备注: 轮廓的方向影响面积的符号。因此函数也许会返回负的结果。应用函数 fabs() 得到面积的绝对值。

ArcLength   计算轮廓周长或曲线长度

double cvArcLength( const void* curve, CvSlice slice=CV_WHOLE_SEQ, int is_closed=-1 );
curve
曲线点集序列或数组
slice
曲线的起始点，缺省是计算整个曲线的长度
is_closed
表示曲线是否闭合，有三种情况：
is_closed=0 - 假设曲线不闭合
is_closed>0 - 假设曲线闭合
is_closed<0 - 若曲线是序列，检查 ((CvSeq*)curve)->flags 中的标识 CV_SEQ_FLAG_CLOSED 来确定曲线是否闭合。否则 (曲线由点集的数组 (CvMat*) 表示) 假设曲线不闭合。
函数 cvArcLength 通过依次计算序列点之间的线段长度，并求和来得到曲线的长度。

CreateContourTree   创建轮廓的继承表示形式

CvContourTree* cvCreateContourTree( const CvSeq* contour, CvMemStorage* storage, double threshold );
contour
输入的轮廓
storage
输出树的容器
threshold
逼近精度
函数 cvCreateContourTree 为输入轮廓 contour 创建一个二叉树，并返回树根的指针。如果参数 threshold 小于或等于 0 ,则函数创建一个完整的二叉树。如果 threshold 大于 0 ， 函数用 threshold 指定的精度创建二叉树：如果基线的截断区域顶点小于threshold，该数就停止生长并作为函数的最终结果返回。

ContourFromContourTree   由树恢复轮廓

CvSeq* cvContourFromContourTree( const CvContourTree* tree, CvMemStorage* storage,
                                 CvTermCriteria criteria );
tree
轮廓树
storage
重构的轮廓容器
criteria
停止重构的准则
函数 cvContourFromContourTree 从二叉树恢复轮廓。参数 criteria 决定了重构的精度和使用树的数目及层次。所以它可建立逼近的轮廓。 函数返回重构的轮廓。

MatchContourTrees   用树的形式比较两个轮廓

double cvMatchContourTrees( const CvContourTree* tree1, const CvContourTree* tree2,
                            int method, double threshold );
tree1
第一个轮廓树
tree2
第二个轮廓树
method
相似度。仅支持 CV_CONTOUR_TREES_MATCH_I1 。
threshold
相似度阈值
函数 cvMatchContourTrees 计算两个轮廓树的匹配值。从树根开始通过逐层比较来计算相似度。如果某层的相似度小于 threshold, 则中断比较过程，且返回当前的差值。

计算几何
MaxRect   对两个给定矩形，寻找矩形边界

CvRect cvMaxRect( const CvRect* rect1, const CvRect* rect2 );
rect1
第一个矩形
rect2
第二个矩形
函数 cvMaxRect 寻找包含两个输入矩形的具有最小面积的矩形边界。

CvBox2D   旋转的二维盒子

typedef struct CvBox2D
{
    CvPoint2D32f center;  /* 盒子的中心 */
    CvSize2D32f  size;    /* 盒子的长和宽 */
    float angle;          /* 水平轴与第一个边的夹角，用角度度表示*/
}
CvBox2D;
PointSeqFromMat

从点向量中初始化点序列头部

CvSeq* cvPointSeqFromMat( int seq_kind, const CvArr* mat,
                          CvContour* contour_header,
                          CvSeqBlock* block );
seq_kind
点序列的类型：一系列点(0),曲线(CV_SEQ_KIND_CURVE),封闭曲线(CV_SEQ_KIND_CURVE+CV_SEQ_FLAG_CLOSED) 等等。


mat
输入矩阵。输入应该是连续的一维点向量，类型也应该是CV_32SC2或者CV_32FC2.
contour_header
轮廓头部，被函数初始化。
block
序列块头部，被函数初始化。
函数cvPointSeqFromMat 初始化序列头部，用来创建一个将给定矩阵中的元素形成的"虚拟"序列。没有数据被拷贝。被初始化的头部可以传递给其他任何包含输入点序列的函数。没有额外的元素加入序列，但是一些可能被移除。函数是cvMakeSeqHeaderForArray 的一个特别的变量，然后在内部使用。它返回初始化头部的指针。需要注意的是，包含的边界矩形（CvContour 的rect字段）没有被初始化，如果你需要使用，需要自己调用cvBoundingRect。

以下是使用例子。

CvContour header;
CvSeqBlock block;
CvMat* vector = cvCreateMat( 1, 3, CV_32SC2 );

CV_MAT_ELEM( *vector, CvPoint, 0, 0 ) = cvPoint(100,100);
CV_MAT_ELEM( *vector, CvPoint, 0, 1 ) = cvPoint(100,200);
CV_MAT_ELEM( *vector, CvPoint, 0, 2 ) = cvPoint(200,100);

IplImage* img = cvCreateImage( cvSize(300,300), 8, 3 );
cvZero(img);

cvDrawContours( img, cvPointSeqFromMat(CV_SEQ_KIND_CURVE+CV_SEQ_FLAG_CLOSED,
   vector, &header, &block), CV_RGB(255,0,0), CV_RGB(255,0,0), 0, 3, 8, cvPoint(0,0));
BoxPoints

寻找盒子的顶点
void cvBoxPoints( CvBox2D box, CvPoint2D32f pt[4] );
box
盒子
pt
顶点数组
函数 cvBoxPoints 计算输入的二维盒子的顶点。下面是函数代码：

void cvBoxPoints( CvBox2D box, CvPoint2D32f pt[4] )
{
    double angle = box.angle*CV_PI/180.
    float a = (float)cos(angle)*0.5f;
    float b = (float)sin(angle)*0.5f;

    pt[0].x = box.center.x - a*box.size.height - b*box.size.width;
    pt[0].y = box.center.y + b*box.size.height - a*box.size.width;
    pt[1].x = box.center.x + a*box.size.height - b*box.size.width;
    pt[1].y = box.center.y - b*box.size.height - a*box.size.width;
    pt[2].x = 2*box.center.x - pt[0].x;
    pt[2].y = 2*box.center.y - pt[0].y;
    pt[3].x = 2*box.center.x - pt[1].x;
    pt[3].y = 2*box.center.y - pt[1].y;
}

FitEllipse  二维点集的椭圆拟合

CvBox2D cvFitEllipse2( const CvArr* points );
points
点集的序列或数组
函数 cvFitEllipse 对给定的一组二维点集作椭圆的最佳拟合(最小二乘意义上的)。返回的结构与 cvEllipse 中的意义类似，除了 size 表示椭圆轴的整个长度，而不是一半长度。

FitLine   2D 或 3D 点集的直线拟合

void  cvFitLine( const CvArr* points, int dist_type, double param,
                 double reps, double aeps, float* line );
points
2D 或 3D 点集，32-比特整数或浮点数坐标
dist_type
拟合的距离类型 （见讨论）.
param
对某些距离的数字参数，如果是 0， 则选择某些最优值
reps, aeps
半径 (坐标原点到直线的距离) 和角度的精度，一般设为0.01。
line
输出的直线参数。2D 拟合情况下，它是包含 4 个浮点数的数组 (vx, vy, x0, y0)，其中 (vx, vy) 是线的单位向量而 (x0, y0) 是线上的某个点. 对 3D 拟合，它是包含 6 个浮点数的数组 (vx, vy, vz, x0, y0, z0)， 其中 (vx, vy, vz) 是线的单位向量，而 (x0, y0, z0) 是线上某点。
函数 cvFitLine 通过求 sumi:ρ(ri) 的最小值方法，用 2D 或 3D 点集拟合直线，其中 ri 是第 i 个点到直线的距离， ρ(r) 是下面的距离函数之一：

dist_type=CV_DIST_L2 (L2): ρ(r)=r2/2 (最简单和最快的最小二乘法)

dist_type=CV_DIST_L1 (L1): ρ(r)=r

dist_type=CV_DIST_L12 (L1-L2): ρ(r)=2?[sqrt(1+r2/2) - 1]

dist_type=CV_DIST_FAIR (Fair): ρ(r)=C2?[r/C - log(1 + r/C)], C=1.3998

dist_type=CV_DIST_WELSCH (Welsch): ρ(r)=C2/2?[1 - exp(-(r/C)2)], C=2.9846

dist_type=CV_DIST_HUBER (Huber): ρ(r)= r2/2, if r < C; C?(r-C/2), otherwise; C=1.345

ConvexHull2   发现点集的凸外形

CvSeq* cvConvexHull2( const CvArr* input, void* hull_storage=NULL,
                      int orientation=CV_CLOCKWISE, int return_points=0 );
points
2D 点集的序列或数组，32-比特整数或浮点数坐标
hull_storage
输出的数组(CvMat*) 或内存缓存 (CvMemStorage*)，用以存储凸外形。 如果是数组，则它应该是一维的，而且与输入的数组/序列具有同样数目的元素。输出时，通过修改头结构将数组裁减到凸外形的尺寸。
orientation
凸外形的旋转方向: 逆时针或顺时针 （CV_CLOCKWISE or CV_COUNTER_CLOCKWISE）
return_points
如果非零，hull_storage 为数组情况下,点集将以外形 (hull) 存储，而不是顶点形式 (indices)。如果 hull_storag 为内存存储模式下则存储为点集形式(points)。
函数 cvConvexHull2 使用 Sklansky 算法计算 2D 点集的凸外形。如果 hull_storage 是内存存储仓， 函数根据 return_points 的值，创建一个包含外形的点集或指向这些点的指针的序列。

例子. 由点集序列或数组创建凸外形
#include "cv.h"
#include "highgui.h"
#include <stdlib.h>
#define ARRAY  0 /* switch between array/sequence method by replacing 0<=>1 */

void main( int argc, char** argv )
{
    IplImage* img = cvCreateImage( cvSize( 500, 500 ), 8, 3 );
    cvNamedWindow( "hull", 1 );

#if !ARRAY
        CvMemStorage* storage = cvCreateMemStorage();
#endif
    for(;;)
    {
        int i, count = rand()%100 + 1, hullcount;
        CvPoint pt0;
#if !ARRAY
        CvSeq* ptseq = cvCreateSeq( CV_SEQ_KIND_GENERIC|CV_32SC2, sizeof(CvContour),
                                     sizeof(CvPoint), storage );
        CvSeq* hull;

        for( i = 0; i < count; i++ )
        {
            pt0.x = rand() % (img->width/2) + img->width/4;
            pt0.y = rand() % (img->height/2) + img->height/4;
            cvSeqPush( ptseq, &pt0 );
        }
        hull = cvConvexHull2( ptseq, 0, CV_CLOCKWISE, 0 );
        hullcount = hull->total;
#else
        CvPoint* points = (CvPoint*)malloc( count * sizeof(points[0]));
        int* hull = (int*)malloc( count * sizeof(hull[0]));
        CvMat point_mat = cvMat( 1, count, CV_32SC2, points );
        CvMat hull_mat = cvMat( 1, count, CV_32SC1, hull );

        for( i = 0; i < count; i++ )
        {
            pt0.x = rand() % (img->width/2) + img->width/4;
            pt0.y = rand() % (img->height/2) + img->height/4;
            points[i] = pt0;
        }
        cvConvexHull2( &point_mat, &hull_mat, CV_CLOCKWISE, 0 );
        hullcount = hull_mat.cols;
#endif
        cvZero( img );
        for( i = 0; i < count; i++ )
        {
#if !ARRAY
            pt0 = *CV_GET_SEQ_ELEM( CvPoint, ptseq, i );
#else
            pt0 = points[i];
#endif
            cvCircle( img, pt0, 2, CV_RGB( 255, 0, 0 ), CV_FILLED );
        }

#if !ARRAY
        pt0 = **CV_GET_SEQ_ELEM( CvPoint*, hull, hullcount - 1 );
#else
        pt0 = points[hull[hullcount-1]];
#endif
        for( i = 0; i < hullcount; i++ )
        {
#if !ARRAY
            CvPoint pt = **CV_GET_SEQ_ELEM( CvPoint*, hull, i );
#else
            CvPoint pt = points[hull[i]];
#endif
            cvLine( img, pt0, pt, CV_RGB( 0, 255, 0 ));
            pt0 = pt;
        }
        cvShowImage( "hull", img );
        int key = cvWaitKey(0);
        if( key == 27 ) // 'ESC'
            break;
#if !ARRAY
        cvClearMemStorage( storage );
#else
        free( points );
        free( hull );
#endif
    }
}
CheckContourConvexity

测试轮廓的凸性
int cvCheckContourConvexity( const CvArr* contour );
contour
被测试轮廓 (点序列或数组).
函数 cvCheckContourConvexity 输入的轮廓是否为凸的。必须是简单轮廓，比如没有自交叉。
CvConvexityDefect

用来描述一个简单轮廓凸性缺陷的结构体
typedef struct CvConvexityDefect
{
    CvPoint* start; /* 缺陷开始的轮廓点 */
    CvPoint* end; /* 缺陷结束的轮廓点 */
    CvPoint* depth_point; /* 缺陷中距离凸形最远的轮廓点(谷底) */
    float depth; /* 谷底距离凸形的深度*/
} CvConvexityDefect;
Picture. 手部轮廓的凸形缺陷.

发现轮廓凸形缺陷
CvSeq* cvConvexityDefects( const CvArr* contour, const CvArr* convexhull,
                           CvMemStorage* storage=NULL );
contour
输入轮廓
convexhull
用 cvConvexHull2 得到的凸外形，它应该包含轮廓的定点的指针或下标，而不是外形点的本身，即cvConvexHull2 中的参数 return_points 应该设置为 0.
storage
凸性缺陷的输出序列容器。如果为 NULL, 使用轮廓或外形的存储仓。
函数 cvConvexityDefects 发现输入轮廓的所有凸性缺陷，并且返回 CvConvexityDefect 结构序列。

PointPolygonTest测试点是否在多边形中
double cvPointPolygonTest( const CvArr* contour,
                           CvPoint2D32f pt, int measure_dist );
contour
输入轮廓.
pt
针对轮廓需要测试的点。
measure_dist
如果非0，函数将估算点到轮廓最近边的距离。
函数cvPointPolygonTest 决定测试点是否在轮廓内，轮廓外，还是轮廓的边上（或者共边的交点上），它的返回值是正负零，相对应的，当measure_dist=0时，返回值是1, -1,0, 同样当 measure_dist≠0 ，它是返回一个从点到最近的边的带符号距离。

下面是函数输出的结果，用图片的每一个象素去测试轮廓的结果。

ConvexityDefects
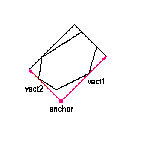
MinAreaRect2  对给定的 2D 点集，寻找最小面积的包围矩形

CvBox2D  cvMinAreaRect2( const CvArr* points, CvMemStorage* storage=NULL );
points
点序列或点集数组
storage
可选的临时存储仓
函数 cvMinAreaRect2 通过建立凸外形并且旋转外形以寻找给定 2D 点集的最小面积的包围矩形.

Picture. Minimal-area bounding rectangle for contour

MinEnclosingCircle  对给定的 2D 点集，寻找最小面积的包围圆形

int cvMinEnclosingCircle( const CvArr* points, CvPoint2D32f* center, float* radius );
points
点序列或点集数组
center
输出参数：圆心
radius
输出参数：半径
函数 cvMinEnclosingCircle 对给定的 2D 点集迭代寻找最小面积的包围圆形。如果产生的圆包含所有点，返回非零。否则返回零（算法失败）。

CalcPGH  计算轮廓的 pair-wise 几何直方图

void cvCalcPGH( const CvSeq* contour, CvHistogram* hist );
contour
输入轮廓，当前仅仅支持具有整数坐标的点集
hist
计算出的直方图，必须是两维的。
函数 cvCalcPGH 计算轮廓的 2D pair-wise 几何直方图 （2D pair-wise geometrical histogram ：PGH), 算法描述见 [Iivarinen97]. 算法考虑的每一对轮廓边缘。计算每一对边缘之间的夹角以及最大最小距离。具体做法是，轮流考虑每一个边缘做为基准，函数循环遍历所有其他的边缘。在考虑基准边缘和其它边缘的时候， 选择非基准线上的点到基准线上的最大和最小距离。边缘之间的角度定义了直方图的行，而在其中增加对应计算出来的最大和最小距离的所有直方块， (即直方图是 [Iivarninen97] 定义中的转置). 该直方图用来做轮廓匹配。

平面划分

CvSubdiv2D  平面划分

#define CV_SUBDIV2D_FIELDS()        CV_GRAPH_FIELDS()               int  quad_edges;                int  is_geometry_valid;         CvSubdiv2DEdge recent_edge;     CvPoint2D32f  topleft;          CvPoint2D32f  bottomright;

typedef struct CvSubdiv2D
{
    CV_SUBDIV2D_FIELDS()
}
CvSubdiv2D;
平面划分是将一个平面分割为一组互不重叠的能够复盖整个平面的区域P(facets)。上面结构描述了建立在 2D 点集上的划分结构，其中点集互相连接并且构成平面图形，该图形通过结合一些无限连接外部划分点(称为凸形点)的边缘，将一个平面用边按照其边缘划分成很多小区域(facets)。

对于每一个划分操作，都有一个对偶划分与之对应，对偶的意思是小区域和点(划分的顶点)变换角色，即在对偶划分中，小区域被当做一个顶点(以下称之为虚拟点)，而原始的划分顶点被当做小区域。在如下所示的图例中，原始的划分用实线来表示，而对偶划分用点线来表示。

OpenCV 使用Delaunay's 算法将平面分割成小的三角形区域。分割的实现通过从一个假定的三角形(该三角形确保包括所有的分割点)开始不断迭代来完成。在这种情况下，对偶划分就是输入的2d点集的 Voronoi图表。这种划分可以用于对一个平面的3d分段变换、形态变换、平面点的快速定位以及建立特定的图结构 (比如 NNG,RNG等等)。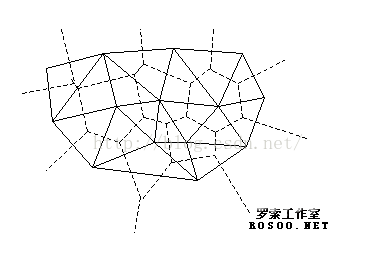

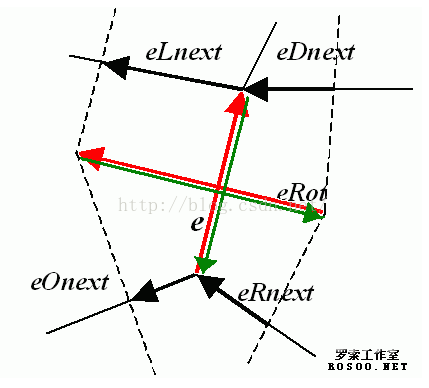
CvQuadEdge2D  平面划分中的Quad-edge(四方边缘结构)

/* quad-edge中的一条边缘，低两位表示该边缘的索引号，其它高位表示边缘指针。 */
typedef long CvSubdiv2DEdge;

/* 四方边缘的结构场 */
#define CV_QUADEDGE2D_FIELDS()         int flags;                         struct CvSubdiv2DPoint* pt[4];     CvSubdiv2DEdge  next[4];

typedef struct CvQuadEdge2D
{
    CV_QUADEDGE2D_FIELDS()
}
CvQuadEdge2D;
Quad-edge(译者注：以下称之为四方边缘结构)是平面划分的基元，其中包括四个边缘 (e, eRot(红色) 以及它们的逆（绿色）)。

CvSubdiv2DPoint  原始和对偶划分点

#define CV_SUBDIV2D_POINT_FIELDS()    int            flags;          CvSubdiv2DEdge first;          CvPoint2D32f   pt;

#define CV_SUBDIV2D_VIRTUAL_POINT_FLAG (1 << 30)

typedef struct CvSubdiv2DPoint
{
    CV_SUBDIV2D_POINT_FIELDS()
}
CvSubdiv2DPoint;

Subdiv2DGetEdge  返回给定的边缘之一

CvSubdiv2DEdge  cvSubdiv2DGetEdge( CvSubdiv2DEdge edge, CvNextEdgeType type );
#define cvSubdiv2DNextEdge( edge ) cvSubdiv2DGetEdge( edge, CV_NEXT_AROUND_ORG )
edge
划分的边缘 (并不是四方边缘结构)
type
确定函数返回哪条相关边缘，是下面几种之一：
CV_NEXT_AROUND_ORG - 边缘原点的下一条 (eOnext on the picture above if e is the input edge)
CV_NEXT_AROUND_DST - 边缘顶点的下一条 (eDnext)
CV_PREV_AROUND_ORG - 边缘原点的前一条 (reversed eRnext)
CV_PREV_AROUND_DST - 边缘终点的前一条 (reversed eLnext)
CV_NEXT_AROUND_LEFT - 左区域的下一条 (eLnext)
CV_NEXT_AROUND_RIGHT - 右区域的下一条(eRnext)
CV_PREV_AROUND_LEFT - 左区域的前一条 (reversed eOnext)
CV_PREV_AROUND_RIGHT - 右区域的前一条 (reversed eDnext)
函数 cvSubdiv2DGetEdge 返回与输入边缘相关的边缘

Subdiv2DRotateEdge  返回同一个四方边缘结构中的另一条边缘

CvSubdiv2DEdge  cvSubdiv2DRotateEdge( CvSubdiv2DEdge edge, int rotate );
edge
划分的边缘 (并不是四方边缘结构)
type
确定函数根据输入的边缘返回同一四方边缘结构中的哪条边缘，是下面几种之一:
0 - 输入边缘 (上图中的e，如果e是输入边缘)
1 - 旋转边缘 (eRot)
2 -逆边缘 ( e的反向边缘)
3 - 旋转边缘的反向边缘(eRot的反向边缘， 图中绿色)
函数 cvSubdiv2DRotateEdge 根据输入的边缘返回四方边缘结构中的一条边缘

Subdiv2DEdgeOrg 返回边缘的原点

CvSubdiv2DPoint* cvSubdiv2DEdgeOrg( CvSubdiv2DEdge edge );
edge
划分的边缘 (并不是四方边缘结构)
函数 cvSubdiv2DEdgeOrg 返回边缘的原点。如果该边缘是从对偶划分得到并且虚点坐标还没有计算出来，可能返回空指针。虚点可以用函数来cvCalcSubdivVoronoi2D计算。

Subdiv2DEdgeDst

Returns edge destination

CvSubdiv2DPoint* cvSubdiv2DEdgeDst( CvSubdiv2DEdge edge );
edge
划分的边缘 (并不是四方边缘结构)
函数 cvSubdiv2DEdgeDst 返回边缘的终点。如果该边缘是从对偶划分得到并且虚点坐标还没有计算出来，可能返回空指针。虚点可以用函数来cvCalcSubdivVoronoi2D计算。

CreateSubdivDelaunay2D 生成的空Delaunay 三角测量

CvSubdiv2D* cvCreateSubdivDelaunay2D( CvRect rect, CvMemStorage* storage );
rect
Rectangle包括所有待加入划分操作的2d点的四方形。
storage
划分操作的存储器
函数 cvCreateSubdivDelaunay2D 生成一个空的Delaunay 划分, 其中2d points可以进一步使用函数 cvSubdivDelaunay2DInsert来添加。所有的点一定要在指定的四方形中添加，否则就会报运行错误。

SubdivDelaunay2DInsert  向 Delaunay三角测量中插入一个点

CvSubdiv2DPoint*  cvSubdivDelaunay2DInsert( CvSubdiv2D* subdiv, CvPoint2D32f pt);
subdiv
通过函数 cvCreateSubdivDelaunay2D.生成的Delaunay划分
pt
待插入的点
函数 cvSubdivDelaunay2DInsert 向划分的结构中插入一个点并且正确地改变划分的拓朴结构。如果划分结构中已经存在一个相同的坐标点，则不会有新点插入。该函数返回指向已插入点的指针。在这个截断，不计算任何虚点坐标。

Subdiv2DLocate 在 Delaunay三角测量中定位输入点

CvSubdiv2DPointLocation  cvSubdiv2DLocate( CvSubdiv2D* subdiv, CvPoint2D32f pt,
                                           CvSubdiv2DEdge* edge,
                                           CvSubdiv2DPoint** vertex=NULL );
subdiv
Delaunay 或者是其它分割结构.
pt
待定位的输入点
edge
与输入点对应的输入边缘(点在其上或者其右)
vertex
与输入点对应的输出顶点坐标(指向double类型)，可选。
函数 cvSubdiv2DLocate 在划分中定位输入点，共有5种类型:

输入点落入某小区域内。 函数返回参数　CV_PTLOC_INSIDE 且*edge 中包含小区域的边缘之一。
输入点落p在边缘之上。 函数返回参数 CV_PTLOC_ON_EDGE 且 *edge 包含此边缘。
输入点与划分的顶点之一相对应。 函数返回参数 CV_PTLOC_VERTEX 且 *vertex 中包括指向该顶点的指针；
输入点落在划分的参考区域之外。 函数返回参数 CV_PTLOC_OUTSIDE_RECT且不填写任何指针。
输入参数之一有误。函数报运行错误(如果已经选则了沉默或者父母出错模式，则函数返回CV_PTLOC_ERROR) 。

FindNearestPoint2D 根据输入点，找到其最近的划分顶点

CvSubdiv2DPoint* cvFindNearestPoint2D( CvSubdiv2D* subdiv, CvPoint2D32f pt );
subdiv
Delaunay或者其它划分方式
pt
输入点
函数 cvFindNearestPoint2D 是另一个定位输入点的函数。该函数找到输入点的最近划分顶点。尽管划分出的小区域(facet)被用来作为起始点，但是输入点不一定非得在最终找到的顶点所在的小区域之内。该函数返回指向找到的划分顶点的指针。

CalcSubdivVoronoi2D  计算Voronoi图表的细胞结构

void cvCalcSubdivVoronoi2D( CvSubdiv2D* subdiv );
subdiv
Delaunay 划分,其中所有的点已经添加 。
函数 cvCalcSubdivVoronoi2D 计算虚点的坐标，所有与原划分中的某顶点相对应的虚点形成了(当他们相互连接时)该顶点的Voronoi 细胞的边界。

ClearSubdivVoronoi2D  移除所有的虚点

void cvClearSubdivVoronoi2D( CvSubdiv2D* subdiv );
subdiv
Delaunay 划分
函数 cvClearSubdivVoronoi2D 移除所有的虚点。当划分的结果被函数cvCalcSubdivVoronoi2D的前一次调用更改时，该函数被cvCalcSubdivVoronoi2D内部调用 。

（完）