回归分析作业3

作业内容：

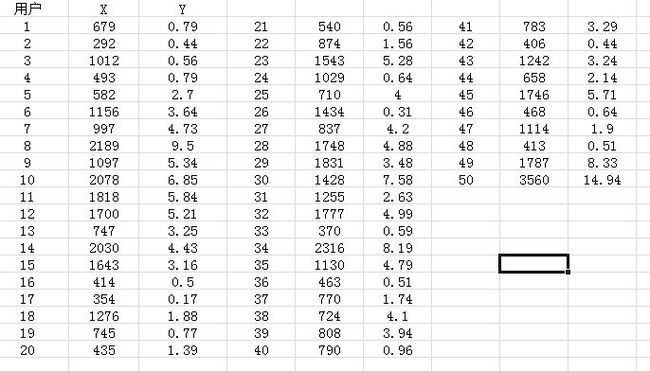
研究用电高峰时居民家庭每小时的用电量Y 与每月总用电量X之间的关系。53户居民某

月用电记录见\3-15.xlsx"，试完成以下统计分析：
(1) 应用最小二乘法求经验回归方程；
(2) 以拟合值^yi为横坐标，学生化残差ri为纵坐标，作残差图，分析Gauss-Markov假设对
本例的适用性；
(3) 考虑因变量的变换U = sqrt(Y)，再对新变量U和X重复(1)和(2)的统计分析；
(4) 将Box-Cox变换应用到本例，计算变换参数¸的值，并做讨论；

(5) 做影响分析，找出强影响点。

数据内容：

我的答案（仅供参考）

1、

A<-read.csv("3-15.csv")
lm.reg<-lm(Y~X,data=A)
#Coefficients:
#(Intercept)            X  
#  -0.788008     0.003619 

2、

y.stu<-rstudent(lm.reg)
y.fit<-predict(lm.reg)
plot(y.stu~y.fit)
#主差齐性不成立
par(mfrow=c(2,2))
plot(lm.reg)

                                                                

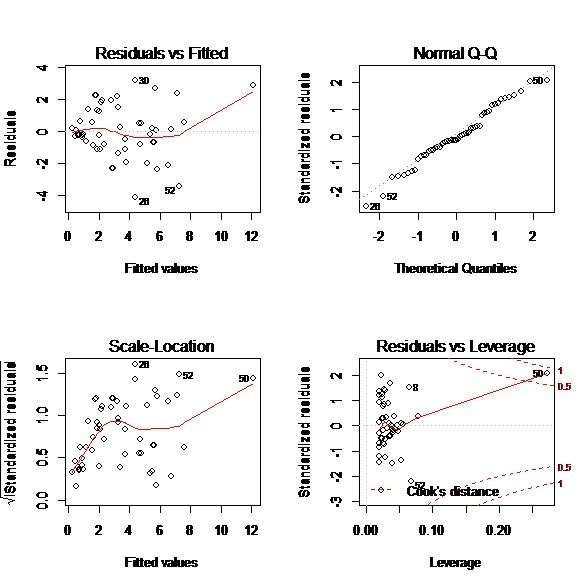
3、

lm.new<-update(lm.reg,sqrt(.)~.)
summary(lm.new)
#Coefficients:
#(Intercept)            X  
#  0.5895689    0.0009396 
par(mfrow=c(1,1))
y.stu<-rstudent(lm.new)
y.fit<-predict(lm.new)
plot(y.stu~y.fit)
par(mfrow=c(2,2))
plot(lm.new)

                                                        

结论：在作了开方变换后，残差表现为在y=0附近波动，具有齐方差性。我们也可以进一步猜想：使用box-cox变换lambda的取值也该在0.5附近

4、

library(MASS)
par(mfrow=c(1,1))
boxcox(lm.reg,lambda = seq(-1, 1, length = 50))
which.max(box$y)
#77
box$x[77]
#0.5353535

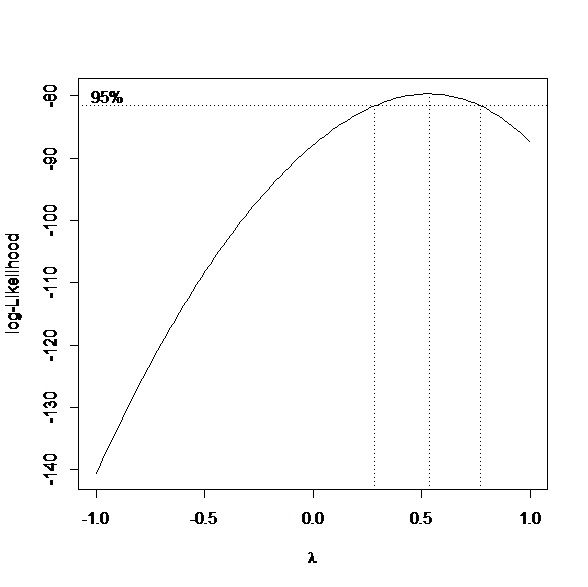
这里可以看到lambda的取值约为0.535，为了使得变换好解释，可调整为lambda=0.5

5、

cook<-cooks.distance(lm.reg)
cook[cook>4/53]
#         8         50         52 
#0.08098912 0.80377856 0.17563786

用cook距离得到强影响点应该为8,50,52

可以看看去掉一组数据后的回归系数来感受异常点带来的影响：

lm.influence(lm.reg)

部分输出结果：

$coefficients
     (Intercept)             X
1  -0.0393853151  1.920996e-05
2   0.0114405833 -6.915937e-06
3  -0.0625231265  1.548502e-05
4  -0.0113553157  6.299241e-06
5   0.0692992606 -3.644878e-05
6   0.0047731233 -5.493597e-08
7   0.0531184053 -1.407280e-05
8  -0.0852683125  1.145997e-04
9   0.0487118877 -6.198858e-06
10 -0.0035146664  5.067403e-06
11 -0.0007546488  1.483751e-06
12  0.0013770422 -3.764625e-06
13  0.0548807287 -2.498762e-05
14  0.0573408813 -8.586983e-05
15  0.0118615907 -4.364976e-05
16 -0.0125293336  7.222393e-06
17 -0.0203839572  1.204634e-05
18 -0.0258254894 -1.006395e-05
19 -0.0469030468  2.140383e-05
20  0.0352863810 -2.014768e-05
21 -0.0318094556  1.718305e-05
22 -0.0279490278  1.052911e-05
23 -0.0003255986  8.358252e-06
24 -0.0599760416  1.360578e-05
25  0.0956672991 -4.531033e-05
26 -0.0205658103 -5.027818e-05
27  0.0710783963 -2.861559e-05
28  0.0075753364 -1.758391e-05
29  0.0377033247 -7.233015e-05
30  0.0170906336  3.846450e-05
31 -0.0161089291 -4.739595e-06
32  0.0085313955 -1.833973e-05
33  0.0024324183 -1.428421e-06
34 -0.0260055242  3.292257e-05
35  0.0310397481 -2.071044e-06
36 -0.0214490818  1.208351e-05
37 -0.0102999208  4.563105e-06
38  0.0960712852 -4.485485e-05
39  0.0682516943 -2.873485e-05
40 -0.0430904920  1.860305e-05
41  0.0487545927 -2.124459e-05
42 -0.0144921536  8.383218e-06
43 -0.0070021436 -1.695181e-06
44  0.0251347390 -1.248541e-05
45 -0.0020539756  4.795485e-06
46 -0.0150137050  8.437032e-06
47 -0.0291206624  2.832585e-06
48 -0.0117284902  6.763746e-06
49 -0.0361061581  7.580521e-05
50 -0.4056284728  4.129234e-04
51  0.0008991617  7.352304e-06
52  0.1288033831 -1.702306e-04
53 -0.0001762253 -1.324578e-05