最短路劲

HDU-2544-最短路

http://acm.hdu.edu.cn/showproblem.php?pid=2544

 赤裸裸的Dijkstra

Dijkstra算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define maxvalue 0x7fffffff
int map[105][105];
int n,m;
int dijkstra()
{
	int i,j,v,temp;
	int dis[105];
	int visit[105];
	for(i=1;i<=n;i++)
	dis[i]=map[1][i];
	dis[1]=0;
	memset(visit,0,sizeof(visit));
	visit[1]=1;
	for(i=1;i<n;i++)
	{
		temp=maxvalue;
		v=1;
		for(j=1;j<=n;j++)
		if(visit[j]==0&&dis[j]<temp)
		{
			v=j;
			temp=dis[j];
		}
		visit[v]=1;
		for(j=1;j<=n;j++)
		if(visit[j]==0&&map[v][j]<maxvalue&&dis[j]>dis[v]+map[v][j])  //少了map[v][j]<maxvalue会WA
		dis[j]=dis[v]+map[v][j];
	}
	return dis[n];
}
int main()
{
	int i,j,ans;
	int a,b,c;
	while(scanf("%d %d",&n,&m),n||m)
	{
		for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)
		map[i][j]=maxvalue;
		while(m--)
		{
			scanf("%d %d %d",&a,&b,&c);
			if(map[a][b]>c)   //防止有重边
			{
				map[a][b]=map[b][a]=c;
			}
		}
		ans=dijkstra();
		printf("%d\n",ans);
	}
	return 0;
}

这题用floyd也能做

Floyd是通过一个图的邻接矩阵求出它的每两点间的最短路径矩阵，时间复杂度为O(n^3)

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define maxvalue 0x7fffffff
int map[105][105];
int n,m;
int floyd()
{
	int i,j,k;
	for(k=1;k<=n;k++)
	for(i=1;i<=n;i++)
	for(j=1;j<=n;j++)
	{
		if(map[i][k]<maxvalue&&map[k][j]<maxvalue&&map[i][k]+map[k][j]<map[i][j])
		map[i][j]=map[i][k]+map[k][j];
	}
	return map[1][n];
}
int main()
{
	int i,j,ans;
	int a,b,c;
	while(scanf("%d %d",&n,&m),n||m)
	{
		for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)
		map[i][j]=maxvalue;
		while(m--)
		{
			scanf("%d %d %d",&a,&b,&c);
			if(map[a][b]>c)   //防止有重边
			{
				map[a][b]=map[b][a]=c;
			}
		}
		ans=floyd();
		printf("%d\n",ans);
	}
	return 0;
}

用dijkstra和floyd也可以求出最短路劲的序列，即从始点至终点要依次经过哪些点

比如说求如下图，从V1至V10的最短路劲序列

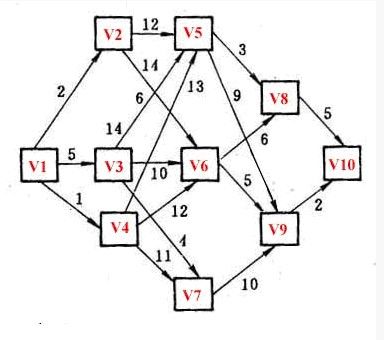
输入邻接矩阵，-1表示两点之间没有路劲

dijkstra

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define maxint 0x7fffffff
int map[15][15];
int dis[15];
int visit[15];
int prev[15];
void print(int x)
{
    int k;
	k=prev[x];
	if(k==1)
	return;
	print(k);
	printf(" %d",k);
}
void dijkstra()
{
	int i,j,v,min;
	memset(visit,0,sizeof(visit));
	visit[1]=1;
	for(i=1;i<=10;i++)
	{
        dis[i]=map[1][i];
		if(dis[i]==maxint)
		prev[i]=0;
		else
		prev[i]=1;
	}
	for(i=1;i<10;i++)
	{
		min=maxint;
		for(j=1;j<=10;j++)
        {
			if(!visit[j]&&dis[j]<min)
			{
				min=dis[j];
				v=j;
			}
		}
		visit[v]=1;
		for(j=1;j<=10;j++)
		if(!visit[j]&&map[v][j]!=maxint&&dis[j]>map[v][j]+dis[v])
        {
			dis[j]=map[v][j]+dis[v];
			prev[j]=v;
		}
	}
}
int main()
{
	int i,j;
	for(i=1;i<=10;i++)
	for(j=1;j<=10;j++)
	{
		scanf("%d",&map[i][j]);
		if(map[i][j]==-1)
		map[i][j]=maxint;
	}
	dijkstra();
	printf("1");
	print(10);
	printf(" 10\n");
    return 0;
}

floyd

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
int dis[15][15];
int path[15][15];
void floyd()
{
	int i,j,k;
	memset(path,0,sizeof(path));
	for(k=1;k<=10;k++)
	for(i=1;i<=10;i++)
	for(j=1;j<=10;j++)
	if(dis[i][k]!=-1&&dis[k][j]!=-1&&(dis[i][j]==-1||dis[i][j]>dis[i][k]+dis[k][j]))
	{
		dis[i][j]=dis[i][k]+dis[k][j];
		path[i][j]=k;
	}
}
void print(int i,int j)
{
    int k;
	k=path[i][j];
	if(k==0)
	return;
	print(i,k);
	printf(" %d",k);
	print(k,j);
}
int main()
{
	int i,j;
	for(i=1;i<=10;i++)
	for(j=1;j<=10;j++)
	scanf("%d",&dis[i][j]);
	floyd();
	printf("1");
	print(1,10);
	printf(" 10\n");
	return 0;
}

结果均为1 3 5 8 10

POJ-3268-Silver Cow Party

http://poj.org/problem?id=3268

很有意思的一题，题意是： n头牛要去参加一场在编号为x的牛的农场举行的派对,每头牛都必须参加完派对后回到家，每头牛都会选择最短路径，求这n个牛的最短路径（一个来回）中最长的一条的长度。

dijkstra用于计算一个节点到其他所有节点的最短路径，将邻接矩阵转置，可求得其他所有节点到该节点的最短路劲

先求出x点到各点的最短路径放到数组dis1中，再将邻接矩阵转置，求出各点到x点的最短路径放到数组dis2中，求出max(dis1 + dis2)即可

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define max 0x7fffff
int map[1005][1005];
int dis1[1005];
int dis2[1005];
int n,m,x;
void dijkstra(int dis[])
{
	int i,j,v,min;
	int visit[1005];
	memset(visit,0,sizeof(visit));
	for(i=1;i<=n;i++)
	dis[i]=map[x][i];
	dis[x]=0;
	visit[x]=1;
	for(i=1;i<=n;i++)
	{
		min=max;
		for(j=1;j<=n;j++)
		{
			if(!visit[j]&&dis[j]<min)
			{
				min=dis[j];
				v=j;
			}
		}
		visit[v]=1;
		for(j=1;j<=n;j++)
	    if(!visit[j]&&dis[v]+map[v][j]<dis[j])
		dis[j]=dis[v]+map[v][j];
	}
}
void tran()
{
	int i,j,temp;
	for(i=1;i<=n;i++)
	for(j=1;j<=i;j++)
	{
		temp=map[i][j];
		map[i][j]=map[j][i];
		map[j][i]=temp;
	}
}
int main()
{
	int a,b,c,i,j;
	int ans;
	while(scanf("%d%d%d",&n,&m,&x)!=EOF)
	{
		for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)
		map[i][j]=max;
		while(m--)
		{
			scanf("%d%d%d",&a,&b,&c);
			if(map[a][b]>c)
			map[a][b]=c;
		}
		dijkstra(dis1);  //x点到各点的最短路径
		tran();
		dijkstra(dis2);  //各点到x点的最短路径
		ans=-1;
		for(i=1;i<=n;i++)
		{
			if(i!=x&&dis1[i]+dis2[i]>ans)
			ans=dis1[i]+dis2[i];
		}
		printf("%d\n",ans);
	}
	return 0;
}