UFLDL学习笔记2(Preprocessing: PCA and Whitening)
最近在学习UFLDL Tutorial,这是一套关于无监督学习的教程。在此感觉Andrew Ng做的真的是非常认真。下面把我的代码贴出来,方便大家学习调试。所有代码已经过matlab调试通过。
PCA是一种用来降维的方法。个人推荐看Pattern Recognition And Machine Learning的第十二章作为辅助。该书写的极为详细。UFLDL上有两个练习。建议先做pca_2d.m,然后的pca_gen.m只需要把代码稍稍改动就可以了。这两个练习都只需要修改一个.m文件,相比上一节稀疏编码要容易一些。以下贴出了我自己的代码和运行结果。
一、pca_2d.m中的代码
Step 1a,获得正交变换的基,代码:
[dim,sampleN] = size(x); %维数与样本数 x = x - mean(x,2)*ones(1,sampleN); %使每维均值为0,这个与UFLDL上给的稍有出入。我认为我是对的。UFLDL上针对图片处理也有一定道理稍后讲 S = x*x' / sampleN; %协方差矩阵 [U,D] = eig(S); %u为列特征向量,D为特征值对角阵 U = fliplr(U); %按照特征值由大到小排列 D = fliplr(fliplr(D)'); %同上Step 1b,获得变换后的坐标。代码:
xRot = U'*x; %经过正交变换后的坐标Step 2,约简到1维。代码:
U_reduce = zeros(dim); %初始化 U_reduce(:,1) = U(:,1); %只选第一个特征向量 y = U_reduce'*x; %变换域的坐标 xHat = U_reduce * y; %反变换回来Step 3,PCA Whitening。目的:(1)去相关 (2)使方差一致。代码:
eig_value = diag(D); %特征值 normalize = sqrt(eig_value+epsilon); %白化系数 xPCAWhite = U'*x ./ (normalize*ones(1,sampleN)); %白化Step3,ZCA Whitening。目的:使白化后数据接近原始数据。代码:
xZCAWhite = U * xPCAWhite;
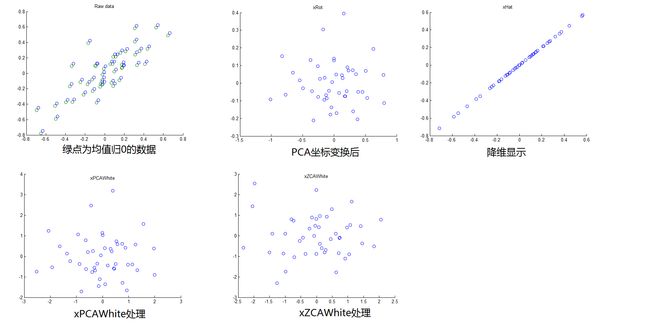
运行结果:
我的结果与UFLDL上给出的答案稍有不同。但基本思想应该是正确的。二、pca_gen.m
Step 0b,数据均值归0化。代码:
[dim,sampleN] = size(x); %维数与样本数 x = x - repmat(mean(x,2),1,sampleN);%标准PCA均值归0 x = x - repmat(mean(x,1),dim,1); %使每维均值为0,理论上标准的PCA应用上式,但由处理图像的物理意义该用此式这里要注意一下第三行。理论上应该使用第二行做均值归0,但是图像每个像素点之间是很相关的。通常图像中的做法是将一幅图片做归0处理,而不是对所有图片的某个像素点做归0。这样做不会有太大影响。这一点我想了好久,也是我个人的理解。结果显示在Fig2中。
Step 1a,获得正交变换的基,代码:
S = x*x' / sampleN; %协方差矩阵 [U,D] = eig(S); %特征向量与特征值 U = fliplr(U); %U为列特征向量,D为特征值对角阵 D = fliplr(fliplr(D)'); %按照特征值由大到小排列 y = U'*x; %同上Step 1b,检查变换后的结果。变换后的数据应该是不相关的,因此协方差矩阵应为对角线。代码:
covar = y*y'; %获得变换后数据的协方差矩阵
结果如Fig3。
Step 2,获得前k个主分量。这k个值包含90%的能量。代码:
var_total = sum(D(:)) %总方差
var_cur = 0; %方差计数
for k = 1:dim
var_cur = var_cur + D(k,k); %累计
if (var_cur / var_total) > 0.90 %如果能量已>90%,则跳出for语句
break;
end
end
Step 3,降维数据并显示恢复结果。代码:
U_reduce = zeros(dim); %初始化 U_reduce(:, 1:k) = U(:, 1:k); %去掉特征值小的特征向量(降维) y = U_reduce'*x; %变换 xHat = U_reduce*y; %反变换回来假如保存前90%的能量,PCA可以用44个特征代表144个特征。 Fig3为用44个特征恢复后的数据。Fig4为原始数据。
Step 4a,白化及包含正则的PCA。目的:使得特征的方差取值范围基本一致。代码:
eig_value = diag(D); %特征值 normalize = sqrt(eig_value+epsilon); %白化系数 xPCAWhite = U'*x ./ (normalize*ones(1,sampleN));%白化Step 4b,检查上一步中的结果。如果epsilon为0,则结果应为全1对角阵。如果epsilon为一较小的数,结果应为近似全1的对角阵。代码:
covar = xPCAWhite*xPCAWhite' / sampleN; %协方差矩阵如Fig5所示。
Step 5,ZCA Whitening。白化后使数据最接近原始数据。代码:
xZCAWhite = U * xPCAWhite; %ZCA白化Fig6为ZCA白化后的结果,Fig7为原始图像。可以发现ZCA白化更明显地提取了图像边缘。
运行结果:
上一节稀疏编码调了好几天,有了一些经验,这一节总体上是不难的,细心一些就会得出结果。