卡尔曼滤波器跟踪

1． 什么是卡尔曼滤波器
（What is the Kalman Filter?）

在学习卡尔曼滤波器之前，首先看看为什么叫“卡尔曼”。跟其他著名的理论（例如傅立叶变换，泰勒级数等等）一样，卡尔曼也是一个人的名字，而跟他们不同的是，他是个现代人！

卡尔曼全名Rudolf Emil Kalman，匈牙利数学家，1930年出生于匈牙利首都布达佩斯。1953，1954年于麻省理工学院分别获得电机工程学士及硕士学位。1957年于哥伦比亚大学获得博士学位。我们现在要学习的卡尔曼滤波器，正是源于他的博士论文和1960年发表的论文《A New Approach to Linear Filtering and Prediction Problems》（线性滤波与预测问题的新方法）。如果对这编论文有兴趣，可以到这里的地址下载：  http://www.cs.unc.edu/~welch/media/pdf/Kalman1960.pdf%E3%80%82  。
简单来说，卡尔曼滤波器是一个“optimal recursive data processing algorithm（最优化自回归数据处理算法）”。对于解决很大部分的问题，他是最优，效率最高甚至是最有用的。他的广泛应用已经超过30年，包括机器人导航，控制，传感器数据融合甚至在军事方面的雷达系统以及导弹追踪等等。近年来更被应用于计算机图像处理，例如头脸识别，图像分割，图像边缘检测等等。

2．卡尔曼滤波器的介绍
（Introduction to the Kalman Filter）

为了可以更加容易的理解卡尔曼滤波器，这里会应用形象的描述方法来讲解，而不是像大多数参考书那样罗列一大堆的数学公式和数学符号。但是，他的5条公式是其核心内容。结合现代的计算机，其实卡尔曼的程序相当的简单，只要你理解了他的那5条公式。

在介绍他的5条公式之前，先让我们来根据下面的例子一步一步的探索。

假设我们要研究的对象是一个房间的温度。根据你的经验判断，这个房间的温度是恒定的，也就是下一分钟的温度等于现在这一分钟的温度（假设我们用一分钟来做时间单位）。假设你对你的经验不是100%的相信，可能会有上下偏差几度。我们把这些偏差看成是高斯白噪声（White Gaussian Noise），也就是这些偏差跟前后时间是没有关系的而且符合高斯分配（Gaussian Distribution）。另外，我们在房间里放一个温度计，但是这个温度计也不准确的，测量值会比实际值偏差。我们也把这些偏差看成是高斯白噪声。

好了，现在对于某一分钟我们有两个有关于该房间的温度值：你根据经验的预测值（系统的预测值）和温度计的值（测量值）。下面我们要用这两个值结合他们各自的噪声来估算出房间的实际温度值。

假如我们要估算k时刻的是实际温度值。首先你要根据k-1时刻的温度值，来预测k时刻的温度。因为你相信温度是恒定的，所以你会得到k时刻的温度预测值是跟k-1时刻一样的，假设是23度，同时该值的高斯噪声的偏差是5度（5是这样得到的：如果k-1时刻估算出的最优温度值的偏差是3，你对自己预测的不确定度是4度，他们平方相加再开方，就是5）。然后，你从温度计那里得到了k时刻的温度值，假设是25度，同时该值的偏差是4度。

由于我们用于估算k时刻的实际温度有两个温度值，分别是23度和25度。究竟实际温度是多少呢？相信自己还是相信温度计呢？究竟相信谁多一点，我们可以用他们的covariance来判断。因为Kg^2=5^2/(5^2+4^2)，所以Kg=0.78，我们可以估算出k时刻的实际温度值是：23+0.78*(25-23)=24.56度。可以看出，因为温度计的covariance比较小（比较相信温度计），所以估算出的最优温度值偏向温度计的值。

现在我们已经得到k时刻的最优温度值了，下一步就是要进入k+1时刻，进行新的最优估算。到现在为止，好像还没看到什么自回归的东西出现。对了，在进入k+1时刻之前，我们还要算出k时刻那个最优值（24.56度）的偏差。算法如下：((1-Kg)*5^2)^0.5=2.35。这里的5就是上面的k时刻你预测的那个23度温度值的偏差，得出的2.35就是进入k+1时刻以后k时刻估算出的最优温度值的偏差（对应于上面的3）。

就是这样，卡尔曼滤波器就不断的把covariance递归，从而估算出最优的温度值。他运行的很快，而且它只保留了上一时刻的covariance。上面的Kg，就是卡尔曼增益（Kalman Gain）。他可以随不同的时刻而改变他自己的值，是不是很神奇！

下面就要言归正传，讨论真正工程系统上的卡尔曼。

3． 卡尔曼滤波器算法
（The Kalman Filter Algorithm）

在这一部分，我们就来描述源于Dr Kalman 的卡尔曼滤波器。下面的描述，会涉及一些基本的概念知识，包括概率（Probability），随即变量（Random Variable），高斯或正态分配（Gaussian Distribution）还有State-space Model等等。但对于卡尔曼滤波器的详细证明，这里不能一一描述。

首先，我们先要引入一个离散控制过程的系统。该系统可用一个线性随机微分方程（Linear Stochastic Difference equation）来描述：
X(k)=A X(k-1)+B U(k)+W(k) 
再加上系统的测量值：
Z(k)=H X(k)+V(k) 
上两式子中，X(k)是k时刻的系统状态，U(k)是k时刻对系统的控制量。A和B是系统参数，对于多模型系统，他们为矩阵。Z(k)是k时刻的测量值，H是测量系统的参数，对于多测量系统，H为矩阵。W(k)和V(k)分别表示过程和测量的噪声。他们被假设成高斯白噪声(White Gaussian Noise)，他们的covariance 分别是Q，R（这里我们假设他们不随系统状态变化而变化）。

对于满足上面的条件(线性随机微分系统，过程和测量都是高斯白噪声)，卡尔曼滤波器是最优的信息处理器。下面我们来用他们结合他们的covariances 来估算系统的最优化输出（类似上一节那个温度的例子）。

首先我们要利用系统的过程模型，来预测下一状态的系统。假设现在的系统状态是k，根据系统的模型，可以基于系统的上一状态而预测出现在状态：
X(k|k-1)=A X(k-1|k-1)+B U(k) ……….. (1)
式(1)中，X(k|k-1)是利用上一状态预测的结果，X(k-1|k-1)是上一状态最优的结果，U(k)为现在状态的控制量，如果没有控制量，它可以为0。

到现在为止，我们的系统结果已经更新了，可是，对应于X(k|k-1)的covariance还没更新。我们用P表示covariance：
P(k|k-1)=A P(k-1|k-1) A’+Q ……… (2)
式(2)中，P(k|k-1)是X(k|k-1)对应的covariance，P(k-1|k-1)是X(k-1|k-1)对应的covariance，A’表示A的转置矩阵，Q是系统过程的covariance。式子1，2就是卡尔曼滤波器5个公式当中的前两个，也就是对系统的预测。

现在我们有了现在状态的预测结果，然后我们再收集现在状态的测量值。结合预测值和测量值，我们可以得到现在状态(k)的最优化估算值X(k|k)：
X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1)) ……… (3)
其中Kg为卡尔曼增益(Kalman Gain)：
Kg(k)= P(k|k-1) H’ / (H P(k|k-1) H’ + R) ……… (4)

到现在为止，我们已经得到了k状态下最优的估算值X(k|k)。但是为了要另卡尔曼滤波器不断的运行下去直到系统过程结束，我们还要更新k状态下X(k|k)的covariance：
P(k|k)=（I-Kg(k) H）P(k|k-1) ……… (5)
其中I 为1的矩阵，对于单模型单测量，I=1。当系统进入k+1状态时，P(k|k)就是式子(2)的P(k-1|k-1)。这样，算法就可以自回归的运算下去。

卡尔曼滤波器的原理基本描述了，式子1，2，3，4和5就是他的5 个基本公式。根据这5个公式，可以很容易的实现计算机的程序。

下面，我会用程序举一个实际运行的例子。。。
4． 简单例子
（A Simple Example）

这里我们结合第二第三节，举一个非常简单的例子来说明卡尔曼滤波器的工作过程。所举的例子是进一步描述第二节的例子，而且还会配以程序模拟结果。

根据第二节的描述，把房间看成一个系统，然后对这个系统建模。当然，我们见的模型不需要非常地精确。我们所知道的这个房间的温度是跟前一时刻的温度相同的，所以A=1。没有控制量，所以U(k)=0。因此得出：
X(k|k-1)=X(k-1|k-1) ……….. (6)
式子（2）可以改成：
P(k|k-1)=P(k-1|k-1) +Q ……… (7)

因为测量的值是温度计的，跟温度直接对应，所以H=1。式子3，4，5可以改成以下：
X(k|k)= X(k|k-1)+Kg(k) (Z(k)-X(k|k-1)) ……… (8)
Kg(k)= P(k|k-1) / (P(k|k-1) + R) ……… (9)
P(k|k)=（1-Kg(k)）P(k|k-1) ……… (10)

现在我们模拟一组测量值作为输入。假设房间的真实温度为25度，我模拟了200个测量值，这些测量值的平均值为25度，但是加入了标准偏差为几度的高斯白噪声（在图中为蓝线）。

为了令卡尔曼滤波器开始工作，我们需要告诉卡尔曼两个零时刻的初始值，是X(0|0)和P(0|0)。他们的值不用太在意，随便给一个就可以了，因为随着卡尔曼的工作，X会逐渐的收敛。但是对于P，一般不要取0，因为这样可能会令卡尔曼完全相信你给定的X(0|0)是系统最优的，从而使算法不能收敛。我选了X(0|0)=1度，P(0|0)=10。

该系统的真实温度为25度，图中用黑线表示。图中红线是卡尔曼滤波器输出的最优化结果（该结果在算法中设置了Q=1e-6，R=1e-1）。

一些网络资料

　　关于Kalman滤波器的理论,其数学公式太多,大家可以去查看一些这方面的文献.下面这篇文章对Kalman滤波做了个通俗易懂的介绍,通过文章举的例子可以宏观上理解一下该滤波器,很不错,推荐一看:http://www.cnblogs.com/feisky/archive/2009/11/09/1599247.html,

　　他的另一篇博客http://www.cnblogs.com/feisky/archive/2009/12/04/1617287.html

中介绍了opencv1.0版本的卡尔曼滤波的结构和函数定义等。

     另外博文：http://blog.csdn.net/onezeros/article/details/6318944将opencv中自带的kalman改装成了鼠标跟踪程序，可以一看。

     这篇博客http://blog.csdn.net/yang_xian521/article/details/7050398 对opencv中本身自带的Kalman例子讲解得很清楚。

 

　　kalman滤波简单介绍

     Kalman滤波理论主要应用在现实世界中个，并不是理想环境。主要是来跟踪的某一个变量的值，跟踪的依据是首先根据系统的运动方程来对该值做预测，比如说我们知道一个物体的运动速度，那么下面时刻它的位置按照道理是可以预测出来的，不过该预测肯定有误差，只能作为跟踪的依据。另一个依据是可以用测量手段来测量那个变量的值，当然该测量也是有误差的，也只能作为依据，不过这2个依据的权重比例不同。最后kalman滤波就是利用这两个依据进行一些列迭代进行目标跟踪的。

     在这个理论框架中，有2个公式一定要懂，即：

　　

　　

     第一个方程为系统的运动方程，第二个方程为系统的观测方程，学过自控原理中的现代控制理论的同学应该对这2个公式很熟悉。具体的相关理论本文就不做介绍了。

     Opencv目标版本中带有kalman这个类，可以使用它来完成一些跟踪目的。

 

　　下面来看看使用Kalman编程的主要步骤：

　　步骤一  ：

     Kalman这个类需要初始化下面变量：      

　　转移矩阵，测量矩阵，控制向量(没有的话，就是0)，过程噪声协方差矩阵，测量噪声协方差矩阵，后验错误协方差矩阵，前一状态校正后的值，当前观察值。 

　　步骤二：

　　调用kalman这个类的predict方法得到状态的预测值矩阵，预测状态的计算公式如下：

　　predicted state (x'(k)): x'(k)=A*x(k-1)+B*u(k)

　　其中x(k-1)为前一状态的校正值，第一个循环中在初始化过程中已经给定了，后面的循环中Kalman这个类内部会计算。A,B,u(k),也都是给定了的值。这样进过计算就得到了系统状态的预测值x'(k)了。 

　　步骤三：

　　调用kalman这个类的correct方法得到加入观察值校正后的状态变量值矩阵，其公式为：

　　corrected state (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))

　　其中x'(k)为步骤二算出的结果，z(k)为当前测量值，是我们外部测量后输入的向量。H为Kalman类初始化给定的测量矩阵。K(k)为Kalman增益，其计算公式为：

　　Kalman gain matrix (K(k)): K(k)=P'(k)*Ht*inv(H*P'(k)*Ht+R)

　　计算该增益所依赖的变量要么初始化中给定，要么在kalman理论中通过其它公式可以计算。

　　经过步骤三后，我们又重新获得了这一时刻的校正值，后面就不断循环步骤二和步骤三即可完成Kalman滤波过程。

 

　　实验部分

　　本次实验来源于opencv自带sample中的例子，该例子是用kalman来完成一个一维的跟踪，即跟踪一个不断变化的角度。在界面中表现为一个点在圆周上匀速跑，然后跟踪该点。看起来跟踪点是个二维的，其实转换成角度就是一维的了。

　　该代码中,有这么几句
　　KalmanFilter KF(2, 1, 0);
　　...
　　KF.transitionMatrix = *(Mat_<float>(2, 2) << 1, 1, 0, 1);
　　...

　　一直在想Mat_<float>(2, 2) << 1是什么意思呢?

　　如果是用：Mat_<float> A(2, 2);则这表示的是定义一个矩阵A。

　　但是Mat_<float>(2, 2)感觉又不是定义，貌似也不是数,既然不是数怎能左移呢?后面发现自己想错了.

　　Mat_<float>(2, 2) << 1, 1, 0, 1是一个整体,即往Mat_<float>(2, 2)的矩阵中赋值1,1,0,1;说白了就是给Mat矩阵赋初值，因为初值没什么规律，所以我们不能用zeros，ones等手段来赋值。比如运行下面语句时：

　　Mat a;

　　a = (Mat_<float>(2, 2) << 1, 1, 0, 1);

 　　cout<<a<<endl;

 　 其结果就为

　　[1,1;

　　0,1]

 

　　实验结果如下：

　　跟踪中某一时刻图1：

　　

 

　　跟踪中某一时刻图2：

　　

　　其中红色的短线条为目标点真实位置和目标点的测量位置的连线，黄色的短线为目标点真实位置和预测位置的连线，所以2中颜色相交中间那个点坐标为目标的真实坐标。

 

实验主要部分代码和注释(附录有工程code下载链接地址)：

Kalman.h:

#ifndef KALMAN_H
#define KALMAN_H

#include <QDialog>
#include <QTimer>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/video/video.hpp>

using namespace cv;

namespace Ui {
class kalman;
}

class kalman : public QDialog
{
    Q_OBJECT
    
public:
    explicit kalman(QWidget *parent = 0);
    ~kalman();
    
private slots:

    void on_startButton_clicked();

    void kalman_process();

    void on_closeButton_clicked();

private:
    Ui::kalman *ui;
    Mat img, state, processNoise, measurement;
    KalmanFilter KF;
    QTimer *timer;
    //给定圆心和周长，和圆周上的角度，求圆周上的坐标
    static inline Point calcPoint(Point2f center, double R, double angle)
    {
        //sin前面有个负号那是因为图片的顶点坐标在左上角
        return center + Point2f((float)cos(angle), (float)-sin(angle))*(float)R;
    }

};

#endif // KALMAN_H

 

Kalman.cpp:

#include "kalman.h"
#include "ui_kalman.h"
#include <iostream>

using namespace std;

kalman::kalman(QWidget *parent) :
    QDialog(parent),
    ui(new Ui::kalman)
{
    //在构造函数中定义变量不行？
    img.create(500, 500, CV_8UC3);
    cout<<img.rows<<endl;
    //状态维数2，测量维数1，没有控制量
    KF.init(2, 1, 0);
    //状态值，（角度，角速度）
    state.create(2, 1, CV_32F);
    processNoise.create(2, 1, CV_32F);
    measurement = Mat::zeros(1, 1, CV_32F);
    timer   = new QTimer(this);
    connect(timer, SIGNAL(timeout()), this, SLOT(kalman_process()));

    ui->setupUi(this);
    //这句必须放在ui->setupUi(this)后面，因为只有这样才能访问ui->textBrowser
    ui->textBrowser->setFixedSize(500, 500);
}

kalman::~kalman()
{
    delete ui;
}

void kalman::on_startButton_clicked()
{
    /*
      使用kalma步骤一
      下面语句到for前都是kalman的初始化过程，一般在使用kalman这个类时需要初始化的值有：
      转移矩阵，测量矩阵，过程噪声协方差，测量噪声协方差，后验错误协方差矩阵，
      前一状态校正后的值，当前观察值
    */

    //产生均值为0，标准差0.1的二维高斯列向量
    randn( state, Scalar::all(0), Scalar::all(0.1) );
    //transitionMatrix为类KalmanFilter中的一个变量，Mat型，是Kalman模型中的状态转移矩阵
    //转移矩阵为[1,1;0,1],2*2维的
    KF.transitionMatrix = *(Mat_<float>(2, 2) << 1, 1, 0, 1);

    //函数setIdentity是给参数矩阵对角线赋相同值，默认对角线值值为1
    setIdentity(KF.measurementMatrix);
    //系统过程噪声方差矩阵
    setIdentity(KF.processNoiseCov, Scalar::all(1e-5));
    //测量过程噪声方差矩阵
    setIdentity(KF.measurementNoiseCov, Scalar::all(1e-1));
    //后验错误估计协方差矩阵
    setIdentity(KF.errorCovPost, Scalar::all(1));
    //statePost为校正状态，其本质就是前一时刻的状态
    randn(KF.statePost, Scalar::all(0), Scalar::all(0.1));
    //设置定时器时间,默认情况下其该定时器可无限定时，即其SingleShot为false
    //如果将其设置为true，则该定时器只能定时一次
    //因此这里是每个33ms就去执行一次kalman处理函数
    timer->start(33);
 //   timer->setSingleShot( true );

}


void kalman::kalman_process()
{
    Point2f center(img.cols*0.5f, img.rows*0.5f);
    float R = img.cols/3.f;
    //state中存放起始角，state为初始状态
    double stateAngle = state.at<float>(0);
    Point statePt = calcPoint(center, R, stateAngle);


    /*
      使用kalma步骤二
      调用kalman这个类的predict方法得到状态的预测值矩阵
    */
    //predicted state (x'(k)): x'(k)=A*x(k-1)+B*u(k)
    //其中x(k-1)为前面的校正状态，因此这里是用校正状态来预测的
    //而校正状态corrected state (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
    //又与本时刻的预测值和校正值有关系
    Mat prediction = KF.predict();
    //用kalman预测的是角度
    double predictAngle = prediction.at<float>(0);
    Point predictPt = calcPoint(center, R, predictAngle);

    randn( measurement, Scalar::all(0), Scalar::all(KF.measurementNoiseCov.at<float>(0)));

    // generate measurement
    //带噪声的测量
    measurement += KF.measurementMatrix*state;
   // measurement += KF.measurementMatrix*prediction;

    double measAngle = measurement.at<float>(0);
    Point measPt = calcPoint(center, R, measAngle);

    // plot points
    //这个define语句是画2条线段(线长很短)，其实就是画一个“X”叉符号
    #define drawCross( center, color, d )                                 \
        line( img, Point( center.x - d, center.y - d ),                \
                     Point( center.x + d, center.y + d ), color, 1, CV_AA, 0); \
        line( img, Point( center.x + d, center.y - d ),                \
                     Point( center.x - d, center.y + d ), color, 1, CV_AA, 0 )

    img = Scalar::all(0);
    //状态坐标白色
    drawCross( statePt, Scalar(255,255,255), 3 );
    //测量坐标蓝色
    drawCross( measPt, Scalar(0,0,255), 3 );
    //预测坐标绿色
    drawCross( predictPt, Scalar(0,255,0), 3 );
    //真实值和测量值之间用红色线连接起来
    line( img, statePt, measPt, Scalar(0,0,255), 3, CV_AA, 0 );
    //真实值和估计值之间用黄色线连接起来
    line( img, statePt, predictPt, Scalar(0,255,255), 3, CV_AA, 0 );


    /*
      使用kalma步骤三
      调用kalman这个类的correct方法得到加入观察值校正后的状态变量值矩阵
    */
    //虽然该函数有返回值Mat，但是调用该函数校正后，其校正值已经保存在KF的statePost
    //中了，corrected state (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
    KF.correct(measurement);

    randn( processNoise, Scalar(0), Scalar::all(sqrt(KF.processNoiseCov.at<float>(0, 0))));
    //不加噪声的话就是匀速圆周运动，加了点噪声类似匀速圆周运动，因为噪声的原因，运动方向可能会改变
    state = KF.transitionMatrix*state + processNoise;

    imwrite("../kalman/img.jpg", img);
    ui->textBrowser->clear();
    //ui->textBrowser->setFixedSize(img.cols, img.rows);
    ui->textBrowser->append("<img src=../kalman/img.jpg>");
}


void kalman::on_closeButton_clicked()
{
    close();
}

 

　　在用Qt编程中碰到了下面的疑问 

　　疑问1：

　　Qt界面编程中，由于构造函数中不能定义全局变量，我们需要把全局变量定义在内的内部(即在头文件中定义)，那么在使用类似于opencv中这些自带初始值赋值的方法是不是就不能那样使用了呢？比如说Mat img(500, 500, CV_8UC3);因为在头文件中的定义不能同时初始化，在源文件中又不能定义。难道我们一定要将初始化和定义分开写？

     查了下资料，基本上只能分开写了。其实类似opencv等开源库中的函数都考虑到了这一点。如果是用c编程，其全局变量可以直接这样赋值，Mat img(500, 500, CV_8UC3);如果是有关界面的c++编程，则Mat会提供另外一个函数来初始化的，Mat这里提供的是create函数，img.create(500, 500, CV_8UC3);其它函数类似。

 

　　疑问2：

　　Qt界面编程中，当我们按下一个按钮时，需要在这个按钮的槽函数里面实现一个死循环的功能，比如说让界面中一直显示一个运动的圆，由于该点在运动，所以需要代码不断的画圆，因此用了死循环。而当我们按下该界面中的另一个按钮，比如退出程序按钮时，因为前一个按钮中一直在响应，所以无法响应我们的退出按钮请求，遇到这种情况该怎么解决呢？

　　答案首先能肯定的是，一般情况下按钮响应槽函数中不宜使用死循环语句，否则外面函数无法响应。网上说一般解决这种问题用多线程编程技术比较好（这里我没有去试过，因为不了解多线程技术，当然了，这个以后有时间一定要去学下的）。我这里采用了另外一种方法即利用的定时器功能，触发定时器槽函数，每隔一段时间执行一下需要执行的函数。具体见代码中。

     上面2个疑问是暂时的替代方案，大家有更好的可以提出来贡献下，谢谢。

 

　　总结：

　　kalman应用比较广，虽然学习它的理论都是数学公式，不过我们可以先学会在程序中怎么使用它，在慢慢去看理论，2者结合，这样效果会好很多。

首先来看一下OpenCV中关于Kalman滤波的结构和函数定义

CvKalman

Kalman 滤波器状态

typedef struct CvKalman
{
    int MP;                     /* 测量向量维数 */
    int DP;                     /* 状态向量维数 */
    int CP;                     /* 控制向量维数 */

    /* 向后兼容字段 */
#if 1
    float* PosterState;         /* =state_pre->data.fl */
    float* PriorState;          /* =state_post->data.fl */
    float* DynamMatr;           /* =transition_matrix->data.fl */
    float* MeasurementMatr;     /* =measurement_matrix->data.fl */
    float* MNCovariance;        /* =measurement_noise_cov->data.fl */
    float* PNCovariance;        /* =process_noise_cov->data.fl */
    float* KalmGainMatr;        /* =gain->data.fl */
    float* PriorErrorCovariance;/* =error_cov_pre->data.fl */
    float* PosterErrorCovariance;/* =error_cov_post->data.fl */
    float* Temp1;               /* temp1->data.fl */
    float* Temp2;               /* temp2->data.fl */
#endif

    CvMat* state_pre;           /* 预测状态 (x'(k)): 
                                    x(k)=A*x(k-1)+B*u(k) */
    CvMat* state_post;          /* 矫正状态 (x(k)):
                                    x(k)=x'(k)+K(k)*(z(k)-H*x'(k)) */
    CvMat* transition_matrix;   /* 状态传递矩阵 state transition matrix (A) */
    CvMat* control_matrix;      /* 控制矩阵 control matrix (B)
                                   (如果没有控制，则不使用它)*/
    CvMat* measurement_matrix;  /* 测量矩阵 measurement matrix (H) */
    CvMat* process_noise_cov;   /* 过程噪声协方差矩阵
                                        process noise covariance matrix (Q) */
    CvMat* measurement_noise_cov; /* 测量噪声协方差矩阵
                                          measurement noise covariance matrix (R) */
    CvMat* error_cov_pre;       /* 先验误差计协方差矩阵
                                        priori error estimate covariance matrix (P'(k)):
                                     P'(k)=A*P(k-1)*At + Q)*/
    CvMat* gain;                /* Kalman 增益矩阵 gain matrix (K(k)):
                                    K(k)=P'(k)*Ht*inv(H*P'(k)*Ht+R)*/
    CvMat* error_cov_post;      /* 后验错误估计协方差矩阵
                                        posteriori error estimate covariance matrix (P(k)):
                                     P(k)=(I-K(k)*H)*P'(k) */
    CvMat* temp1;               /* 临时矩阵 temporary matrices */
    CvMat* temp2;
    CvMat* temp3;
    CvMat* temp4;
    CvMat* temp5;
}
CvKalman;

结构 CvKalman 用来保存 Kalman 滤波器状态。它由函数 cvCreateKalman 创建，由函数f cvKalmanPredict 和 cvKalmanCorrect 更新，由 cvReleaseKalman 释放. 通常该结构是为标准 Kalman 所使用的 (符号和公式都借自非常优秀的 Kalman 教程 [Welch95]):

系统运动方程：

系统观测方程：

其中:

x_k(x_{k − 1}) - 系统在时刻 k (k-1) 的状态向量 （state of the system at the moment k (k-1)）

z_k - 在时刻 k 的系统状态测量向量 （measurement of the system state at the moment k）

u_k - 应用于时刻 k 的外部控制 (external control applied at the moment k)

w_k 和  v_k 分别为正态分布的运动和测量噪声

p(w) ~ N(0,Q)

p(v) ~ N(0,R),

即,

Q - 运动噪声的相关矩阵，常量或变量

R - 测量噪声的相关矩阵，常量或变量

对标准 Kalman 滤波器，所有矩阵: A, B, H, Q 和 R 都是通过 cvCreateKalman 在分配结构 CvKalman 时初始化一次。但是，同样的结构和函数，通过在当前系统状态邻域中线性化扩展 Kalman 滤波器方程，可以用来模拟扩展 Kalman 滤波器，在这种情况下， A, B, H (也许还有 Q 和 R) 在每一步中都被更新。

CreateKalman

分配 Kalman 滤波器结构

CvKalman* cvCreateKalman( int dynam_params, int measure_params, int control_params=0 );

dynam_params

状态向量维数

measure_params

测量向量维数

control_params

控制向量维数

函数 cvCreateKalman 分配 CvKalman 以及它的所有矩阵和初始参数

ReleaseKalman

释放 Kalman 滤波器结构

void cvReleaseKalman( CvKalman** kalman );

kalman

指向 Kalman 滤波器结构的双指针

函数 cvReleaseKalman 释放结构 CvKalman 和里面所有矩阵

KalmanPredict

估计后来的模型状态

const CvMat* cvKalmanPredict( CvKalman* kalman, const CvMat* control=NULL );
#define cvKalmanUpdateByTime cvKalmanPredict

kalman

Kalman 滤波器状态

control

控制向量 (uk), 如果没有外部控制 (control_params=0) 应该为 NULL

函数 cvKalmanPredict 根据当前状态估计后来的随机模型状态，并存储于 kalman->state_pre:

,

其中

x'_k 是预测状态 (kalman->state_pre),

x_{k − 1} 是前一步的矫正状态 (kalman->state_post)，应该在开始的某个地方初始化，即缺省为零向量，

u_k 是外部控制(control 参数),

P'_k 是先验误差相关矩阵 (kalman->error_cov_pre)

P_{k − 1} 是前一步的后验误差相关矩阵(kalman->error_cov_post),应该在开始的某个地方初始化，即缺省为单位矩阵.

函数返回估计得到的状态值

KalmanCorrect

调节模型状态

const CvMat* cvKalmanCorrect( CvKalman* kalman, const CvMat* measurement );
#define cvKalmanUpdateByMeasurement cvKalmanCorrect

kalman

被更新的 Kalman 结构的指针

measurement

指向测量向量的指针，向量形式为 CvMat

函数 cvKalmanCorrect 在给定的模型状态的测量基础上，调节随机模型状态：

其中

z_k - 给定测量(mesurement parameter)

K_k - Kalman "增益" 矩阵

函数存储调节状态到 kalman->state_post 中并且输出时返回它。

 

下面实现了一个简单的跟踪小程序，直接给出程序源码：

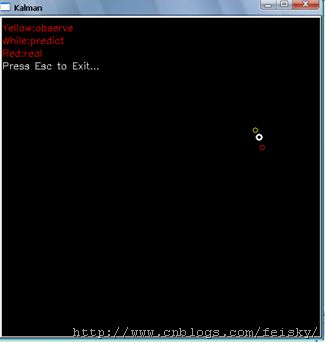
void CSLAMApplicationView::OnEKFTracking()
{
	// Initialize Kalman filter object, window, number generator, etc
	cvNamedWindow( "Kalman", 1 );//创建窗口，当为的时候，表示窗口大小自动设定
	CvRandState rng;
	cvRandInit( &rng, 0, 1, -1, CV_RAND_UNI );/* CV_RAND_UNI 指定为均匀分布类型、随机数种子为-1 */

	IplImage* img = cvCreateImage( cvSize(500,500), 8, 3 );
	CvKalman* kalman = cvCreateKalman( 2, 1, 0 );/*状态向量为维，观测向量为维，无激励输入维*/

	// State is phi, delta_phi - angle and angular velocity
	// Initialize with random guess
	CvMat* x_k = cvCreateMat( 2, 1, CV_32FC1 );/*创建行列、元素类型为CV_32FC1，元素为位单通道浮点类型矩阵。*/
	cvRandSetRange( &rng, 0, 0.1, 0 );/*设置随机数范围，随机数服从正态分布，均值为，均方差为.1，通道个数为*/
	rng.disttype = CV_RAND_NORMAL;
	cvRand( &rng, x_k ); /*随机填充数组*/

	// Process noise
	CvMat* w_k = cvCreateMat( 2, 1, CV_32FC1 );

	// Measurements, only one parameter for angle
	CvMat* z_k = cvCreateMat( 1, 1, CV_32FC1 );/*定义观测变量*/
	cvZero( z_k ); /*矩阵置零*/

	// Transition matrix F describes model parameters at and k and k+1
	const float F[] = { 1, 1, 0, 1 }; /*状态转移矩阵*/
	memcpy( kalman->transition_matrix->data.fl, F, sizeof(F));
	/*初始化转移矩阵，行列，具体见CvKalman* kalman = cvCreateKalman( 2, 1, 0 );*/

	// Initialize other Kalman parameters
	cvSetIdentity( kalman->measurement_matrix, cvRealScalar(1) );/*观测矩阵*/
	cvSetIdentity( kalman->process_noise_cov, cvRealScalar(1e-5) );/*过程噪声*/
	cvSetIdentity( kalman->measurement_noise_cov, cvRealScalar(1e-1) );/*观测噪声*/
	cvSetIdentity( kalman->error_cov_post, cvRealScalar(1) );/*后验误差协方差*/

	// Choose random initial state
	cvRand( &rng, kalman->state_post );/*初始化状态向量*/

	// Make colors
	CvScalar yellow = CV_RGB(255,255,0);/*依次为红绿蓝三色*/
	CvScalar white = CV_RGB(255,255,255);
	CvScalar red = CV_RGB(255,0,0);

	while( 1 ){
		// Predict point position
		const CvMat* y_k = cvKalmanPredict( kalman, 0 );/*激励项输入为*/

		// Generate Measurement (z_k)
		cvRandSetRange( &rng, 0, sqrt( kalman->measurement_noise_cov->data.fl[0] ), 0 );/*设置观测噪声*/	
		cvRand( &rng, z_k );
		cvMatMulAdd( kalman->measurement_matrix, x_k, z_k, z_k );

		// Update Kalman filter state
		cvKalmanCorrect( kalman, z_k );

		// Apply the transition matrix F and apply "process noise" w_k
		cvRandSetRange( &rng, 0, sqrt( kalman->process_noise_cov->data.fl[0] ), 0 );/*设置正态分布过程噪声*/
		cvRand( &rng, w_k );
		cvMatMulAdd( kalman->transition_matrix, x_k, w_k, x_k );

		// Plot Points
		cvZero( img );/*创建图像*/
		// Yellow is observed state 黄色是观测值
		//cvCircle(IntPtr, Point, Int32, MCvScalar, Int32, LINE_TYPE, Int32)
		//对应于下列其中，shift为数据精度
		//cvCircle(img, center, radius, color, thickness, lineType, shift)
		//绘制或填充一个给定圆心和半径的圆
		cvCircle( img, 
			cvPoint( cvRound(img->width/2 + img->width/3*cos(z_k->data.fl[0])),
			cvRound( img->height/2 - img->width/3*sin(z_k->data.fl[0])) ), 
			4, yellow );
		// White is the predicted state via the filter
		cvCircle( img, 
			cvPoint( cvRound(img->width/2 + img->width/3*cos(y_k->data.fl[0])),
			cvRound( img->height/2 - img->width/3*sin(y_k->data.fl[0])) ), 
			4, white, 2 );
		// Red is the real state
		cvCircle( img, 
			cvPoint( cvRound(img->width/2 + img->width/3*cos(x_k->data.fl[0])),
			cvRound( img->height/2 - img->width/3*sin(x_k->data.fl[0])) ),
			4, red );
		CvFont font;
		cvInitFont(&font,CV_FONT_HERSHEY_SIMPLEX,0.5f,0.5f,0,1,8);
		cvPutText(img,"Yellow:observe",cvPoint(0,20),&font,cvScalar(0,0,255));
		cvPutText(img,"While:predict",cvPoint(0,40),&font,cvScalar(0,0,255));
		cvPutText(img,"Red:real",cvPoint(0,60),&font,cvScalar(0,0,255));
		cvPutText(img,"Press Esc to Exit...",cvPoint(0,80),&font,cvScalar(255,255,255));
		cvShowImage( "Kalman", img );		

		// Exit on esc key
		if(cvWaitKey(100) == 27) 
			break;
	}
	cvReleaseImage(&img);/*释放图像*/
	cvReleaseKalman(&kalman);/*释放kalman滤波对象*/
	cvDestroyAllWindows();/*释放所有窗口*/
}

参考：opencv中文论坛

 

另外我的程序还实现了图片的打开和保存功能，具体也是参考了论坛的MFC中应用Opencv的帖子，不过我稍微改进了一下，不进行图片的缩放，显示源图像的大小：

首先是doc类定义CImage* m_Image;

CSLAMApplicationDoc::CSLAMApplicationDoc()
{
	m_Image=NULL;
}

CSLAMApplicationDoc::~CSLAMApplicationDoc()
{
	if(m_Image!=NULL)
	{
		m_Image->Destroy();
		delete m_Image;
	}
}

// CSLAMApplicationDoc 命令

BOOL CSLAMApplicationDoc::OnOpenDocument(LPCTSTR lpszPathName)
{
	if (!CDocument::OnOpenDocument(lpszPathName))
		return FALSE;

	// TODO:  Add your specialized creation code here
	m_Image=new CImage();
	m_Image->Load(lpszPathName);

	return TRUE;
}

BOOL CSLAMApplicationDoc::OnSaveDocument(LPCTSTR lpszPathName)
{
	// TODO: Add your specialized code here and/or call the base class
	m_Image->Save(lpszPathName);

	return CDocument::OnSaveDocument(lpszPathName);
}
// CSLAMApplicationView 绘制

void CSLAMApplicationView::OnDraw(CDC* pDC)
{
	CSLAMApplicationDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;

	// TODO: 在此处为本机数据添加绘制代码
	CImage *img=pDoc->m_Image;
	if(img!=NULL)
	{
		CRect r;
		GetClientRect (&r);
		if(img->Width()<r.Width())
		{
			r.right=img->Width();
		}
		if(img->Height()<r.Height())
		{
			r.bottom=img->Height();
		}
		pDoc->m_Image->DrawToHDC(pDC->GetSafeHdc(),r);
	}