数据结构之图
学完图 只有一个感觉 ,术语真的好多。
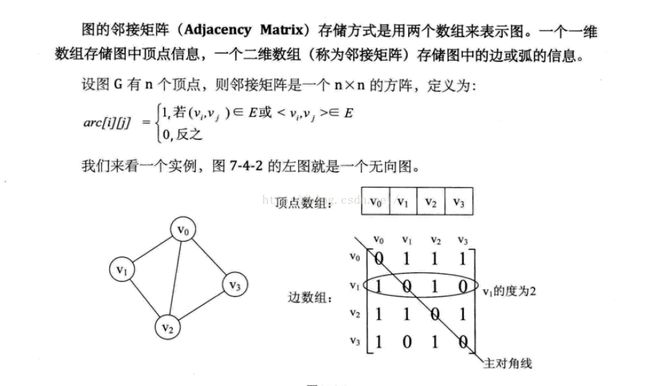
图是一种非线性结构。图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有n(n-1)/2条边。
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n(n-1)条边。
在无向图G中,如果从顶点v到v‘有路径,则称v和v’是连通的。如果对于图中的任意两个结点都是连通的,则称G是连通图。
在有向图中同理。
图的存储
1)邻接矩阵:
若图G是一个带权图,则把所有的1换成边的权值。
2)邻接表:
邻接表是对图中的每个顶点建立一个邻接关系的单链表,并把他们的表头指针用一维数组存储的一种图的表示方法。邻结表中的每个结点用来存储以该顶点为端点或起点的一条边的信息,因而叫边结点。边结点通常包含三个域:邻接点域(用来存储顶点Vi的一个邻接顶点Vj的序号j);权值域(用来存储ij的权值);链接域(用来链接邻接表的下一个结点)
3)边集数组
边集数组是利用一维数组存储图中所有边的一种图的表示方法,包含起点域,终点域,权值。
package org.graph.cn;
public interface GraphADT {
/***
* 根据边集数组参数d建立一个图
* @param d 边集数组
*/
void create(EdgeElement[] d);
/**
* 返回图的类型
*/
int graphType();
/***
* 返回图中的顶点数
*/
int vertices();
/**
* 返回图中的边数
*/
int edges();
/***
* 从图中查找一条边(i,j)是否存在
* @param i
* @param j
* @return
*/
boolean find(int i,int j);
/**
* 从图中插入一条边
* @param theEdge 插入的边
*/
void putEdge(EdgeElement theEdge);
/***
* 从图中删除一条边(i,j)
* @param i
* @param j
*/
void removeEdge(int i,int j);
/***
* 返回顶点i的度
* @param i
* @return
*/
int degree(int i);
/**
* 返回顶点i的入度
* @param i
* @return
*/
int inDegree(int i);
/**
* 返回顶点i的出度
* @param i
* @return
*/
int outDegree(int i);
/***
* 以图的顶点集和边集的形式输出一个图
*/
void outPut();
/***
* 从顶点v开始深度优先搜索遍历图
* @param v
*/
void depthFirstSearch(int v);
/***
* 从顶点v开始广度优先搜索遍历图
* @param v
*/
void breadthFirstSearch(int v);
}
package org.graph.cn;
/**
* 定义边集数组中的元素类型
* @author Administrator
*
*/
public class EdgeElement {
int fromvex; //边的起点域
int endvex; //边的终点域
int weight; //边的权值域,假定为整型,对于无权图 ,权值可以为1
public EdgeElement(int v1,int v2) {
// TODO Auto-generated constructor stub
fromvex=v1;
endvex=v2;
weight=1;
}
public EdgeElement(int v1,int v2,int wgt) {
// TODO Auto-generated constructor stub
fromvex=v1;
endvex=v2;
weight=wgt;
}
}
package org.graph.cn;
import java.text.DateFormatSymbols;
import org.queen.cn.SequenceQueen;
/***
* 图的邻接矩阵存储类
* @author Administrator
*
*/
public class AdjacencyGraph implements GraphADT{
private final int MaxValue=1000; //一个不存在的变得使用的权值
private int n; //图的顶点数
private int e; //图的边数
private int type; //图的类型 0-->无向无权图,1-->无向有权图,2-->有向无权图,3-->有向有权图
private int[][] a; //图的邻接矩阵,假定元素类型为int
public int MaxValue(){ //返回最大值常量 带权图中的边不存在时的常量
return MaxValue;
}
public int[][] getArray(){ //返回邻接矩阵
return a;
}
/***
*
* @param n 顶点数
* @param t 图的类型
*/
public AdjacencyGraph(int n,int t) {
// TODO Auto-generated constructor stub
if(n<1||t<0||t>3){
System.out.println("初始化图的参数值出错");
}
this.n=n;
e=0;
type=t;
a=new int[n][n]; //给表示邻接矩阵的数组a分配存储空间
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(i==j){
a[i][j]=0; //对角线的元素被初始化为0
}else if(type==0||type==2){
a[i][j]=0; //对无权图初始化为0
}else{
a[i][j]=MaxValue;
}
}
}
}
@Override
public void create(EdgeElement[] d) {
// TODO Auto-generated method stub
int i;
for(i=0;i<d.length;i++){
if(d[i]==null){
break;
}
int v1,v2;
v1=d[i].fromvex;
v2=d[i].endvex;
if(v1<0||v1>n-1||v2<0||v2>n-1||v1==v2){
System.out.println("边的顶点序号无效");
}
if(type==0){
a[v1][v2]=a[v2][v1];
}else if(type==1){
a[v1][v2]=a[v2][v1]=d[i].weight;
}else if(type==2){
a[v1][v2]=1;
}else{
a[v1][v2]=d[i].weight;
}
}
e=i;
}
@Override
public int graphType() {
// TODO Auto-generated method stub
return type;
}
@Override
public int vertices() {
// TODO Auto-generated method stub
return n;
}
@Override
public int edges() {
// TODO Auto-generated method stub
return e;
}
@Override
public boolean find(int i, int j) {
// TODO Auto-generated method stub
if(i<0||i>n-1||j<0||j>n-1||i==j){
System.out.println("边的顶点序号无效");
}
if(a[i][j]!=0 && a[i][j]!=MaxValue){
return true;
}else{
return false;
}
}
@Override
public void putEdge(EdgeElement theEdge) {
// TODO Auto-generated method stub
int v1,v2;
v1=theEdge.fromvex;
v2=theEdge.endvex;
if(v1<0||v1>n-1||v2<0||v2>n-1||v1==v2){
System.out.println("边的顶点序号无效");
}
if(a[v1][v2]==0||a[v1][v2]==MaxValue){
e++;
}
if(type==0||type==1){
if(type==0){
a[v1][v2]=a[v2][v1]=1;
}else{
a[v1][v2]=a[v2][v1]=theEdge.weight;
}
}else{
if(type==2){
a[v1][v2]=1;
}else{
a[v1][v2]=a[v2][v1]=theEdge.weight;
}
}
}
@Override
public void removeEdge(int i, int j) {
// TODO Auto-generated method stub
if(i<0||i>n-1||j<0||j>n-1||i==j){
System.out.println("边的顶点序号无效");
}
if(a[i][j]==0||a[i][j]==MaxValue){
System.out.println("要删除的边不存在");
}
if(type==0){ //删除无向无权图的边
a[i][j]=a[j][i]=0;
}else if(type==1){ //删除无向有权图的边
a[i][j]=a[j][i]=MaxValue;
}else if(type==2){ //删除有向无权图的边
a[i][j]=0;
}else{ //删除有向有权图的边
a[i][j]=MaxValue;
}
e--;
}
@Override
public int degree(int i) {
// TODO Auto-generated method stub
if(i<0||i>n-1){
System.out.println("参数的顶点序号值无效");
}
int k=0; //k统计顶点i的度数
if(type==0||type==1){
for(int j=0;j<n;j++){
if(a[i][j]!=0 && a[j][i]!=MaxValue){
k++;
}
}
return k;
}else{
return inDegree(i)+outDegree(i);
}
}
@Override
public int inDegree(int i) {
// TODO Auto-generated method stub
if(i<0||i>n-1){
System.out.println("参数的顶点序号值无效");
}
if(type==0||type==1){
return -1;
}
int k=0;
for(int j=0;j<n;j++){
if(a[j][i]!=0 && a[j][i]!=MaxValue){
k++;
}
}
return k;
}
@Override
public int outDegree(int i) {
// TODO Auto-generated method stub
if(i<0||i>n-1){
System.out.println("参数的顶点序号值无效");
}
if(type==0||type==1){
return -1;
}
int k=0;
for(int j=0;j<n;j++){
if(a[i][j]!=0 && a[i][j]!=MaxValue){
k++;
}
}
return k;
}
@Override
public void outPut() {
// TODO Auto-generated method stub
int i,j;
System.out.print("V={");
for(i=0;i<n-1;i++){
System.out.print(i+", ");
}
System.out.println(n-1+"}"); //输出顶点集结束
System.out.print("E={");
if(type==0||type==2){
for(i=0;i<n;i++){
for(j=0;j<n;j++){
if(a[i][j]!=0 && a[i][j]!=MaxValue){
if(type==0){
if(i<j){
System.out.print("("+i+","+j+")");
}else{
System.out.print("<"+i+","+j+">,");
}
}
}
}
}
}else{
for(i=0;i<n;i++){
for(j=0;j<n;j++){
if(a[i][j]!=0&&a[i][j]!=MaxValue){
if(type==1){
if(i<j){
System.out.println("("+i+","+j+")"+a[i][j]+",");
}else{
System.out.print("<"+i+","+j+">"+a[i][j]+",");
}
}
}
}
}
}
System.out.println("}");
}
@Override
public void depthFirstSearch(int v) {
// TODO Auto-generated method stub
boolean[] visited=new boolean[n];
for(int i=0;i<n;i++){
visited[i]=false; //每一个元素都被初始化为false
}
dfs(v, visited);
System.out.println();
}
private void dfs(int i,boolean[] visited){
//从初始点Vi出发深度优先搜索
System.out.print(i+" "); //访问的顶点Vi以输出该顶点的序号代之
visited[i]=true; //标记该顶点已经被访问过了
for(int j=0;j<n;j++){
if(a[i][j]!=0 && a[i][j]!=MaxValue && !visited[j]){
dfs(j, visited);
}
}
}
@Override
public void breadthFirstSearch(int v) {
// TODO Auto-generated method stub
boolean[] visited=new boolean[n];
for(int i=0;i<n;i++){
visited[i]=false;
}
bfs(v, visited);
System.out.println();
}
private void bfs(int i,boolean[] visited){
SequenceQueen q=new SequenceQueen();
System.out.print(i+" ");
visited[i]=true;
q.enter(i);
while(!q.isEmpty()){
int k=(int) q.leave();
for(int j=0;j<n;j++){
if(a[k][j]!=0 && a[k][j]!=MaxValue && !visited[j]){
System.out.print(j+" ");
visited[j]=true;
q.enter(j);
}
}
}
}
}
在这里暂时只有用边集数组表示的图,下次有时间补上其他的代码。