hdoj 3338 Kakuro Extension 【行进列出 最大流】
Kakuro ExtensionTime Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1432 Accepted Submission(s): 484 Special Judge
Problem Description
If you solved problem like this, forget it.Because you need to use a completely different algorithm to solve the following one.
Kakuro puzzle is played on a grid of "black" and "white" cells. Apart from the top row and leftmost column which are entirely black, the grid has some amount of white cells which form "runs" and some amount of black cells. "Run" is a vertical or horizontal maximal one-lined block of adjacent white cells. Each row and column of the puzzle can contain more than one "run". Every white cell belongs to exactly two runs — one horizontal and one vertical run. Each horizontal "run" always has a number in the black half-cell to its immediate left, and each vertical "run" always has a number in the black half-cell immediately above it. These numbers are located in "black" cells and are called "clues".The rules of the puzzle are simple: 1.place a single digit from 1 to 9 in each "white" cell 2.for all runs, the sum of all digits in a "run" must match the clue associated with the "run" Given the grid, your task is to find a solution for the puzzle. 
Picture of the first sample input Picture of the first sample output
Input
The first line of input contains two integers n and m (2 ≤ n,m ≤ 100) — the number of rows and columns correspondingly. Each of the next n lines contains descriptions of m cells. Each cell description is one of the following 7-character strings:
.......— "white" cell; XXXXXXX— "black" cell with no clues; AAA\BBB— "black" cell with one or two clues. AAA is either a 3-digit clue for the corresponding vertical run, or XXX if there is no associated vertical run. BBB is either a 3-digit clue for the corresponding horizontal run, or XXX if there is no associated horizontal run. The first row and the first column of the grid will never have any white cells. The given grid will have at least one "white" cell.It is guaranteed that the given puzzle has at least one solution.
Output
Print n lines to the output with m cells in each line. For every "black" cell print '_' (underscore), for every "white" cell print the corresponding digit from the solution. Delimit cells with a single space, so that each row consists of 2m-1 characters.If there are many solutions, you may output any of them.
Sample Input
Sample Output
|
处理限流1~9时花了很长时间，前前后后花了很长时间才A的，挺艰辛的 o(╯□╰)o
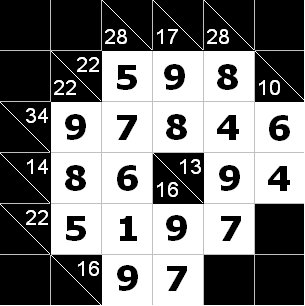
题意：给你一个N*M的方格，每个格子里面存入7个字符组成的字符串AAA\BBB。其中AAA为列值，BBB为行值。若全为 . 表示该格是白格，若AAA(BBB)为字符串XXX，表示该格是黑色的，但没有相应的列值(行值)。现在要求——每一行中黑格的行值和等于白格的数值和，每一列中黑格的列值和等于白格的数值和。让你用数字1~9填满所有的白格（当然白格数字至少为1）。
这种求可行解的题目，果断最大流来跑啊。
建图不是很难想，主要在于处理1~9的限流，因为这里WA了2个多小时。。。
重点：预处理所有行、列，用Xn、Yn分别记录行号、列号，设置数组xval[]（yval[]）记录当前行（列）所记录的数值。用numx[][]、numy[][]分别记录白格对应的行号、列号。相应的，为了保证流量在1~9范围，每遇到一个白格，就把它所对应的行号num[][]、列号numy[][]所记录的数值减一。
建图：设置超级源点S，超级汇点T
1，S向所有行建边，容量为当前行号对应的数值；
2，所有列向T建边，容量为当前列号对应的数值；
3，对于每个白格，由numx[][] 指向 numy[][]，容量为8；
跑完最大流后，边numx[i][j] -> numy[i][j]的流量 + 1就是白格（i, j）的数值。
AC代码：注释部分的建图是错误的。。。
难道<algorithm>里面还有xn和yn？无脑CE一次，把xn和yn换大写才AC。
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define MAXN 10000+300
#define MAXM 400000+10
#define INF 0x3f3f3f3f
using namespace std;
struct Edge
{
int from, to, cap, flow, next;
};
Edge edge[MAXM];
int head[MAXN], edgenum;
int dist[MAXN];
bool vis[MAXN];
int cur[MAXN];
int N, M, S, T;
struct ME{
int h, v;//水平值 和 垂直值
};
ME Map[110][110];
int Count(char *s, int f)
{
int sum = 0;
for(int i = f; i < f+3; i++)
sum = sum * 10 + s[i] - '0';
return sum;
}
void init(){
edgenum = 0;
memset(head, -1, sizeof(head));
}
void addEdge(int u, int v, int w){
Edge E1 = {u, v, w, 0, head[u]};
edge[edgenum] = E1;
head[u] = edgenum++;
Edge E2 = {v, u, 0, 0, head[v]};
edge[edgenum] = E2;
head[v] = edgenum++;
}
int point(int x, int y){
return (x-1)*M+y;
}
void input()
{
char str[10];
for(int i = 1; i <= N; i++)
{
for(int j = 1; j <= M; j++)
{
scanf("%s", str);
if(str[0] == '.')
Map[i][j].h = Map[i][j].v = -1;//白色
else if(str[0] == 'X')
{
if(str[4] == 'X')
Map[i][j].h = Map[i][j].v = -2;//空
else
{
Map[i][j].v = -2;
Map[i][j].h = Count(str, 4);
}
}
else
{
if(str[4] == 'X')
{
Map[i][j].h = -2;
Map[i][j].v = Count(str, 0);
}
else
{
Map[i][j].h = Count(str, 4);
Map[i][j].v = Count(str, 0);
}
}
}
}
}
//void getMap()
//{
// S = 0, T = N*M+1;
// init();
// int sum;
// int cnt;//记录白格数目
// //对行处理
// for(int i = 1; i <= N; i++)
// {
// cnt = sum = 0;
// for(int j = 1; j <= M; j++)
// {
// if(Map[i][j].h == -1)
// {
// addEdge(T+i, point(i, j), 8);
// cnt++;
// }
// else
// sum += Map[i][j].h;
// }
// if(cnt)
// addEdge(S, T+i, sum-cnt);
// }
// //对列处理
// for(int j = 1; j <= M; j++)
// {
// cnt = sum = 0;
// for(int i = 1; i <= N; i++)
// {
// if(Map[i][j].h == -1)
// {
// addEdge(point(i, j), T+N+j, 8);
// cnt++;
// }
// else
// sum += Map[i][j].v;
// }
// if(cnt)
// addEdge(T+N+j, T, sum-cnt);
// }
//}
int numx[110][110], numy[110][110];
int xval[MAXN], yval[MAXN];
int Xn, Yn;
void getMap()
{
Xn = Yn = 0;
init();
for(int i = 1; i <= N; i++)
{
for(int j = 1; j <= M; j++)
{
if(Map[i][j].h >= 0)
xval[++Xn] = Map[i][j].h;
else if(Map[i][j].h == -1)
{
xval[Xn]--;
numx[i][j] = Xn;
}
}
}
for(int j = 1; j <= M; j++)
{
for(int i = 1; i <= N; i++)
{
if(Map[i][j].v >= 0)
yval[++Yn] = Map[i][j].v;
else if(Map[i][j].v == -1)
{
yval[Yn]--;
numy[i][j] = Yn;
}
}
}
S = 0, T = Xn+Yn+1;
for(int i = 1; i <= Xn; i++) addEdge(S, i, xval[i]);
for(int i = 1; i <= Yn; i++) addEdge(Xn+i, T, yval[i]);
for(int i = 1; i <= N; i++)
for(int j = 1; j <= M; j++)
if(Map[i][j].h == -1)
addEdge(numx[i][j], numy[i][j]+Xn, 8);
}
bool BFS(int s, int t)
{
queue<int> Q;
memset(dist, -1, sizeof(dist));
memset(vis, false, sizeof(vis));
dist[s] = 0;
vis[s] = true;
Q.push(s);
while(!Q.empty())
{
int u = Q.front();
Q.pop();
for(int i = head[u]; i != -1; i = edge[i].next)
{
Edge E = edge[i];
if(!vis[E.to] && E.cap > E.flow)
{
dist[E.to] = dist[u] + 1;
if(E.to == t) return true;
vis[E.to] = true;
Q.push(E.to);
}
}
}
return false;
}
int DFS(int x, int a, int t)
{
if(x == t || a == 0) return a;
int flow = 0, f;
for(int &i = cur[x]; i != -1; i = edge[i].next)
{
Edge &E = edge[i];
if(dist[E.to] == dist[x] + 1 && (f = DFS(E.to, min(a, E.cap-E.flow), t)) > 0)
{
edge[i].flow += f;
edge[i^1].flow -= f;
flow += f;
a -= f;
if(a == 0) break;
}
}
return flow;
}
void Maxflow(int s, int t)
{
while(BFS(s, t))
{
memcpy(cur, head, sizeof(head));
DFS(s, INF, t);
}
}
int query(int u, int v)
{
for(int i = head[u]; i != -1; i = edge[i].next)
if(edge[i].to == v)
return edge[i].flow;
}
void solve()
{
Maxflow(S, T);
for(int i = 1; i <= N; i++)
{
for(int j = 1; j <= M; j++)
{
if(j > 1) printf(" ");
if(Map[i][j].h == -1)
printf("%d", query(numx[i][j], numy[i][j]+Xn)+1);
else
printf("_");
}
printf("\n");
}
}
int main()
{
while(scanf("%d%d", &N, &M) != EOF)
{
input();
getMap();
solve();
}
return 0;
}