查找总结

1.折半查找

        折半查找又称二分查找（Binary Search）过程是：先确定待查找记录所在区间，然后逐步缩小查找区域直到找到或找不到记录为止。折半查找适用于查找表有序，否则不能使用折半查找。

//在大小为len的有序数组arr中查找记录key
//找到返回1,找不到返回0
int BinarySearch(int *arr, int key, int len)
{
	//初始待查找区域[low..high]为[0..len - 1]
	int low = 0, high = len - 1, mid;
	while(low <= high)
	{
		mid = low + (high - low) / 2; //待查找区域中间元素,不使用(low + high) / 2来计算mid是防止溢出
		if(key > arr[mid])  //key在待查找区域中间元素右侧
		{
			low = mid + 1; //更新待查找区域[mid + 1..high]
		}
		else if(key < arr[mid]) //key在待查找区域中间元素左侧
		{
			high = mid - 1; //更新待查找区域[low..mid - 1]
		}
		else
		{
			return 1; //找到待查找元素返回1
		}
	}
	return 0; //未找到待查找元素返回0
}

折半查找时间复杂度为O（nlgn）。

2.二叉查找树

      查找树是一种数据结构，它支持多种动态集合操作，包括SEARCH，MINIMUM，MAXIMUM，PREDECESSOR，SUCCESSOR，INSERT以及DELETE。二叉查找树具有以下性质：

1）二叉查找树结点x的左子树的结点值都不大于结点x的值。

2）二叉查找树结点x的右子树的结点值都不小于结点x的值。

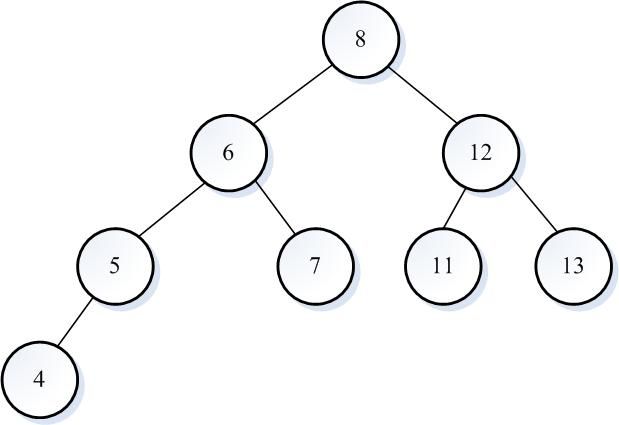
如图1所示为二叉查找树，根结点左子树所有结点值都小于根结点，右子树所有结点值都大于根结点。

 

2.1二叉查找树存储结构

struct BiSearchTree //二叉查找树结点结构
{
	int data; //结点数据
	BiSearchTree *left; //指向左子树
	BiSearchTree *right; //指向右子树
	BiSearchTree *parent; //指向父结点
	
	//结点初始化
	BiSearchTree(int data) : left(NULL), right(NULL), parent(NULL)
	{
		this->data = data;
	}
};

2.2建立二叉查找树

        将元素x插入二叉查找树中的过程：找到元素x在二叉查找树中的位置，修改树的某些域，并x插入树中。

// 建立二叉查找树
void MakeTree(BiSearchTree *&tree, int data)
{
	if(tree == NULL) //二叉树为空
	{
		tree = new BiSearchTree(data); //创建二叉查找树根结点
	}
	else
	{
		BiSearchTree *p = tree;
		BiSearchTree *q = tree;
		while(q != NULL) //查找元素data插入位置
		{
			p = q;
			(q->data > data) ? (q = q->left) : (q = q->right);
		}
		
		q = new BiSearchTree(data);
		q->parent = p;
		(p->data > data) ? (p->left = q) : (p->right = q);
	}
}

2.3在二叉查找树中查找指定记录key

        从根结点开始查找，对每个结点x，如果待查找记录等于当前结点即key=key[x]，找到待查找记录，查找结束；如果待查找记录小于当前结点即key<key[x]，则继续查找该结点的左子树；如果待查找记录大于当前结点即key>key[x]，则继续查找该结点的右子树。

// 在二叉查找树中查找关键字为key的结点(非递归算法)
BiSearchTree *find(BiSearchTree *tree, int key)
{
	if(tree == NULL)
		return NULL;

	BiSearchTree *p = tree;
	while(p != NULL)
	{
		if(p->data > key)
			p = p->left;
		else if(p->data < key)
			p = p->right;
		else 
			return p;
	}
	
	return NULL;
}

// 在二叉查找树中查找关键字为key结点的递归方法
BiSearchTree *find(BiSearchTree *tree, int key)
{
	if(tree == NULL)
		return NULL;
	if(tree != NULL && tree->data == key)
		return tree;
	if(tree->data > key)
		return find(tree->left, key);
	else
		return find(tree->right, key);
}

2.4MINIMUM操作

        因为二叉查找树的性质保证结点x的左子树都不大于它。因此查找二叉查找树关键字最小的结点，可以从根结点开始，沿着各结点的left指针查找下去，直到遇到NULL为止。

// 查找树中的最小关键字
BiSearchTree *TreeMinimum(BiSearchTree *tree)
{
	if(tree == NULL) //树为空返回NULL
		return NULL;


	BiSearchTree *min = tree;
	while(min->left != NULL)
	{
		min = min->left;
	}


	return min;
}

2.5MAXIMUM操作

        和MINIMUM操作类似，因为结点x的右子树都不小于它。因此查找二叉查找树关键字最大的结点，可以从根结点开始，沿着各结点的right指针查找下去，直到遇到NULL为止。

// 查找树中最大关键字
BiSearchTree *TreeMaximum(BiSearchTree *tree)
{
	if(tree == NULL) //树为空返回NULL
		return NULL;


	BiSearchTree *max = tree;
	while(max->right != NULL)
	{
		max = max->right;
	}
	return max;
}

2.6SUCCESSOR操作

        查找给定结点在中序遍历下的后继。如果所有关键字都不相同，则某一结点x的后继即具有大于key[x]中的关键字中最小者的那个结点。如果结点x的右子树非空，则x的后继即为右子树中最左结点(由中序遍历性质知)。如果结点x的右子树为空，且x有一个后继y，则y是x的最低祖先结点。

// 查找结点x的后继
BiSearchTree *TreeSuccessor(const BiSearchTree *x)
{
	if(x == NULL) // 结点不存在时返回NULL
	{
		return NULL;
	}
	if(x->right != NULL) // 结点的右子树不为空时返回该结点的右子树关键字最小的结点
	{
		return TreeMinumum(x->right);
	}

	// 当结点的右子树为空时
	// 该结点的后继为从该结点依次向上找直到遇到某个是其父结点的左儿子结点为止
	BiSearchTree *y = x->parent;
	while(y != NULL && x == y->right)
	{
		x = y;
		y = y->parent;
	}

	return y;
}

2.7PRECESSOR操作

        和SUCCESSOR操作对称。如果所有关键字都不相同，则某一结x的前趋即具有小于key[x]中的关键字中最大者的那个结点。如果如果结点x的左子树非空，则x的前赵即左子树中最右结点。如果结点x的左子树为空，且x有一个前趋y，则y是最低祖先结点。

// 查找结点x的前驱
BiSearchTree *TreePredecessor(BiSearchTree *x)
{
	if(x == NULL) // 结点不存在返回NULL
		return NULL;
	
	if(x->left != NULL) // 结点x的左子树不为空时返回左子树中关键字最大的结点
		return TreeMaximum(x->left);
	
	// 结点x的左子树为空
	// 该结点的前驱为从该结点依次向上查找直到遇到某个结点是其父结点的右儿子结点为止
	BiSearchTree *y = x->parent;
	while(y != NULL && x == y->left)
	{
		x = y;
		y = y->parent;
	}
	return y;
}

2.8中序遍历

        对二叉树进行中序遍历得到的是一系列有序的记录，因此对一组记录建立二叉查找树，再中序遍历，实际是对这组记录进行排序。

// 中序遍历二叉查找树
void TreeInOrder(BiSearchTree *tree)
{
	if(tree != NULL)
	{
		TreeInOrder(tree->left);
		cout << tree->data << endl;
		TreeInOrder(tree->right);
	}
}