Experimental Educational Round: VolBIT Formulas Blitz（数学、组合数学）

A Again Twenty Five!

题意:求5n的最后2位,2≤n≤1018
分析：直接 puts("25");

B Moore’s Law

题意:求n⋅1.000000011t
分析:ans=n∗pow(1.000000011,t)

C Lucky Numbers

题意:求最大位数是n的,只含7活8的数字个数
分析:ans=21+22+⋯+2n=2n+1−2

D Hexagons!

题意:求构成n层大正六边形的小正六边形个数
分析:看每个边发现每层多6个,然后就是等差数列
ans=1+6∗n+n∗(n−1)/2∗6

E A rectangle

题意:给定奇怪的坐标系,求矩形(x1≤x2,y1≤y2)内六边形的中心个数,保证(x1,y1)是六边形中心,且(x2−x1)%2==0

分析:限定条件后,发现纵轴六边形个数是n,n−1交替
直接当n算,减去多的一半个数
ans=((y2−y1)/2+1)∗(x2−x1+1)−(x2−x1)/2;

F Selection of Personnel

题意:从n个人选一组5、6或7个人的方法数
分析:ans=C5n+C6n+C7n

G Challenge Pennants

题意:n个不同的桌子,A物品5个,B物品3个,A,B物品必须都放置,求方法数
分析:就是允许有空的嘛,各加上n个物品转化成隔板法,然后乘法原理乘起来
ans=Cn−15+n−1∗Cn−13+n−1

H Benches

题意:5个不同的棋子放在n×n的网格交点上,求方法数
分析:x与y坐标选取独立,各自方法数是C5n,选好以后由于不同再全排列
ans=(C5n)2∗P55

I Parking Lot

题意:2∗n−2个停车位,4种类型的车,要求必须有一种车连续n个,求方法数
分析:我不会组合数学解法,考虑dp,f[i][0/1]:=前i个车,是否有连续n个同类型车,的方法数
f[i][0]=1,f[i][0]=0,暴力转移,特判开头的车4种方法数,之后的3种

f[0][0] = 1;
for(int i = 1; i <= 2 * n - 2; ++i) {
    if(i >= n) f[i][1] += (i == n ? 4 : 3) * f[i - n][0];
    for(int j = 1; j <= i && j <= n; ++j) {
        f[i][0] += (i == j ? 4 : 3) * f[i - j][0];
        f[i][1] += (i == j ? 4 : 3) * f[i - j][1];
    }
}

ans=f[2∗n−2][1]

J Divisibility

题意:求[1,n]同时被numbers∈[2,10]整除的数的个数
分析:ans=n/lcm10i=2i=n/2520

K Indivisibility

题意:求[1,n]不被numbers∈[2,10]整除的数的个数
分析:ans=n−E[1,n]被numbers∈[2,10]整除的数
后面这个容斥原理就好了,容斥一下lcm

vector<int> v;
for(int i = 2; i <= 10; ++i) v.push_back(i);
long long ans = n;
for(int i = 1; i < 1 << 9; ++i) {
    int cnt = 0, lcm = 1;
    for(int j = 0; j < 9; ++j)
        if(i >> j & 1) lcm = lcm / __gcd(lcm, v[j]) * v[j], ++cnt;
    if(cnt & 1) ans -= n / lcm;
    else ans += n / lcm;
}
printf("%I64d\n", ans);

L Cracking the Code

题意:给定一个重排数字方式,N→Nc,求N5c的后5位数
分析：直接模拟

char s[10], t[10];
int d[] = {0, 1, 3, 5, 4, 2};
for(int i = 1; i <= 5; ++i) t[i] = s[d[i]];
long long x = atoi(t + 1), ans = 1;
for(int i = 1; i <= 5; ++i)
    ans = ans * x % 100000;
printf("%05I64d\n", ans);

M Turn

题意:照图的意思(蓝儿题里相反)就是,+度数代表逆时针转的,−度数代表顺时针转的,问需要顺时针转几下才能和0∘差距最小
分析:暴力枚举0∼3次旋转,取最小那个

int dif = INF, ans = -1;
for(int i = 0; i < 4; ++i) {
    int y = ((x - 90 * i) % 360 + 360) % 360;
    y = min(y, 360 - y);
    if(y < dif) ans = i, dif = y;
}
printf("%d\n", ans);

N Forecast

题意:给定必有2个实根的二元一次方程,输出两个根
分析：求根公式

double delta = sqrt(b * b - 4 * a * c);
double r1 = (-b - delta) / 2 / a, r2 = (-b + delta) / 2 / a;
if(r1 < r2) swap(r1, r2);
printf("%.12f\n%.12f\n", r1, r2);

O Arrow

题意:给定图上的那些东西,然后求向量指向的端点,逆时针输出
分析：计算几何模版直接搞

double px, py, vx, vy, a, b, c, d;

struct Point {
    double x, y;
    void read() {scanf("%lf%lf", &x, &y);}
    void print() {printf("%.12f %.12f\n", x, y);}

    Point operator+(const Point& p) {
        return {x + p.x, y + p.y};
    }
    Point operator-(const Point& p) {
        return {x - p.x, y - p.y};
    }
    Point operator*(const double& c) {
        return {c * x, c * y};
    }
    double length() {return hypot(x, y);}
    void normalize() {
        double len = length();
        x /= len;
        y /= len;
    }
    Point rotate() { //clock-wise;
        return {y, -x};
    }
};

using Vector = Point;

cin >> px >> py >> vx >> vy >> a >> b >> c >> d;

Point p = {px, py};
Vector v = {vx, vy};
v.normalize();
Vector w = v.rotate();

(p + v * b).print();
(p - w * (a / 2.)).print();
(p - w * (c / 2.)).print();
(p - w * (c / 2.) - v * d).print();
(p + w * (c / 2.) - v * d).print();
(p + w * (c / 2.)).print();
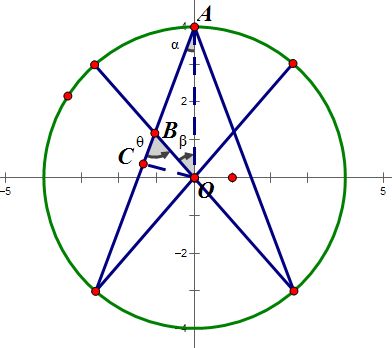
(p + w * (a / 2.)).print();

P Area of a Star

题意:给定n,r,求圆内接正n角星的面积
分析:就是求图中的这个三角形面积,作OC垂直于AB交于C,三角函数搞一搞
S=2n∗S△OAB

double alpha = PI / n / 2, beta = PI / n;
double theta = alpha + beta;
double OC = r * sin(alpha), OB = OC / sin(theta);
double ans = n * OB * r * sin(beta);
printf("%.12f\n", ans);

Q Pyramids

题意:求所有边长相等的正n棱锥的体积
分析:以这样的正三棱锥举例:

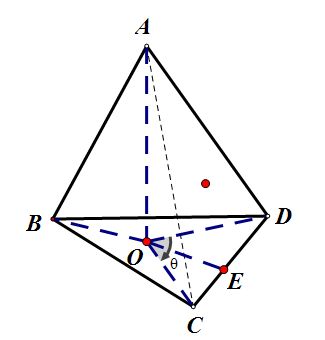
首先θ=2π/n
作OE垂直于CD于E,在S△OCE中,OC=12lsin(12θ)
作AO垂直于S△BCD于O,在S△AOC中,AO=l2−|OC|2−−−−−−−−−√
S△BCD=n⋅S△OCD=n⋅12|OC|2⋅sin(θ)
S=13⋅|AO|⋅S△BCD
问题解决

int l[10];
double base, height;

void get(int n) {
    double theta = 2 * acos(-1) / n;
    double OC = 0.5 * l[n] / sin(theta / 2);
    base = n * (0.5 * OC * OC * sin(theta));
    height = sqrt(l[n] * l[n] - OC * OC);
}

for(int i = 3; i <= 5; ++i) scanf("%d", l + i);
double ans = 0;
for(int i = 3; i <= 5; ++i) {
    get(i);
    ans += base * height / 3;
}
printf("%.12f\n", ans);

R Game

题意:给定n×n的网格,游戏规则如下:两个轮流选格子,但是选取的格子不能与任意一个格子共边,不能选取者输
假设两人均采取最优策略,先手赢输出1,后手输出2
分析:画1×1,2×2,3×3,4×4,5×5的发现,n为奇数时多种方法选取中能选取的格子总是奇数个,n为偶数有偶数个
故n为奇数先手赢,偶数后手赢
直接 puts(n & 1 ? "1" : "2");