平衡二叉树实现-旋转
来源http://www.cnblogs.com/Clingingboy/archive/2010/10/08/1845854.html
继续讨论旋转
为了方便讨论是做点记号
- X为插入的节点
- P为旋转轴(P有时候为X的父节点如LL,RR旋转;P有时候也为X,如LR,RL旋转)
- R为平衡因子绝对值=2的节点
看下面四种情况
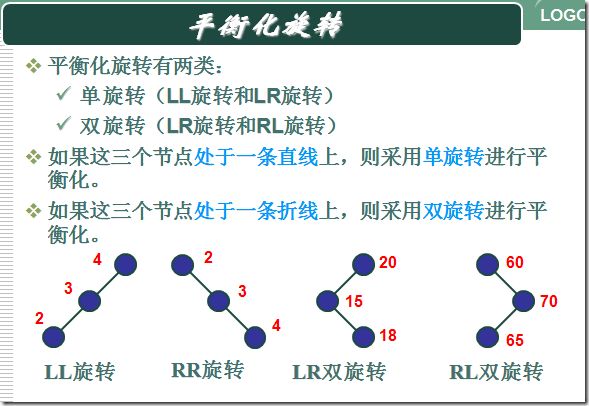
LL旋转
当三个节点处于一条直线,并均是左节点时,需要以中间的节点为旋转轴向右侧(顺时针)旋转一次
- 使得C成为B的右子节点
- B代替C的位置
- B的右子节点成为C的左子节点
private Node LL(Node root) { Node rootNext = root.Left; root.Left = rootNext.Right; rootNext.Right = root; return rootNext; }
RR旋转
当三个节点处于一条直线,并均是左节点时,需要以中间的节点为旋转轴向左侧(逆时针)旋转一次
- 使得A成为B的左子节点
- B代替A的位置
- B的左子节点成为A的右子节点
private Node RR(Node root) { Node rootNext = root.Right; root.Right = rootNext.Left; rootNext.Left = root; return rootNext; }
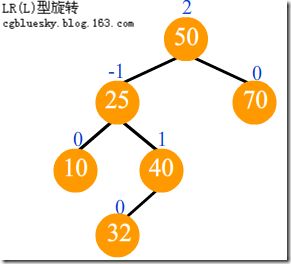
LR旋转
P为R的左节点,X为P右节点
当三个节点不处于一条直线,并均是左节点时,需要以插入的节点为旋转轴向左侧(逆时针)旋转一次,然后向右侧(顺时针)旋转一次,即先做RR旋转再做一次LL旋转
执行RR旋转(参照RR旋转规则)
- 使得A成为B的左子节点
- B代替A的位置
- B的左子节点成为A的右子节点
注意现在是以B为旋转轴,所以C位置没有发生变化
现在可以执行LL旋转了(注意现在是以B为旋转轴了),同LL旋转一样
看图片左边部分
执行LL旋转
那么LR的代码如果借助LL和RR的方法则变得非常简单
private Node LR(Node root) root.Left = RR(root.Left); return LL(root); }
RL旋转
跟LR相关执行LL,RR旋转
private Node RL(Node root) { root.Right = LL(root.Right); return RR(root); }
LL,RR旋转后改变平衡因子
现实中旋转后我们马上可以得出平衡因子发生了变化,但在程序中我们必须手动对平衡因子做出改动
比如LL旋转前
- RH(R的平衡因子)=2
- PH=1
- X=0
旋转后
- RH=0
- PH=0
- X=0
LL
即当P的平衡因子为1时
if (rootNext.BF == 1)
{
root.BF = 0;
rootNext.BF = 0;
}
RR
即当P的平衡因子为-1时
if (rootNext.BF == -1)
{
root.BF = 0;
rootNext.BF = 0;
}
双旋转的合并
比如LR旋转
将LL和RR的代码合并在一起
private Node LR(Node root) { Node rootLeft = root.Left; //RR(rootLeft); Node pRight = rootLeft.Right; rootLeft.Right = pRight.Left; pRight.Left = rootLeft; root.Left = pRight; //LL(root); rootLeft = root.Left; root.Left = rootLeft.Right; rootLeft.Right = root; }
上面的代码让人看起来思路非常的清晰,但由于是程序,所以可以简化
rootLeft就是pRight
root.Left不要赋值两次
以下是改进
private Node LR(Node root) { Node rootLeft = root.Left; //RR(rootLeft); Node pRight = rootLeft.Right; rootLeft.Right = pRight.Left; pRight.Left = rootLeft; //LL root.Left = pRight.Right; pRight.Right = root; }
LR旋转后的平衡因子
有三种情景
1.P的平衡因子为0
R的平衡因子变为0,P的父节点平衡因子变为0,自身平衡因子变为0
2.P的平衡因子为-1
R的平衡因子变为-1,P的父节点平衡因子变为0,自身平衡因子变为0
3.P的平衡因子为1
R的平衡因子变为0,P的父节点平衡因子变为1,自身平衡因子变为0
switch (pRight.BF) { case 0: root.BF = 0; rootLeft.BF = 0; break; case 1: root.BF = -1; rootLeft.BF = 0; break; case -1: root.BF = 0; rootLeft.BF = 1; break; } pRight.BF = 0;
旋转的选择
当R的绝对值等于2时,如果等于2说明树的左边加入了一个节点,反之则是右侧节点.
当R==2时,则检查R的左侧节点的平衡因子,有两种情况1或-1,如果是1的话,则LL旋转,如果是-1的话则LR旋转
反之当R==-2时,情况则刚好相反
private bool RotateSubTree(int bf) { Node root = path[currentIndex], newRoot = null; if (bf == 2) { int leftBF = root.Left.BF; if (leftBF == -1) { newRoot = LR(root); } else if (leftBF == 1) { newRoot = LL(root); } } if (bf == -2) { int rightBF = root.Right.BF; if (rightBF == 1) { newRoot = RL(root); } else if (rightBF == -1) { newRoot = RR(root); } } }话题全是紧扣着旋转和平衡因子,还未完...