数据结构笔记3 线性表的链式表示

线性链表的相关概念：

线性表的链式表示是用一组任意的存储单元存储线性表的数据元素（这组存储单元可以是连续的，也可以是不连续的）。
表示每个数据元素的两部分（数据、后继元素存储地址）信息组合在一起被称为结点；
它包括两个域：
      其中表示数据元素内容的部分被称为数据域（data）；
      表示直接后继元素存储地址的部分被称为指针域（next），
      指针域中存储的信息称为指针或链。
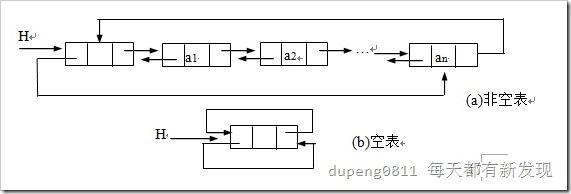
 N个结点（ai（1≤i≤n）的存储映射）链结成一个链表，即为线性表(a1，a2，… ai-1，ai，ai+1，…an)的链式存储结构（非顺序映射）。
      头指针指示链表中结点的存储地址。

 

链式存储结构的特点：

插入、删除操作是不再需要移动大量的元素，但失去了顺序表的可随机存取特点。
它是非随机存取结构。
链表可分为单链表、循环链表和双向链表。

 

 

线性链表

链表中的每一个结点中只包含一个指针域的称为单链表或线性链表。
 
  
  
  
  

   
   
   
   
访问操作：
  
  
  
  
单链表是非随机存取结构。每个元素的位置信息都包含在前驱结点的信息中，
所以取得第i个元素必须从头指针出发寻找。设置一个指针变量指向第一个结点，
然后，让该指针变量逐一向后指向，直到第i个元素。假设p是指向线性表中第I个数据元素（结点ai）的指针，
则p→next是指向第I+1个数据元素（结点ai+1）的指针，或若p→data=ai，则p→next→data= ai+1。
  
  
  
  

   
   
   
   
插入操作：
  
  
  
  
要在数据元素a和b 之间插入元素x。
算法思想：决定a和b之间的相邻关系是由a 的指针决定的。若要实现插入，生成x结点，然后让a 的指针指向x 且x 的指针指向b。实现三个元a、x和b的逻辑关系。
设p为指向结点a 的指针，s为指向结点x的指针，则修改s、a的指针：
s→next=p→next；p→next=s；
 
  
  
  
  

   
   
   
   
删除操作：
  
  
  
  
在单链表数据元素a、b、c三个相邻的元素中删除b，算法思想：就是要让a 的指针直接指向c，使b从链表中脱离。
即，p→next=p→next→next。
可见，在已知链表中元素插入或删除的确切位置的情况下，在单链表中插入或删除一个结点时，紧需修改指针而不需要移动元素。
 

循环链表

循环链表：是另一种形式的链式存储结构，其特点是表中最后一个结点的指针域指向头结点，整个链表形成一个环。
循环链表可分为单链和多链的。
循环链表的操作：和线性链表基本一致，差别仅在于循环条件判定是否为空改为是否为头指针,即：p或p->next=s。

双向链表

双向链表：在双向链表的结点中有两个指针域，分别指向前驱和后继。
双向链表也可以有循环链表。
 
  
  
  
  

   
   
   
   
双向链表的操作：
  
  
  
  
若d为指向表中某一接点的指针（即d为DuLinkList 型变量），则显然有d->next->prior=d->prior->next=d
双指针使得链表的双向查找更为方便、快捷。NextElem和PriorElem的执行时间为O（1）。
仅需涉及一个方向的指针的操作和线性链表的操作相同。
插入和删除需同时修改两个方向的指针。

 

顺序表和链表的比较

在本章介绍了线性表的逻辑结构及它的两种存储结构：顺序表和链表。通过对它们的讨论可知它们各有优缺点，顺序存储有三个优点：

(1) 方法简单，各种高级语言中都有数组，容易实现。

(2) 不用为表示结点间的逻辑关系而增加额外的存储开销。

(3) 顺序表具有按元素序号随机访问的特点。

但它也有两个缺点：

(1) 在顺序表中做插入删除操作时，平均移动大约表中一半的元素，因此对n较大的顺序表效率低。

(2) 需要预先分配足够大的存储空间，估计过大，可能会导致顺序表后部大量闲置；预先分配过小，又会造成溢出。

链表的优缺点恰好与顺序表相反。在实际中怎样选取存储结构呢？通常有以下几点考虑：

１．基于存储的考虑

顺序表的存储空间是静态分配的，在程序执行之前必须明确规定它的存储规模，也就是说事先对＂MAXSIZE＂要有合适的设定，过大造成浪费，过小造成溢出。
可见对线性表的长度或存储规模难以估计时，不宜采用顺序表；链表不用事先估计存储规模，但链表的存储密度较低，
存储密度是指一个结点中数据元素所占的存储单元和整个结点所占的存储单元之比。显然链式存储结构的存储密度是小于１的。

２．基于运算的考虑

在顺序表中按序号访问ai的时间性能时O(1)，而链表中按序号访问的时间性能O(n)，所以如果经常做的运算是按序号访问数据元素，显然顺序表优于链表；
而在顺序表中做插入、删除时平均移动表中一半的元素，当数据元素的信息量较大且表较长时，这一点是不应忽视的；
在链表中作插入、删除，虽然也要找插入位置，但操作主要是比较操作，从这个角度考虑显然后者优于前者。

３．基于环境的考虑

顺序表容易实现，任何高级语言中都有数组类型，链表的操作是基于指针的，相对来讲前者简单些，也是用户考虑的一个因素。

总之，两中存储结构各有长短，选择那一种由实际问题中的主要因素决定。通常“较稳定”的线性表选择顺序存储，
而频繁做插入删除的即动态性较强的线性表宜选择链式存储。