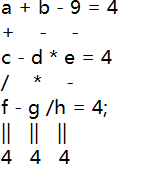2015腾讯在线笔试的一道编程题
摘要:昨天刚刚看了一道同学的腾讯在线笔试编程题;大致如下:
要求求出未知数在1到100以内所有的可能组合,(横着第三行的等式记不清楚了,自己随便添加的符号)
基本思路(1)以前没有专门刷过题,第一次遇到这种题目,首先思考了一下常用的几个算法,发现几乎都不合适,因为这道题不是求解最优化的问题,也不容易划分成问题不相干的子集求解.唯一感觉有点可能的是回溯算法,因为涉及穷举所有的可能.
(2)因此思考了一下暴力求解的可能,直接进行穷举.发现这里的计算与回溯思路基本相同,都是先做出一个决策(确定某个等式上的未知数值),然后递归的计算下一个等式的未知数.注意到前三个横着的等式可以确定所有可能的未知数,而三个竖着的等式则是用来判断这个些未知数到底符不符合所有的等式要求.
(3)思考到这里基本框架就出来了,传入一个变量Index用来确定到底是计算哪一个等式,同时判定是计算未知数还是验证等式.当最后一个等式通过时就输出所有未知数.
(4)然后需要思考的编程细节上的一些东西,这也是做题时最花时间的东西,
【1】首先要构建一个函数用来判断是否满足本次调用时应该满足的等式,如果满足就计算下一个,如果不满足就要重新计算新的未知数.
【2】然后要注意每个等式和未知变量(定义为一个全局数组A【10】,A[0]不用)之间的关系,比如前三个等式的编号是1,2,3(index),那么每次确定的变量是A[3*index -2],A[3*index -1],A[3*index ].计算后三个等式时要将数组A【10】里面的元素传入验证函数,这时候index(4,5,6)与A【10】的关系是传入A[index - 3],A[index],A[index +3]
【3】做到这里程序就可以运行了,但是还存在一些问题,首先第一个等式是比较特殊的,它的一个未知数是确定的9.但是由于函数递归调用要考虑所有等式的情况,所以还是得写一个3重循环来进行遍历3个未知数.为了提高效率,我们可以在index == 1的时候进行一次跳转,给未知数c直接赋值,同时注意到等式变为a+b == 4+9 =13,那么其实只需要一重循环就可以了.这样可以避免重复的计算.
【4】但是运行之后可以发现这样的计算还是效率太低,计算机不足以在规定时间之内算出所有的解,提高效率是必须的.其实从等式1可以发现,含有三个未知数的等式只需要两重循环就可以得到所有符合该等式的解,但是难点就是每一个等式都不一样,写出一个通用的框架很麻烦.当然为了节约时间可以先进行一些显而易见的提升.
【5】凭借小学数学知识就知道很多未知数是存在一个范围的,比如第一个等式中的a+ b = 13,a,b不可能大于12,这样就只需要1到12的一次循环就可以了,同时第4个等式有a+c/f == 4,那么a就不会超过3,这样a的范围就成了1到3.同理可以确定其他很多变量的范围,而这些工作通过人为的分析可以提前完成,作为全局变量存储.(要将所有变量的范围计算精确可能不一定容易但是迅速的缩小到一个大概的范围是不困难的)
如图: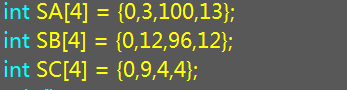
代表了范围的最大值,最小值,没有计算.比如第一个等式的a ≤ SA[1]。第index个等式的b ≤ SB[index]。
【6】通过这些修改程序可以很快的得出结果了,至于更麻烦的提高效率(循j减少环次数)更新在最后,毕竟这是一道笔试题,时间才是重要的.写出这道程序大概花了2个多小时,因为第一次遇见这类题目,花了比较多的时间去思考和修改.但是如果再次碰见应该可以很快的做出来了,
#include "stdafx.h"
int A[10] = {0};
int SA[4] = {0,3,100,13};
int SB[4] = {0,12,96,12};
int SC[4] = {0,9,4,4};
#define N 100
int Issatisfited(int a,int b,int c,int index)
{
switch(index)
{
case 1:
return (a+b) == 13;
break;
case 2:
return (a-b*c) == 4;
break;
case 3:
return a+b*c == 14;
break;
case 4:
return (a+b/c) == 4&&(b%c==0);
break;
case 5:
return (a - b*c) == 4;
break;
case 6:
return (a - b - c) == 4;
break;
}
}
void Print()
{
int i = 1;
while(i<=9)
{
printf("%d ",A[i++]);
}
puts("\n");
}
void test(int index)
{
int k,a,b,c;
if (index <=3)
{
for(a = 1;a<=SA[index];a++)//计算所有可能的未知数.
{
if(index == 1)
{
b = 13 - a;
c = 9;
goto Test;
}
for(b = 1;b<=SB[index];b++)
{
for(c = 1;c<=SC[index];c++)
{
Test:if(Issatisfited(a,b,c,index))
{
k = 3*index - 2;
A[k] = a;
A[k+1] = b;
A[k+2] = c;
test(index+1);
}
}
}
}
}
else//检验所有的结果
{
for(k = 1;k<=3;k++)
{
a = A[k] ;
b = A[k+3];
c = A[k+6] ;
if(Issatisfited(a,b,c,k+3))
{
if(k == 3)
Print();
}
else
return;
}
}
}
int _tmain(int argc, _TCHAR* argv[])
{
test(1);
return 0;
}
=====================================
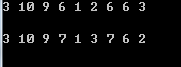
结果
更新::最多用到两层循环.但是用了很多goto(这里所有的goto都是向下进行的,减少出错的可能,千万不能往上走,很容易出错),不是很好,而且使得程序的可读性下降了很多.
void test(int index)
{
int k,a,b,c;
if (index <=3)
{
for(a = 1;a<=SA[index];a++)
{
if(index == 1)
{
b = 13 - a;
c = 9;
goto Test;
}
for(b = 1;b<=SB[index];b++)
{
if (index == 2)//计算第二个等式
{
if(a>4&&(a-4)%b==0)
{
c = (a-4)/b;
goto Test;
}
else
continue;
}
else if (index == 3)
{
if(a>4&&b%(a-4)==0)
{
c = b/(a-4);
goto Test;
}
else
continue;
}
Test:if(Issatisfited(a,b,c,index))
{
k = 3*index - 2;
A[k] = a;
A[k+1] = b;
A[k+2] = c;
test(index+1);
}
}
}