Given a string S, find the longest palindromic substring in S.
Note:
This is Part II of the article: Longest Palindromic Substring. Here, we describe an algorithm (Manacher’s algorithm) which finds the longest palindromic substring in linear time. Please read Part I for more background information.
In my previous post we discussed a total of four different methods, among them there’s a pretty simple algorithm with O(N2) run time and constant space complexity. Here, we discuss an algorithm that runs in O(N) time and O(N) space, also known as Manacher’s algorithm.
Hint:
Think how you would improve over the simpler O(N2) approach. Consider the worst case scenarios. The worst case scenarios are the inputs with multiple palindromes overlapping each other. For example, the inputs: “aaaaaaaaa” and “cabcbabcbabcba”. In fact, we could take advantage of the palindrome’s symmetric property and avoid some of the unnecessary computations.
An O(N) Solution (Manacher’s Algorithm):
First, we transform the input string, S, to another string T by inserting a special character ‘#’ in between letters. The reason for doing so will be immediately clear to you soon.
For example: S = “abaaba”, T = “#a#b#a#a#b#a#”.
To find the longest palindromic substring, we need to expand around each Ti such that Ti-d … Ti+d forms a palindrome. You should immediately see that d is the length of the palindrome itself centered at Ti.
We store intermediate result in an array P, where P[ i ] equals to the length of the palindrome centers at Ti. The longest palindromic substring would then be the maximum element in P.
Using the above example, we populate P as below (from left to right):
T = # a # b # a # a # b # a # P = 0 1 0 3 0 1 6 1 0 3 0 1 0
Looking at P, we immediately see that the longest palindrome is “abaaba”, as indicated by P6 = 6.
Did you notice by inserting special characters (#) in between letters, both palindromes of odd and even lengths are handled graciously? (Please note: This is to demonstrate the idea more easily and is not necessarily needed to code the algorithm.)
Now, imagine that you draw an imaginary vertical line at the center of the palindrome “abaaba”. Did you notice the numbers in P are symmetric around this center? That’s not only it, try another palindrome “aba”, the numbers also reflect similar symmetric property. Is this a coincidence? The answer is yes and no. This is only true subjected to a condition, but anyway, we have great progress, since we can eliminate recomputing part of P[ i ]‘s.
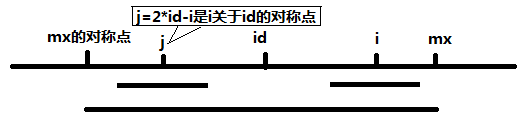
Let us move on to a slightly more sophisticated example with more some overlapping palindromes, where S = “babcbabcbaccba”.
Above image shows T transformed from S = “babcbabcbaccba”. Assumed that you reached a state where table P is partially completed. The solid vertical line indicates the center (C) of the palindrome “abcbabcba”. The two dotted vertical line indicate its left (L) and right (R) edges respectively. You are at index i and its mirrored index around C is i’. How would you calculate P[ i ] efficiently?
Assume that we have arrived at index i = 13, and we need to calculate P[ 13 ] (indicated by the question mark ?). We first look at its mirrored index i’ around the palindrome’s center C, which is index i’ = 9.
The two green solid lines above indicate the covered region by the two palindromes centered at i and i’. We look at the mirrored index of i around C, which is index i’. P[ i' ] = P[ 9 ] = 1. It is clear that P[ i ] must also be 1, due to the symmetric property of a palindrome around its center.
As you can see above, it is very obvious that P[ i ] = P[ i' ] = 1, which must be true due to the symmetric property around a palindrome’s center. In fact, all three elements after C follow the symmetric property (that is, P[ 12 ] = P[ 10 ] = 0, P[ 13 ] = P[ 9 ] = 1, P[ 14 ] = P[ 8 ] = 0).
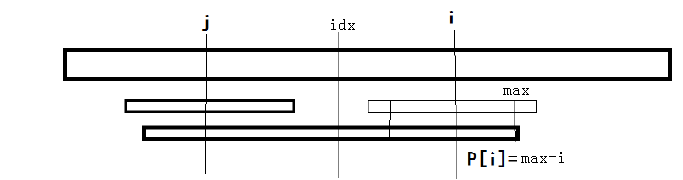
Now we are at index i = 15, and its mirrored index around C is i’ = 7. Is P[ 15 ] = P[ 7 ] = 7?
Now we are at index i = 15. What’s the value of P[ i ] ? If we follow the symmetric property, the value of P[ i ] should be the same as P[ i' ] = 7. But this is wrong. If we expand around the center at T15, it forms the palindrome “a#b#c#b#a”, which is actually shorter than what is indicated by its symmetric counterpart. Why?
Colored lines are overlaid around the center at index i and i’. Solid green lines show the region that must match for both sides due to symmetric property around C. Solid red lines show the region that might not match for both sides. Dotted green lines show the region that crosses over the center.
It is clear that the two substrings in the region indicated by the two solid green lines must match exactly. Areas across the center (indicated by dotted green lines) must also be symmetric. Notice carefully that P[ i ' ] is 7 and it expands all the way across the left edge (L) of the palindrome (indicated by the solid red lines), which does not fall under the symmetric property of the palindrome anymore. All we know is P[ i ] ≥ 5, and to find the real value of P[ i ] we have to do character matching by expanding past the right edge (R). In this case, since P[ 21 ] ≠ P[ 1 ], we conclude that P[ i ] = 5.
Let’s summarize the key part of this algorithm as below:
then P[ i ] ← P[ i' ]
else P[ i ] ≥ P[ i' ]. (Which we have to expand past the right edge (R) to find P[ i ].
See how elegant it is? If you are able to grasp the above summary fully, you already obtained the essence of this algorithm, which is also the hardest part.
The final part is to determine when should we move the position of C together with R to the right, which is easy:
In each step, there are two possibilities. If P[ i ] ≤ R – i, we set P[ i ] to P[ i' ] which takes exactly one step. Otherwise we attempt to change the palindrome’s center to i by expanding it starting at the right edge, R. Extending R (the inner while loop) takes at most a total of N steps, and positioning and testing each centers take a total of N steps too. Therefore, this algorithm guarantees to finish in at most 2*N steps, giving a linear time solution.
Note:
This algorithm is definitely non-trivial and you won’t be expected to come up with such algorithm during an interview setting. However, I do hope that you enjoy reading this article and hopefully it helps you in understanding this interesting algorithm. You deserve a pat if you have gone this far!
Further Thoughts:
- In fact, there exists a sixth solution to this problem — Using suffix trees. However, it is not as efficient as this one (run time O(N log N) and more overhead for building suffix trees) and is more complicated to implement. If you are interested, read Wikipedia’s article about Longest Palindromic Substring.
- What if you are required to find the longest palindromic subsequence? (Do you know the difference between substring and subsequence?)
Useful Links:
» Manacher’s Algorithm O(N) 时间求字符串的最长回文子串 (Best explanation if you can read Chinese)
» A simple linear time algorithm for finding longest palindrome sub-string
» Finding Palindromes
» Finding the Longest Palindromic Substring in Linear Time
» Wikipedia: Longest Palindromic Substring