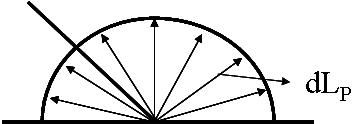
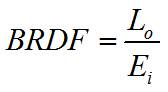双向反射率BRDF介绍
物体表面对电磁波的反射有三种形式:
" 镜面反射(mirror reflection)
反射能量集中在一个方向,反射角=入射角
" 漫反射(diffuse reflection)
整个表面都均匀地向各向反射入射光称为漫反射
" 方向反射(directional reflection)
介于漫反射和镜面反射之间,各向都有反射,
但各向反射强度不均一。
实际上多数自然表面对辐射的波长而言都是粗糙表面。当目标物的表面足够粗糙,以致于它对太阳短波辐射的反射辐射亮度在以目标物的中心的2π空间中呈常数,即反射辐射亮度不随观测角度而变,我们称该物体为漫反射体,亦称朗伯体。漫反射又 称朗伯(Lambert)反射,也 称各向同性反射。
介于漫反射和镜面反射之间反射称为方向反射,也称非朗伯反射。产生方向反射的物体在自然界中占绝大多数,即它们对太阳短波辐射的散射具有各向异性性质。当 遥感应用进入定量分析阶段,我们必须抛弃“目标是朗伯体”的假设。
目前大部分应用还都采用朗伯近似。
描述方向反射不能简单用反射率表述,因为各方向的反射率都不一样。
对非朗伯体而言,它对太阳短波辐射的反射、散射能力不仅随波长而变,同时亦随空间方向而变。
所谓地物的波谱特征是指该地物对太阳辐射的反射、散射能力随波长而变的规律。地物波谱特征与地物的组成成份,物体内部的结构关系密切,通俗讲地物波谱特征 也就是地物的颜色特征。
而地物的方向特征是用来描述地物对太阳辐射反射、散射能力在方向空间变化的,这种空间变化特征主要决定于两种因素,其一是物体的表面粗糙度,它不仅取决于 表面平均粗糙高度值与电磁波波长之间的比例关系,而且还与视角关系密切。
设波长为λ,空间具有δ分布函数的入射辐射,从 (θ0,φ0) 方向,以辐射亮度L0 (θ0,φ0,λ)投射向点目标,造成该点目 标的辐照度增量为dE (θ0,φ0,λ) = L0 (θ0,φ0,λ) cosθ0 dΩ。传感器从方向(θ,φ)观察目标物,接收到来自目标物对外来辐射dE的反射辐射,其亮度值为dL (θ,φ,λ)。
则定义双向反射率分布函数 :
XXX
![]()
f=dL/dE
双向反射率分布函数(BRDF)的物理意义是:来自方向地表辐照度的微增量与其所引起的方向上反射辐射亮度增量之间的比值。
这样定义的BRDF为什么可以恰当地表达地物的非朗伯体特性呢?
众所周知,在现实世界中投射到地物表面上的辐射能量往往有两部份组成,即来自太阳的直射辐射与天空散射辐射,而传感器在方向上测得的辐射亮度是空间入射辐射场的综合效应,它不仅与该点地物的反射特性有关,而且与辐射环境(即入射辐射亮度的空间分布函数)有关。
为了摆脱辐射环境的影响,我们采取两个措施:其一,设定入射辐射场为δ分布函数,其二,采用比值形式。
这样定义的 f 有如下三个特点:
" 与辐射环境无关,它仅与该地物的反射辐射特性有关,并且具有的 (Sr)-1 因次。
" 它是θ0,φ0, θ,φ,λ 五个自变量的函数,在2π空间中无论是入射还是反射均有无穷多个方向。(从概念上说要完整地表达一个物体的非朗伯体特性需要有无穷多个测量数据,而且这组无穷多个测量数据仅与一个具体对象相联系,例如对某一棵树的BRDF测量结果一般不同于对另一棵树的测量结果。实际上它使得对物体的非朗伯体的描述几乎成为不可能。所以重要的问题是能否对一类地物建立一种模型,从无穷多个测量数据集中找到一组个数有限的子集,它足以表征这类地物共同的对入射辐射的反射、散射特性,并且它与这类地物的空间结构特征有着稳定的函数关系,我们把这样的特殊子集称之为这类地物的方向谱。 )
" 这样定义的BRDF,虽然从理论上能较好地表征地物的非朗伯体特性,但在实际测量上困难较大,精确测量dE (θ0,φ0,λ)很困难。
双向反射率因子(Bi-directional Reflectance Factor, BRF)
定义:在相同的辐照度条件下,地物向(θ,φ)方向的反射辐射亮度与一个理想的漫反射体在该方向上的反射辐射亮度之比值,称为双向反射率因子R: