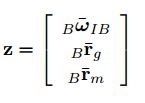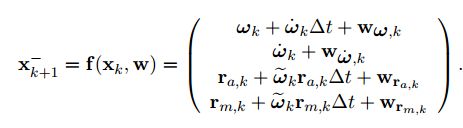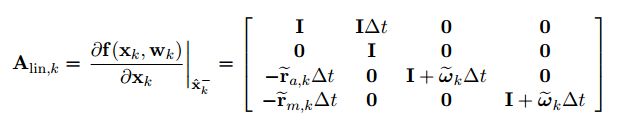PX4飞控中利用EKF估计姿态角代码详解



PX4飞控中利用EKF估计姿态角代码详解

http://blog.csdn.net/lizilpl/article/details/45542907

PX4飞控中主要用EKF算法来估计飞行器三轴姿态角，具体c文件在px4\Firmware\src\modules\attitude_estimator_ekf\codegen\目录下

• 具体原理
• 程序详解
• 下一步

1.具体原理

EKF算法原理不再多讲，具体可参见上一篇blog http://blog.csdn.net/lizilpl/article/details/45289541.

这篇讲EKF算法执行过程，需要以下几个关键式子：

• 飞行器状态矩阵：

  这里表示三轴角速度，

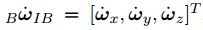  表示三轴角加速度，

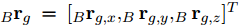  表示加速度在机体坐标系三轴分量，

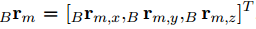  ，表示磁力计在机体坐标系三轴分量。

• 测量矩阵
  分别由三轴陀螺仪，加速度计，磁力计测得。

• 状态转移矩阵：

  飞行器下一时刻状态预测矩阵如下：

  

  其中W项均为高斯噪声， 为飞行器在姿态发生变化后，坐标系余旋变换矩阵，对该函数在处求一阶偏导，可得到状态转移矩阵：

  此时可得到飞行器状态的先验估计：

• 利用测量值修正先验估计：

  

  这里测量矩阵H与状态矩阵X为线性关系，故无需求偏导。

  卡尔曼增益：

  状态后验估计：

  方差后验估计：

2.程序详解

整个EKF的代码挺长的，大部分是矩阵运算，而且使用嵌套for循环来执行的，所以读起来比较费劲，但是要是移植到自己工程上的话必然离不开这一步，所以花了一个下午把各个细节理清楚，顺便记录分享。

<code class="language-C hljs vala has-numbering"><span class="hljs-comment">/* Include files */</span>
<span class="hljs-preprocessor">#include "rt_nonfinite.h"</span>
<span class="hljs-preprocessor">#include "attitudeKalmanfilter.h"</span>
<span class="hljs-preprocessor">#include "rdivide.h"</span>
<span class="hljs-preprocessor">#include "norm.h"</span>
<span class="hljs-preprocessor">#include "cross.h"</span>
<span class="hljs-preprocessor">#include "eye.h"</span>
<span class="hljs-preprocessor">#include "mrdivide.h"</span>

<span class="hljs-comment">/* 
'输入参数：updateVect[3]：用来记录陀螺仪，加速度计，磁力计传感器数值是否有效
              z[9]     ：测量矩阵
    x_aposteriori_k[12]：上一时刻状态后验估计矩阵，用来预测当前状态
   P_aposteriori_k[144]：上一时刻后验估计方差
        eulerAngles[3] ：输出欧拉角
        Rot_matrix[9]  ：输出余弦矩阵
     x_aposteriori[12] ：输出状态后验估计矩阵 
    P_aposteriori[144] ：输出方差后验估计矩阵'
*/</span>
<span class="hljs-keyword">void</span> attitudeKalmanfilter(
<span class="hljs-keyword">const</span> uint8_T updateVect[<span class="hljs-number">3</span>],
real32_T dt, 
<span class="hljs-keyword">const</span> real32_T z[<span class="hljs-number">9</span>], 
<span class="hljs-keyword">const</span> real32_T x_aposteriori_k[<span class="hljs-number">12</span>], 
<span class="hljs-keyword">const</span> real32_T P_aposteriori_k[<span class="hljs-number">144</span>], 
<span class="hljs-keyword">const</span> real32_T q[<span class="hljs-number">12</span>], 
real32_T r[<span class="hljs-number">9</span>], 
real32_T eulerAngles[<span class="hljs-number">3</span>], 
real32_T Rot_matrix[<span class="hljs-number">9</span>],
real32_T x_aposteriori[<span class="hljs-number">12</span>], 
real32_T P_aposteriori[<span class="hljs-number">144</span>])
{
<span class="hljs-comment">/*以下这一堆变量用到的时候再解释*/</span>
  real32_T wak[<span class="hljs-number">3</span>];
  real32_T O[<span class="hljs-number">9</span>];
  real_T dv0[<span class="hljs-number">9</span>];
  real32_T a[<span class="hljs-number">9</span>];
  int32_T i;
  real32_T b_a[<span class="hljs-number">9</span>];
  real32_T x_n_b[<span class="hljs-number">3</span>];
  real32_T b_x_aposteriori_k[<span class="hljs-number">3</span>];
  real32_T z_n_b[<span class="hljs-number">3</span>];
  real32_T c_a[<span class="hljs-number">3</span>];
  real32_T d_a[<span class="hljs-number">3</span>];
  int32_T i0;
  real32_T x_apriori[<span class="hljs-number">12</span>];
  real_T dv1[<span class="hljs-number">144</span>];
  real32_T A_lin[<span class="hljs-number">144</span>];
  <span class="hljs-keyword">static</span> <span class="hljs-keyword">const</span> int8_T iv0[<span class="hljs-number">36</span>] = { <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span> };

  real32_T b_A_lin[<span class="hljs-number">144</span>];
  real32_T b_q[<span class="hljs-number">144</span>];
  real32_T c_A_lin[<span class="hljs-number">144</span>];
  real32_T d_A_lin[<span class="hljs-number">144</span>];
  real32_T e_A_lin[<span class="hljs-number">144</span>];
  int32_T i1;
  real32_T P_apriori[<span class="hljs-number">144</span>];
  real32_T b_P_apriori[<span class="hljs-number">108</span>];
  <span class="hljs-keyword">static</span> <span class="hljs-keyword">const</span> int8_T iv1[<span class="hljs-number">108</span>] = { <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span> };

  real32_T K_k[<span class="hljs-number">108</span>];
  real32_T fv0[<span class="hljs-number">81</span>];
  <span class="hljs-keyword">static</span> <span class="hljs-keyword">const</span> int8_T iv2[<span class="hljs-number">108</span>] = { <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>,
                                   <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span> };

  real32_T b_r[<span class="hljs-number">81</span>];
  real32_T fv1[<span class="hljs-number">81</span>];
  real32_T f0;
  real32_T c_P_apriori[<span class="hljs-number">36</span>]=
{ <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
  <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,<span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span> };

  real32_T fv2[<span class="hljs-number">36</span>];
  <span class="hljs-keyword">static</span> <span class="hljs-keyword">const</span> int8_T iv4[<span class="hljs-number">36</span>] = { <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, </code>

<code class="language-C hljs vala has-numbering">       <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span> };

  real32_T c_r[<span class="hljs-number">9</span>];
  real32_T b_K_k[<span class="hljs-number">36</span>];
  real32_T d_P_apriori[<span class="hljs-number">72</span>];
  <span class="hljs-keyword">static</span> <span class="hljs-keyword">const</span> int8_T iv5[<span class="hljs-number">72</span>] 
  = { <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
      <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
      <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
      <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span> };

  real32_T c_K_k[<span class="hljs-number">72</span>];
  <span class="hljs-keyword">static</span> <span class="hljs-keyword">const</span> int8_T iv6[<span class="hljs-number">72</span>] = { <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
                                  <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span> };

  real32_T b_z[<span class="hljs-number">6</span>];
  <span class="hljs-keyword">static</span> <span class="hljs-keyword">const</span> int8_T iv7[<span class="hljs-number">72</span>] 
  = { <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
      <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
      <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
      <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
      <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span> };

  <span class="hljs-keyword">static</span> <span class="hljs-keyword">const</span> int8_T iv8[<span class="hljs-number">72</span>]
   = { <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
       <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
       <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
       <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
       <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>,
       <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
       <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, 
       <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">1</span> };

  real32_T fv3[<span class="hljs-number">6</span>];
  real32_T c_z[<span class="hljs-number">6</span>];

  <span class="hljs-comment">/*开始计算*/</span>

  <span class="hljs-comment">/*'wak[]为当前状态三轴角加速度'*/</span>
  wak[<span class="hljs-number">0</span>] = x_aposteriori_k[<span class="hljs-number">3</span>];</code>

<code class="language-C hljs vala has-numbering"> wak[<span class="hljs-number">1</span>] = x_aposteriori_k[<span class="hljs-number">4</span>];
  wak[<span class="hljs-number">2</span>] = x_aposteriori_k[<span class="hljs-number">5</span>];</code>

<code class="language-C hljs vala has-numbering"></code><p>/* ‘欧拉角旋转矩阵’  
<span class="MathJax_Preview"></span><div class="MathJax_Display" role="textbox" aria-readonly="true" style="text-align: center;"><span class="MathJax" id="MathJax-Element-51-Frame"><nobr><span class="math" id="MathJax-Span-1" style="width: 13.58em; display: inline-block;"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 10.94em; height: 0px; font-size: 124%; display: inline-block; position: relative;"><span style="left: 0em; top: -5.01em; position: absolute; clip: rect(2.59em, 1000em, 6.92em, -0.46em);"><span class="mrow" id="MathJax-Span-2"><span class="mi" id="MathJax-Span-3" style="font-family: MathJax_Math-italic-Web;">O</span><span class="mo" id="MathJax-Span-4" style="padding-left: 0.27em; font-family: MathJax_Main-Web;">=</span><span class="mrow" id="MathJax-Span-5" style="padding-left: 0.27em;"><span class="mo" id="MathJax-Span-6" style="padding-left: 0.27em; vertical-align: 2.24em;"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 0.66em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.82em; font-family: MathJax_Size4-Web; position: absolute;">⎡ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 0em; top: -0.62em; font-family: MathJax_Size4-Web; position: absolute;">⎣ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 0em; top: -1.67em; font-family: MathJax_Size4-Web; position: absolute;">⎢ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span></span></span><span class="mtable" id="MathJax-Span-7" style="padding-right: 0.16em; padding-left: 0.16em;"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 6.97em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -4.83em; position: absolute; clip: rect(2.55em, 1000em, 6.75em, -0.49em);"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.11em; height: 0px; display: inline-block; position: relative;"><span style="left: 50%; top: -4.32em; margin-left: -0.25em; position: absolute; clip: rect(2.04em, 1000em, 3.07em, -0.47em);"><span class="mtd" id="MathJax-Span-8"><span class="mrow" id="MathJax-Span-9"><span class="mn" id="MathJax-Span-10" style="font-family: MathJax_Main-Web;">0</span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span><span style="left: 50%; top: -3.92em; margin-left: -0.55em; position: absolute; clip: rect(3.35em, 1000em, 4.3em, -0.49em);"><span class="mtd" id="MathJax-Span-22"><span class="mrow" id="MathJax-Span-23"><span class="msubsup" id="MathJax-Span-24"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.11em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.86em, 1000em, 2.66em, -0.49em);"><span class="mi" id="MathJax-Span-25" style="font-family: MathJax_Math-italic-Web;">w</span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.69em; top: -1.86em; position: absolute;"><span class="mi" id="MathJax-Span-26" style="font-family: MathJax_Math-italic-Web; font-size: 70.7%;"><span style="font-size:14px;">z</span><span style="width: 0em; height: 1px; overflow: hidden; display: inline-block;"></span></span><span style="font-family:宋体;font-size:24px;"> </span><span style="width: 0px; height: 2.01em; display: inline-block;"></span></span></span></span></span></span><span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 50%; top: -2.52em; margin-left: -0.55em; position: absolute; clip: rect(3.35em, 1000em, 4.44em, -0.49em);"><span class="mtd" id="MathJax-Span-36"><span class="mrow" id="MathJax-Span-37"><span class="msubsup" id="MathJax-Span-38"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.11em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.86em, 1000em, 2.66em, -0.49em);"><span class="mi" id="MathJax-Span-39" style="font-family: MathJax_Math-italic-Web;">w</span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.69em; top: -1.86em; position: absolute;"><span class="mi" id="MathJax-Span-40" style="font-family: MathJax_Math-italic-Web; font-size: 70.7%;"><span style="font-size:14px;">y</span><span style="width: 0em; height: 1px; overflow: hidden; display: inline-block;"></span></span><span style="font-family:宋体;font-size:24px;"> </span><span style="width: 0px; height: 2.01em; display: inline-block;"></span></span></span></span></span></span><span style="width: 0px; height: 3.97em; display: inline-block;"></span></span></span> <span style="width: 0px; height: 4.83em; display: inline-block;"></span></span><span style="left: 2.11em; top: -4.49em; position: absolute; clip: rect(2.43em, 1000em, 6.27em, -0.49em);"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.9em; height: 0px; display: inline-block; position: relative;"><span style="left: 50%; top: -4.32em; margin-left: -0.95em; position: absolute; clip: rect(2.26em, 1000em, 3.21em, -0.43em);"><span class="mtd" id="MathJax-Span-11"><span class="mrow" id="MathJax-Span-12"><span class="mo" id="MathJax-Span-13" style="font-family: MathJax_Main-Web;">−</span><span class="msubsup" id="MathJax-Span-14"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.11em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.86em, 1000em, 2.66em, -0.49em);"><span class="mi" id="MathJax-Span-15" style="font-family: MathJax_Math-italic-Web;">w</span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.69em; top: -1.86em; position: absolute;"><span class="mi" id="MathJax-Span-16" style="font-family: MathJax_Math-italic-Web; font-size: 70.7%;"><span style="font-size:14px;">z</span><span style="width: 0em; height: 1px; overflow: hidden; display: inline-block;"></span></span><span style="font-family:宋体;font-size:24px;"> </span><span style="width: 0px; height: 2.01em; display: inline-block;"></span></span></span></span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span><span style="left: 50%; top: -2.83em; margin-left: -0.25em; position: absolute; clip: rect(2.04em, 1000em, 3.07em, -0.47em);"><span class="mtd" id="MathJax-Span-27"><span class="mrow" id="MathJax-Span-28"><span class="mn" id="MathJax-Span-29" style="font-family: MathJax_Main-Web;">0</span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span><span style="left: 50%; top: -2.52em; margin-left: -0.58em; position: absolute; clip: rect(3.35em, 1000em, 4.3em, -0.49em);"><span class="mtd" id="MathJax-Span-41"><span class="mrow" id="MathJax-Span-42"><span class="msubsup" id="MathJax-Span-43"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.16em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.86em, 1000em, 2.66em, -0.49em);"><span class="mi" id="MathJax-Span-44" style="font-family: MathJax_Math-italic-Web;">w</span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.69em; top: -1.86em; position: absolute;"><span class="mi" id="MathJax-Span-45" style="font-family: MathJax_Math-italic-Web; font-size: 70.7%;"><span style="font-size:14px;">x</span></span> <span style="width: 0px; height: 2.01em; display: inline-block;"></span></span></span></span></span></span><span style="width: 0px; height: 3.97em; display: inline-block;"></span></span></span> <span style="width: 0px; height: 4.49em; display: inline-block;"></span></span><span style="left: 5.01em; top: -4.37em; position: absolute; clip: rect(2.31em, 1000em, 6.02em, -0.49em);"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.95em; height: 0px; display: inline-block; position: relative;"><span style="left: 50%; top: -5.42em; margin-left: -0.55em; position: absolute; clip: rect(3.35em, 1000em, 4.44em, -0.49em);"><span class="mtd" id="MathJax-Span-17"><span class="mrow" id="MathJax-Span-18"><span class="msubsup" id="MathJax-Span-19"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.11em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.86em, 1000em, 2.66em, -0.49em);"><span class="mi" id="MathJax-Span-20" style="font-family: MathJax_Math-italic-Web;">w</span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.69em; top: -1.86em; position: absolute;"><span class="mi" id="MathJax-Span-21" style="font-family: MathJax_Math-italic-Web; font-size: 70.7%;"><span style="font-size:14px;">y</span><span style="width: 0em; height: 1px; overflow: hidden; display: inline-block;"></span></span><span style="font-family:宋体;font-size:24px;"> </span><span style="width: 0px; height: 2.01em; display: inline-block;"></span></span></span></span></span></span><span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 50%; top: -2.83em; margin-left: -0.97em; position: absolute; clip: rect(2.26em, 1000em, 3.21em, -0.43em);"><span class="mtd" id="MathJax-Span-30"><span class="mrow" id="MathJax-Span-31"><span class="mo" id="MathJax-Span-32" style="font-family: MathJax_Main-Web;">−</span><span class="msubsup" id="MathJax-Span-33"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.16em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.86em, 1000em, 2.66em, -0.49em);"><span class="mi" id="MathJax-Span-34" style="font-family: MathJax_Math-italic-Web;">w</span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.69em; top: -1.86em; position: absolute;"><span class="mi" id="MathJax-Span-35" style="font-family: MathJax_Math-italic-Web; font-size: 70.7%;"><span style="font-size:14px;">x</span></span> <span style="width: 0px; height: 2.01em; display: inline-block;"></span></span></span></span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span><span style="left: 50%; top: -1.43em; margin-left: -0.25em; position: absolute; clip: rect(2.04em, 1000em, 3.07em, -0.47em);"><span class="mtd" id="MathJax-Span-46"><span class="mrow" id="MathJax-Span-47"><span class="mn" id="MathJax-Span-48" style="font-family: MathJax_Main-Web;">0</span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span></span> <span style="width: 0px; height: 4.37em; display: inline-block;"></span></span></span></span><span class="mo" id="MathJax-Span-49" style="vertical-align: 2.24em;"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 0.66em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.82em; font-family: MathJax_Size4-Web; position: absolute;">⎤ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 0em; top: -0.62em; font-family: MathJax_Size4-Web; position: absolute;">⎦ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 0em; top: -1.67em; font-family: MathJax_Size4-Web; position: absolute;">⎥ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span></span></span></span></span> <span style="width: 0px; height: 5.01em; display: inline-block;"></span></span></span><span style="width: 0px; height: 5.09em; overflow: hidden; vertical-align: -2.23em; border-left-color: currentColor; border-left-width: 0em; border-left-style: solid; display: inline-block;"></span></span></nobr></span></div>

 
这里的O矩阵相当于A矩阵中的<img title="" alt="这里写图片描述" src="http://img.blog.csdn.net/20150507144253458" />的转置矩阵！ 
*/</p><p></p><pre class="prettyprint" name="code"><code class="language-C hljs cpp has-numbering">  O[<span class="hljs-number">0</span>] = <span class="hljs-number">0.0F</span>;
  O[<span class="hljs-number">1</span>] = -x_aposteriori_k[<span class="hljs-number">2</span>];
  O[<span class="hljs-number">2</span>] = x_aposteriori_k[<span class="hljs-number">1</span>];
  O[<span class="hljs-number">3</span>] = x_aposteriori_k[<span class="hljs-number">2</span>];
  O[<span class="hljs-number">4</span>] = <span class="hljs-number">0.0F</span>;
  O[<span class="hljs-number">5</span>] = -x_aposteriori_k[<span class="hljs-number">0</span>];
  O[<span class="hljs-number">6</span>] = -x_aposteriori_k[<span class="hljs-number">1</span>];
  O[<span class="hljs-number">7</span>] = x_aposteriori_k[<span class="hljs-number">0</span>];
  O[<span class="hljs-number">8</span>] = <span class="hljs-number">0.0F</span>;

  <span class="hljs-comment">/* 预测转过一个小角度之后的重力向量三轴投影 */</span>

  <span class="hljs-comment">/* a = [1,      -delta_z, delta_y;
     *    delta_z,  1     , -delta_x;
     *   -delta_y, delta_x,     1  ]'; */</span>

  eye(dv0);  <span class="hljs-comment">//dv0矩阵单位化</span>
  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">9</span>; i++) {
    a[i] = (real32_T)dv0[i] + O[i] * dt;
  }

  <span class="hljs-comment">/* 预测转过一个小角度之后的磁力向量三轴投影 */</span>

  eye(dv0);
  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">9</span>; i++) {
    b_a[i] = (real32_T)dv0[i] + O[i] * dt;
  }
</code><ul class="pre-numbering" style="display: block;"><li>1</li><li>2</li><li>3</li><li>4</li><li>5</li><li>6</li><li>7</li><li>8</li><li>9</li><li>10</li><li>11</li><li>12</li><li>13</li><li>14</li><li>15</li><li>16</li><li>17</li><li>18</li><li>19</li><li>20</li><li>21</li><li>22</li><li>23</li><li>24</li><li>25</li><li>26</li><li>27</li><li>28</li></ul>

/*

a=⎡ ⎣ ⎢ 1Δz−Δy −Δz1Δx Δy−Δx1 ⎤ ⎦ ⎥  

其实就是这个大家都很眼熟的的余弦矩阵的转置, 用来更新机体转过一个角度之后的重力和磁力三轴投影，只不过两次计算间隔时间很短，变化角度很小，因此忽略高阶小量之后就变成了这个样子。这里还少一个时间系数dt，下面会补上。

⎡ ⎣ ⎢ cosy∗cosz−cosy∗sinzsiny (sinx∗siny∗cosz)+(cosx∗sinz)−(sinx∗siny∗sinz)+(cosx∗cosz)−sinx∗cosy −(cosx∗siny∗cosz)+(sinx∗sinz)(cosx∗siny∗sinz)+(sinx∗cosz)cosx∗cosy ⎤ ⎦ ⎥  

*/

<code class="language-C hljs cpp has-numbering">  x_n_b[<span class="hljs-number">0</span>] = x_aposteriori_k[<span class="hljs-number">0</span>];         <span class="hljs-comment">//角速度</span>
  x_n_b[<span class="hljs-number">1</span>] = x_aposteriori_k[<span class="hljs-number">1</span>];
  x_n_b[<span class="hljs-number">2</span>] = x_aposteriori_k[<span class="hljs-number">2</span>];
  b_x_aposteriori_k[<span class="hljs-number">0</span>] = x_aposteriori_k[<span class="hljs-number">6</span>];  <span class="hljs-comment">// 加速度</span>
  b_x_aposteriori_k[<span class="hljs-number">1</span>] = x_aposteriori_k[<span class="hljs-number">7</span>];
  b_x_aposteriori_k[<span class="hljs-number">2</span>] = x_aposteriori_k[<span class="hljs-number">8</span>];
  z_n_b[<span class="hljs-number">0</span>] = x_aposteriori_k[<span class="hljs-number">9</span>];        <span class="hljs-comment">//磁力计</span>
  z_n_b[<span class="hljs-number">1</span>] = x_aposteriori_k[<span class="hljs-number">10</span>];
  z_n_b[<span class="hljs-number">2</span>] = x_aposteriori_k[<span class="hljs-number">11</span>];
  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
    c_a[i] = <span class="hljs-number">0.0F</span>;
    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
      c_a[i] += a[i + <span class="hljs-number">3</span> * i0] * b_x_aposteriori_k[i0];
    }

    d_a[i] = <span class="hljs-number">0.0F</span>;
    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
      d_a[i] += b_a[i + <span class="hljs-number">3</span> * i0] * z_n_b[i0];
    }

    x_apriori[i] = x_n_b[i] + dt * wak[i];
  }

  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
    x_apriori[i + <span class="hljs-number">3</span>] = wak[i];
  }

  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
    x_apriori[i + <span class="hljs-number">6</span>] = c_a[i];
  }

  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
    x_apriori[i + <span class="hljs-number">9</span>] = d_a[i];
  }   <span class="hljs-comment">//得到状态先验估计  </span></code><ul class="pre-numbering" style="display: block;"><li>1</li><li>2</li><li>3</li><li>4</li><li>5</li><li>6</li><li>7</li><li>8</li><li>9</li><li>10</li><li>11</li><li>12</li><li>13</li><li>14</li><li>15</li><li>16</li><li>17</li><li>18</li><li>19</li><li>20</li><li>21</li><li>22</li><li>23</li><li>24</li><li>25</li><li>26</li><li>27</li><li>28</li><li>29</li><li>30</li><li>31</li><li>32</li><li>33</li><li>34</li></ul>

/*
根据上述矩阵运算，可以得到：

c_a[1∗3]=[a x  a y  a z  ]∗a[3∗3] 

从而：

ω ˜  k r a , k Δt[3∗1]=c_a[1∗3] T  

d_a[1∗3]=[m x  m y  m z  ]∗a[3∗3] 

从而：

ω ˜  k r m , k Δt[3∗1]=d_a[1∗3] T  

其中

[a x  a y  a z  ]和[m x  m y  m z  ]分别对应r a , k 和r m , k 的转置； 

得到状态先验估计:

X k + 1 [12∗1]=x_apriori[1∗12] T  

=[x_n_b+wak∗dt wak c_a d_a ] T  

*/

<code class="language-C hljs cpp has-numbering"><span class="hljs-comment">/* '开始计算A矩阵'*/</span>
  b_eye(dv1);
  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">12</span>; i++) {
    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
      A_lin[i0 + <span class="hljs-number">12</span> * i] = (real32_T)iv0[i0 + <span class="hljs-number">3</span> * i];
    }   <span class="hljs-comment">/*1 2 3列*/</span>

    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
      A_lin[(i0 + <span class="hljs-number">12</span> * i) + <span class="hljs-number">3</span>] = <span class="hljs-number">0.0F</span>;
    }    <span class="hljs-comment">/*3 4 5列*/</span>
  }
  <span class="hljs-comment">/*6 7 8 列*/</span>
  A_lin[<span class="hljs-number">6</span>] = <span class="hljs-number">0.0F</span>;
  A_lin[<span class="hljs-number">7</span>] = x_aposteriori_k[<span class="hljs-number">8</span>];
  A_lin[<span class="hljs-number">8</span>] = -x_aposteriori_k[<span class="hljs-number">7</span>];
  A_lin[<span class="hljs-number">18</span>] = -x_aposteriori_k[<span class="hljs-number">8</span>];
  A_lin[<span class="hljs-number">19</span>] = <span class="hljs-number">0.0F</span>;
  A_lin[<span class="hljs-number">20</span>] = x_aposteriori_k[<span class="hljs-number">6</span>];
  A_lin[<span class="hljs-number">30</span>] = x_aposteriori_k[<span class="hljs-number">7</span>];
  A_lin[<span class="hljs-number">31</span>] = -x_aposteriori_k[<span class="hljs-number">6</span>];
  A_lin[<span class="hljs-number">32</span>] = <span class="hljs-number">0.0F</span>;
  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
      A_lin[(i0 + <span class="hljs-number">12</span> * (i + <span class="hljs-number">3</span>)) + <span class="hljs-number">6</span>] = <span class="hljs-number">0.0F</span>;
    }
  }

  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
      A_lin[(i0 + <span class="hljs-number">12</span> * (i + <span class="hljs-number">6</span>)) + <span class="hljs-number">6</span>] = O[i0 + <span class="hljs-number">3</span> * i];
    }
  }

  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
      A_lin[(i0 + <span class="hljs-number">12</span> * (i + <span class="hljs-number">9</span>)) + <span class="hljs-number">6</span>] = <span class="hljs-number">0.0F</span>;
    }
  }
  <span class="hljs-comment">/*6 7 8 列*/</span>

  <span class="hljs-comment">/*9 10 11 列*/</span>
  A_lin[<span class="hljs-number">9</span>] = <span class="hljs-number">0.0F</span>;
  A_lin[<span class="hljs-number">10</span>] = x_aposteriori_k[<span class="hljs-number">11</span>];
  A_lin[<span class="hljs-number">11</span>] = -x_aposteriori_k[<span class="hljs-number">10</span>];
  A_lin[<span class="hljs-number">21</span>] = -x_aposteriori_k[<span class="hljs-number">11</span>];
  A_lin[<span class="hljs-number">22</span>] = <span class="hljs-number">0.0F</span>;
  A_lin[<span class="hljs-number">23</span>] = x_aposteriori_k[<span class="hljs-number">9</span>];
  A_lin[<span class="hljs-number">33</span>] = x_aposteriori_k[<span class="hljs-number">7</span>];
  A_lin[<span class="hljs-number">34</span>] = -x_aposteriori_k[<span class="hljs-number">9</span>];
  A_lin[<span class="hljs-number">35</span>] = <span class="hljs-number">0.0F</span>;
  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
      A_lin[(i0 + <span class="hljs-number">12</span> * (i + <span class="hljs-number">3</span>)) + <span class="hljs-number">9</span>] = <span class="hljs-number">0.0F</span>;
    }
  }
</code><span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
      A_lin[(i0 + <span class="hljs-number">12</span> * (i + <span class="hljs-number">6</span>)) + <span class="hljs-number">9</span>] = <span class="hljs-number">0.0F</span>;
    }
  }

  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
      A_lin[(i0 + <span class="hljs-number">12</span> * (i + <span class="hljs-number">9</span>)) + <span class="hljs-number">9</span>] = O[i0 + <span class="hljs-number">3</span> * i];
    }
  }
  <span class="hljs-comment">/*9 10 11 列*/</span>

/* 
根据上述矩阵运算，可以得到A_lin矩阵： 

   
    A_lin[12∗12]=⎡ ⎣ ⎢ ⎢ ⎢ 0I00 0000 A 1 0O0 A 2 00O ⎤ ⎦ ⎥ ⎥ ⎥  
   

其中各元素都是3*3的矩阵；I为单位矩阵，其中 

   
    A 1 =⎡ ⎣ ⎢ 0−a z a y  a z 0−a x  −a y a x 0 ⎤ ⎦ ⎥ =−r ˜  a , T k  
   

同样

   
    A 2 =⎡ ⎣ ⎢ 0−m z m y  m z 0−m x  −m y m x 0 ⎤ ⎦ ⎥ =−r ˜  m , T k  
   

*/

<code class="language-C hljs cs has-numbering">  <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">12</span>; i++) {
    <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">12</span>; i0++) {
      b_A_lin[i0 + <span class="hljs-number">12</span> * i] = (real32_T)dv1[i0 + <span class="hljs-number">12</span> * i] +         A_lin[i0 + <span class="hljs-number">12</span> * i] *dt;   
    }
  }   <span class="hljs-comment">//最终A_link,k的逆矩阵</span></code><ul class="pre-numbering" style="display: block;"><li>1</li><li>2</li><li>3</li><li>4</li><li>5</li></ul>

得到： 

   
    A l in, T k =b_A_lin[12∗12]=⎡ ⎣ ⎢ ⎢ ⎢ I000 0I00 00I0 000I ⎤ ⎦ ⎥ ⎥ ⎥ +⎡ ⎣ ⎢ ⎢ ⎢ 0I00 0000 A 1 0O0 A 2 00O ⎤ ⎦ ⎥ ⎥ ⎥ ∗dt 
   

/* 
开始根据计算过程方差 
*/ 

   
    过程噪声方差b_q[12∗12]=⎡ ⎣ ⎢ ⎢ ⎢ ⎢ q 0 000 0q 1 00 00q 2 0 000q 3  ⎤ ⎦ ⎥ ⎥ ⎥ ⎥  
   

<span class="hljs-comment">

其中各元素都是3*3的矩阵；</span>

<span class="hljs-comment"> b_r[<span class="hljs-number">0</span>] = r[<span class="hljs-number">0</span>];
    b_r[<span class="hljs-number">9</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">18</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">27</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">36</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">45</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">54</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">63</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">72</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">1</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">10</span>] = r[<span class="hljs-number">0</span>];
    b_r[<span class="hljs-number">19</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">28</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">37</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">46</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">55</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">64</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">73</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">2</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">11</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">20</span>] = r[<span class="hljs-number">0</span>];
    b_r[<span class="hljs-number">29</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">38</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">47</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">56</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">65</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">74</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">3</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">12</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">21</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">30</span>] = r[<span class="hljs-number">1</span>];
    b_r[<span class="hljs-number">39</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">48</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">57</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">66</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">75</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">4</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">13</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">22</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">31</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">40</span>] = r[<span class="hljs-number">1</span>];
    b_r[<span class="hljs-number">49</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">58</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">67</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">76</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">5</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">14</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">23</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">32</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">41</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">50</span>] = r[<span class="hljs-number">1</span>];
    b_r[<span class="hljs-number">59</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">68</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">77</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">6</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">15</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">24</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">33</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">42</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">51</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">60</span>] = r[<span class="hljs-number">2</span>];
    b_r[<span class="hljs-number">69</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">78</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">7</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">16</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">25</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">34</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">43</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">52</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">61</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">70</span>] = r[<span class="hljs-number">2</span>];
    b_r[<span class="hljs-number">79</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">8</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">17</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">26</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">35</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">44</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">53</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">62</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">71</span>] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
    b_r[<span class="hljs-number">80</span>] = r[<span class="hljs-number">2</span>];
    <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">9</span>; i++) {
      <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">9</span>; i0++) {
        fv1[i0 + <span class="hljs-number">9</span> * i] = fv0[i0 + <span class="hljs-number">9</span> *i] + b_r[i0 + <span class="hljs-number">9</span> * i];
      }
    }</span>

<span class="hljs-comment"></span><div class="MathJax_Display" role="textbox" aria-readonly="true" style="text-align: center;"><span class="MathJax" id="MathJax-Element-25-Frame"><nobr><span class="math" id="MathJax-Span-1616" style="width: 29.94em; display: inline-block;"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 24.13em; height: 0px; font-size: 124%; display: inline-block; position: relative;"><span style="left: 0em; top: -4.78em; position: absolute; clip: rect(2.45em, 1000em, 6.6em, -0.46em);"><span class="mrow" id="MathJax-Span-1617"><span class="mi" id="MathJax-Span-1618" style="font-family: MathJax_Math-italic-Web;">f<span style="width: 0.06em; height: 1px; overflow: hidden; display: inline-block;"></span></span><span class="mi" id="MathJax-Span-1619" style="font-family: MathJax_Math-italic-Web;">v</span><span class="mn" id="MathJax-Span-1620" style="font-family: MathJax_Main-Web;">1</span><span class="mo" id="MathJax-Span-1621" style="font-family: MathJax_Main-Web;">[</span><span class="mn" id="MathJax-Span-1622" style="font-family: MathJax_Main-Web;">9</span><span class="mo" id="MathJax-Span-1623" style="padding-left: 0.22em; font-family: MathJax_Main-Web;">∗</span><span class="mn" id="MathJax-Span-1624" style="padding-left: 0.22em; font-family: MathJax_Main-Web;">9</span><span class="mo" id="MathJax-Span-1625" style="font-family: MathJax_Main-Web;">]</span><span class="mo" id="MathJax-Span-1626" style="padding-left: 0.27em; font-family: MathJax_Main-Web;">=</span><span class="mi" id="MathJax-Span-1627" style="padding-left: 0.27em; font-family: MathJax_Math-italic-Web;">f<span style="width: 0.06em; height: 1px; overflow: hidden; display: inline-block;"></span></span><span class="mi" id="MathJax-Span-1628" style="font-family: MathJax_Math-italic-Web;">v</span><span class="mn" id="MathJax-Span-1629" style="font-family: MathJax_Main-Web;">0</span><span class="mo" id="MathJax-Span-1630" style="font-family: MathJax_Main-Web;">[</span><span class="mn" id="MathJax-Span-1631" style="font-family: MathJax_Main-Web;">9</span><span class="mo" id="MathJax-Span-1632" style="padding-left: 0.22em; font-family: MathJax_Main-Web;">∗</span><span class="mn" id="MathJax-Span-1633" style="padding-left: 0.22em; font-family: MathJax_Main-Web;">9</span><span class="mo" id="MathJax-Span-1634" style="font-family: MathJax_Main-Web;">]</span><span class="mo" id="MathJax-Span-1635" style="padding-left: 0.22em; font-family: MathJax_Main-Web;">+</span><span class="mrow" id="MathJax-Span-1636" style="padding-left: 0.22em;"><span class="mo" id="MathJax-Span-1637" style="padding-left: 0.22em; vertical-align: 2.15em;"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 0.66em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.82em; font-family: MathJax_Size4-Web; position: absolute;">⎡ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 0em; top: -0.81em; font-family: MathJax_Size4-Web; position: absolute;">⎣ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 0em; top: -1.77em; font-family: MathJax_Size4-Web; position: absolute;">⎢ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span></span></span><span class="mtable" id="MathJax-Span-1638" style="padding-right: 0.16em; padding-left: 0.16em;"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 4.64em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -4.26em; position: absolute; clip: rect(2.29em, 1000em, 5.9em, -0.49em);"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 0.88em; height: 0px; display: inline-block; position: relative;"><span style="left: 50%; top: -5.32em; margin-left: -0.44em; position: absolute; clip: rect(3.36em, 1000em, 4.31em, -0.49em);"><span class="mtd" id="MathJax-Span-1639"><span class="mrow" id="MathJax-Span-1640"><span class="msubsup" id="MathJax-Span-1641"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 0.88em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.86em, 1000em, 2.66em, -0.49em);"><span class="mi" id="MathJax-Span-1642" style="font-family: MathJax_Math-italic-Web;">r</span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.46em; top: -2.03em; position: absolute;"><span class="mn" id="MathJax-Span-1643" style="font-family: MathJax_Main-Web; font-size: 70.7%;"><span style="font-size:14px;">0</span></span> <span style="width: 0px; height: 2.18em; display: inline-block;"></span></span></span></span></span></span><span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 50%; top: -2.83em; margin-left: -0.25em; position: absolute; clip: rect(2.04em, 1000em, 3.07em, -0.47em);"><span class="mtd" id="MathJax-Span-1650"><span class="mrow" id="MathJax-Span-1651"><span class="mn" id="MathJax-Span-1652" style="font-family: MathJax_Main-Web;">0</span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span><span style="left: 50%; top: -1.43em; margin-left: -0.25em; position: absolute; clip: rect(2.04em, 1000em, 3.07em, -0.47em);"><span class="mtd" id="MathJax-Span-1661"><span class="mrow" id="MathJax-Span-1662"><span class="mn" id="MathJax-Span-1663" style="font-family: MathJax_Main-Web;">0</span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span></span> <span style="width: 0px; height: 4.26em; display: inline-block;"></span></span><span style="left: 1.88em; top: -4.49em; position: absolute; clip: rect(2.3em, 1000em, 6.13em, -0.49em);"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 0.88em; height: 0px; display: inline-block; position: relative;"><span style="left: 50%; top: -4.23em; margin-left: -0.25em; position: absolute; clip: rect(2.04em, 1000em, 3.07em, -0.47em);"><span class="mtd" id="MathJax-Span-1644"><span class="mrow" id="MathJax-Span-1645"><span class="mn" id="MathJax-Span-1646" style="font-family: MathJax_Main-Web;">0</span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span><span style="left: 50%; top: -3.92em; margin-left: -0.44em; position: absolute; clip: rect(3.36em, 1000em, 4.29em, -0.49em);"><span class="mtd" id="MathJax-Span-1653"><span class="mrow" id="MathJax-Span-1654"><span class="msubsup" id="MathJax-Span-1655"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 0.88em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.86em, 1000em, 2.66em, -0.49em);"><span class="mi" id="MathJax-Span-1656" style="font-family: MathJax_Math-italic-Web;">r</span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.46em; top: -2.03em; position: absolute;"><span class="mn" id="MathJax-Span-1657" style="font-family: MathJax_Main-Web; font-size: 70.7%;"><span style="font-size:14px;">1</span></span> <span style="width: 0px; height: 2.18em; display: inline-block;"></span></span></span></span></span></span><span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 50%; top: -1.43em; margin-left: -0.25em; position: absolute; clip: rect(2.04em, 1000em, 3.07em, -0.47em);"><span class="mtd" id="MathJax-Span-1664"><span class="mrow" id="MathJax-Span-1665"><span class="mn" id="MathJax-Span-1666" style="font-family: MathJax_Main-Web;">0</span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span></span> <span style="width: 0px; height: 4.49em; display: inline-block;"></span></span><span style="left: 3.76em; top: -4.6em; position: absolute; clip: rect(2.41em, 1000em, 6.38em, -0.49em);"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 0.88em; height: 0px; display: inline-block; position: relative;"><span style="left: 50%; top: -4.23em; margin-left: -0.25em; position: absolute; clip: rect(2.04em, 1000em, 3.07em, -0.47em);"><span class="mtd" id="MathJax-Span-1647"><span class="mrow" id="MathJax-Span-1648"><span class="mn" id="MathJax-Span-1649" style="font-family: MathJax_Main-Web;">0</span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span><span style="left: 50%; top: -2.83em; margin-left: -0.25em; position: absolute; clip: rect(2.04em, 1000em, 3.07em, -0.47em);"><span class="mtd" id="MathJax-Span-1658"><span class="mrow" id="MathJax-Span-1659"><span class="mn" id="MathJax-Span-1660" style="font-family: MathJax_Main-Web;">0</span></span></span><span style="width: 0px; height: 2.88em; display: inline-block;"></span></span><span style="left: 50%; top: -2.52em; margin-left: -0.44em; position: absolute; clip: rect(3.36em, 1000em, 4.29em, -0.49em);"><span class="mtd" id="MathJax-Span-1667"><span class="mrow" id="MathJax-Span-1668"><span class="msubsup" id="MathJax-Span-1669"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 0.88em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.86em, 1000em, 2.66em, -0.49em);"><span class="mi" id="MathJax-Span-1670" style="font-family: MathJax_Math-italic-Web;">r</span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.46em; top: -2.03em; position: absolute;"><span class="mn" id="MathJax-Span-1671" style="font-family: MathJax_Main-Web; font-size: 70.7%;"><span style="font-size:14px;">2</span></span> <span style="width: 0px; height: 2.18em; display: inline-block;"></span></span></span></span></span></span><span style="width: 0px; height: 3.97em; display: inline-block;"></span></span></span> <span style="width: 0px; height: 4.6em; display: inline-block;"></span></span></span></span><span class="mo" id="MathJax-Span-1672" style="vertical-align: 2.15em;"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 0.66em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.82em; font-family: MathJax_Size4-Web; position: absolute;">⎤ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 0em; top: -0.81em; font-family: MathJax_Size4-Web; position: absolute;">⎦ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span><span style="left: 0em; top: -1.77em; font-family: MathJax_Size4-Web; position: absolute;">⎥ <span style="width: 0px; height: 3.97em; display: inline-block;"></span></span></span></span></span><span class="mo" id="MathJax-Span-1673" style="padding-left: 0.27em; font-family: MathJax_Main-Web;">=</span><span class="msubsup" id="MathJax-Span-1674" style="padding-left: 0.27em;"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.22em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.62em, 1000em, 2.65em, -0.48em);"><span class="mi" id="MathJax-Span-1675" style="font-family: MathJax_Math-italic-Web;">H<span style="width: 0.05em; height: 1px; overflow: hidden; display: inline-block;"></span></span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.8em; top: -1.86em; position: absolute;"><span class="mi" id="MathJax-Span-1676" style="font-family: MathJax_Math-italic-Web; font-size: 70.7%;"><span style="font-size:14px;">k</span></span> <span style="width: 0px; height: 2.01em; display: inline-block;"></span></span></span></span><span class="msubsup" id="MathJax-Span-1677"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.06em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.62em, 1000em, 2.65em, -0.48em);"><span class="mi" id="MathJax-Span-1678" style="font-family: MathJax_Math-italic-Web;">P<span style="width: 0.1em; height: 1px; overflow: hidden; display: inline-block;"></span></span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.64em; top: -1.86em; position: absolute;"><span class="mi" id="MathJax-Span-1679" style="font-family: MathJax_Math-italic-Web; font-size: 70.7%;"><span style="font-size:14px;">k</span></span> <span style="width: 0px; height: 2.01em; display: inline-block;"></span></span></span></span><span class="msubsup" id="MathJax-Span-1680"><span style="width: 1px; height: 0px; overflow: hidden; margin-right: -1px; display: inline-block;"></span><span style="width: 1.46em; height: 0px; display: inline-block; position: relative;"><span style="left: 0em; top: -2.47em; position: absolute; clip: rect(1.62em, 1000em, 2.65em, -0.48em);"><span class="mi" id="MathJax-Span-1681" style="font-family: MathJax_Math-italic-Web;">H<span style="width: 0.05em; height: 1px; overflow: hidden; display: inline-block;"></span></span> <span style="width: 0px; height: 2.47em; display: inline-block;"></span></span><span style="left: 0.93em; top: -2.42em; position: absolute; clip: rect(1.36em, 1000em, 2.18em, -0.5em);"><span class="mi" id="MathJax-Span-1682" style="font-family: MathJax_Math-italic-Web; font-size: 70.7%;"><span style="font-size:14px;">T</span><span style="width: 0.08em; height: 1px; overflow: hidden; display: inline-block;"></span></span><span style="font-size:24px;"> </span><span style="width: 0px; height: 2.01em; display: inline-block;"></span></span><span style="left: 0.8em; top: -1.75em; position: absolute; clip: rect(1.35em, 1000em, 2.19em, -0.48em);"><span class="mi" id="MathJax-Span-1683" style="font-family: MathJax_Math-italic-Web; font-size: 70.7%;"><span style="font-size:14px;">k</span></span> <span style="width: 0px; height: 2.01em; display: inline-block;"></span></span></span></span><span class="mo" id="MathJax-Span-1684" style="padding-left: 0.22em; font-family: MathJax_Main-Web;">+</span><span class="mi" id="MathJax-Span-1685" style="padding-left: 0.22em; font-family: MathJax_Math-italic-Web;">R</span></span> <span style="width: 0px; height: 4.78em; display: inline-block;"></span></span></span><span style="width: 0px; height: 4.85em; overflow: hidden; vertical-align: -2.11em; border-left-color: currentColor; border-left-width: 0em; border-left-style: solid; display: inline-block;"></span></span></nobr></span></div>

<p></p><pre class="prettyprint" name="code"><code class="language-C hljs scss has-numbering">    <span class="hljs-comment">/*矩 阵 除 法 ，计算出卡尔曼增益*/</span>
    <span class="hljs-function">mrdivide(b_P_apriori, fv1, K_k)</span>;</code><ul class="pre-numbering" style="display: block;"><li>1</li><li>2</li></ul>

这个函数的作用是计算卡尔曼增益：K k [12∗9] T =K_K[9∗12]=b_P_apriori[9∗12]fv1[9∗9]  

<code class="language-C hljs cpp has-numbering"><span class="hljs-comment">/* x_aposteriori=x_apriori+K_k*y_k; */</span>
    <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">9</span>; i++) {
      f0 = <span class="hljs-number">0.0F</span>;
      <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">12</span>; i0++) {
        f0 += (real32_T)iv2[i + <span class="hljs-number">9</span> * i0] * x_apriori[i0];
      }

      O[i] = z[i] - f0;
    }

    <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">12</span>; i++) {
      f0 = <span class="hljs-number">0.0F</span>;
      <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">9</span>; i0++) {
        f0 += K_k[i + <span class="hljs-number">12</span> * i0] * O[i0];
      }

      x_aposteriori[i] = x_apriori[i] + f0;
    }</code><ul class="pre-numbering" style="display: block;"><li>1</li><li>2</li><li>3</li><li>4</li><li>5</li><li>6</li><li>7</li><li>8</li><li>9</li><li>10</li><li>11</li><li>12</li><li>13</li><li>14</li><li>15</li><li>16</li><li>17</li><li>18</li></ul>

计算状态后验估计：

O[1∗9]=z[1∗9]−x_apriori[1∗12]∗H T [12∗9] 

得到:

x ^  k [12∗1] T =x_aposteriori[1∗12] 

=x_apriori[1∗12]+O[1∗9]∗K_K[9∗12] 

<code class="language-C hljs perl has-numbering">    /* <span class="hljs-string">'attitudeKalmanfilter:137'</span> P_aposteriori=(eye(<span class="hljs-number">12</span>)-K_k<span class="hljs-variable">*H_k</span>)<span class="hljs-variable">*P_apriori</span>; <span class="hljs-variable">*/</span>
    b_eye(dv1);
    <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">12</span>; i++) {
      <span class="hljs-keyword">for</span> (i<span class="hljs-number">0</span> = <span class="hljs-number">0</span>; i<span class="hljs-number">0</span> < <span class="hljs-number">12</span>; i<span class="hljs-number">0</span>++) {
        f<span class="hljs-number">0</span> = <span class="hljs-number">0</span>.0F;
        <span class="hljs-keyword">for</span> (i1 = <span class="hljs-number">0</span>; i1 < <span class="hljs-number">9</span>; i1++) {
          f<span class="hljs-number">0</span> += K_k[i + <span class="hljs-number">12</span> * i1] * (real32_T)iv2[i1 + <span class="hljs-number">9</span> * i<span class="hljs-number">0</span>];
        }

        b_A_lin[i + <span class="hljs-number">12</span> * i<span class="hljs-number">0</span>] = (real32_T)dv1[i + <span class="hljs-number">12</span> * i<span class="hljs-number">0</span>] - f<span class="hljs-number">0</span>;
      }
    }

    <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">12</span>; i++) {
      <span class="hljs-keyword">for</span> (i<span class="hljs-number">0</span> = <span class="hljs-number">0</span>; i<span class="hljs-number">0</span> < <span class="hljs-number">12</span>; i<span class="hljs-number">0</span>++) {
        P_aposteriori[i + <span class="hljs-number">12</span> * i<span class="hljs-number">0</span>] = <span class="hljs-number">0</span>.0F;
        <span class="hljs-keyword">for</span> (i1 = <span class="hljs-number">0</span>; i1 < <span class="hljs-number">12</span>; i1++) {
          P_aposteriori[i + <span class="hljs-number">12</span> * i<span class="hljs-number">0</span>] += b_A_lin[i + <span class="hljs-number">12</span> * i1] * P_apriori[i1 + <span class="hljs-number">12</span>
            * i<span class="hljs-number">0</span>];
        }
      }
    }
  }</code><ul class="pre-numbering" style="display: block;"><li>1</li><li>2</li><li>3</li><li>4</li><li>5</li><li>6</li><li>7</li><li>8</li><li>9</li><li>10</li><li>11</li><li>12</li><li>13</li><li>14</li><li>15</li><li>16</li><li>17</li><li>18</li><li>19</li><li>20</li><li>21</li><li>22</li><li>23</li></ul>

计算方差后验估计：

b_A_lin[12∗12]=⎡ ⎣ ⎢ ⎢ ⎢ I000 0I00 00I0 000I ⎤ ⎦ ⎥ ⎥ ⎥ −H T k ∗K_K 

得到:

P k [12∗12] T =P_aposteriori[12∗12] 

=P_apriori[12∗12]∗b_A_lin[12∗12]; 

到此就把所有的量都计算出来了！

下面几种情形为某个传感器未更新的情况，只需改变H矩阵和测量噪声方差矩阵即可，其余运算均类似！

<code class="language-C hljs r has-numbering"><span class="hljs-keyword">else</span> {
    /* <span class="hljs-string">'attitudeKalmanfilter:138'</span> <span class="hljs-keyword">else</span> */
    /* <span class="hljs-string">'attitudeKalmanfilter:139'</span> <span class="hljs-keyword">if</span> updateVect(<span class="hljs-number">1</span>)==<span class="hljs-number">1</span>&&updateVect(<span class="hljs-number">2</span>)==<span class="hljs-number">0</span>&&updateVect(<span class="hljs-number">3</span>)==<span class="hljs-number">0</span> */
    <span class="hljs-keyword">if</span> ((updateVect[<span class="hljs-number">0</span>] == <span class="hljs-number">1</span>) && (updateVect[<span class="hljs-number">1</span>] == <span class="hljs-number">0</span>) && (updateVect[<span class="hljs-number">2</span>] == <span class="hljs-number">0</span>)) {
      /* <span class="hljs-string">'attitudeKalmanfilter:141'</span> R=[r(<span class="hljs-number">1</span>),<span class="hljs-number">0</span>,<span class="hljs-number">0</span>; */
      /* <span class="hljs-string">'attitudeKalmanfilter:142'</span>             <span class="hljs-number">0</span>,r(<span class="hljs-number">1</span>),<span class="hljs-number">0</span>; */
      /* <span class="hljs-string">'attitudeKalmanfilter:143'</span>             <span class="hljs-number">0</span>,<span class="hljs-number">0</span>,r(<span class="hljs-number">1</span>)]; */
      /* observation matrix */
      /* <span class="hljs-string">'attitudeKalmanfilter:146'</span> H_k=[  E,     Z,      Z,    Z]; */
      /* <span class="hljs-string">'attitudeKalmanfilter:148'</span> y_k=z(<span class="hljs-number">1</span>:<span class="hljs-number">3</span>)-H_k(<span class="hljs-number">1</span>:<span class="hljs-number">3</span>,<span class="hljs-number">1</span>:<span class="hljs-number">12</span>)*x_apriori; */
      /* <span class="hljs-string">'attitudeKalmanfilter:150'</span> S_k=H_k(<span class="hljs-number">1</span>:<span class="hljs-number">3</span>,<span class="hljs-number">1</span>:<span class="hljs-number">12</span>)*P_apriori*H_k(<span class="hljs-number">1</span>:<span class="hljs-number">3</span>,<span class="hljs-number">1</span>:<span class="hljs-number">12</span>)<span class="hljs-string">'+R(1:3,1:3); */
      /* '</span>attitudeKalmanfilter:<span class="hljs-number">151</span><span class="hljs-string">' K_k=(P_apriori*H_k(1:3,1:12)'</span>/(S_k)); */
      <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">12</span>; i++) {
        <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
          c_P_apriori[i + <span class="hljs-number">12</span> * i0] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
          <span class="hljs-keyword">for</span> (i1 = <span class="hljs-number">0</span>; i1 < <span class="hljs-number">12</span>; i1++) {
            c_P_apriori[i + <span class="hljs-number">12</span> * i0] += P_apriori[i + <span class="hljs-number">12</span> * i1] * (real32_T)
              iv3[i1 + <span class="hljs-number">12</span> * i0];
          }
        }
      }

      <span class="hljs-keyword">for</span> (i = <span class="hljs-number">0</span>; i < <span class="hljs-number">3</span>; i++) {
        <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">12</span>; i0++) {
          fv2[i + <span class="hljs-number">3</span> * i0] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
          <span class="hljs-keyword">for</span> (i1 = <span class="hljs-number">0</span>; i1 < <span class="hljs-number">12</span>; i1++) {
            fv2[i + <span class="hljs-number">3</span> * i0] += (real32_T)iv4[i + <span class="hljs-number">3</span> * i1] * P_apriori[i1 + <span class="hljs-number">12</span> *
              i0];
          }
        }

        <span class="hljs-keyword">for</span> (i0 = <span class="hljs-number">0</span>; i0 < <span class="hljs-number">3</span>; i0++) {
          O[i + <span class="hljs-number">3</span> * i0] = <span class="hljs-number">0.</span>0<span class="hljs-literal">F</span>;
          <span class="hljs-keyword">for</span> (i1 = <span class="hljs-number">0</span>; i1 < <span class="hljs-number">12</span>; i1++) {
            O[i + <span class="hljs-number">3</span> * i0] += fv2</code>

</pre>