SRM 543
div1 250
令f[X] = 1^2^3^......^X;
找规律发现X= 1, 2, ... 20. The sequence is {1, 3, 0, 4, 1, 7, 0, 8, 1, 11, 0, 12, 1, 15, 0, 16, 1, 19, 0, 20}
Can you see it?If X mod 4 == 0, then X. If X mod 4 == 1 then 1. If X mod 4 == 2 then X+1. If X mod 4 == 3 then 0.
然后秒过:
public class EllysXors
{
long xor1N(long N)
{
if (N % 4 == 0) return N;
if (N % 4 == 1) return 1;
if (N % 4 == 2) return N + 1;
return 0;
}
public long getXor(long L, long R)
{
return xor1N(R) ^ xor1N(L - 1);
}
};
div2 1000
递归三次+三分,详见代码
int a[3][2];
int w;
double dfs(int id, double len)
{
if(id>=3)return len/(double)w;
double l = 0.0, r = len;
double ans = 200000000.0;
for(int i = 0; i < 100; i++)
{
double m1=l+(r-l)/3.0;
double m2=r-(r-l)/3.0;
double a1 = dfs(id+1, len-m1)+sqrt(a[id][0]*a[id][0]+m1*m1)/a[id][1];
ans = min(ans, a1);
double a2 = dfs(id+1, len-m2)+sqrt(a[id][0]*a[id][0]+m2*m2)/a[id][1];
ans = min(ans, a2);
if(a1<a2)r = m2;
else l=m1;
}
return ans;
}
double EllysThreeRivers::getMin(int length, int walk, vector <int> width, vector <int> swim) {
for(int i = 0; i < 3; i++)
{
a[i][0]=width[i];
a[i][1]=swim[i];
}
w = walk;
return dfs(0, length);
}
div1 550
DP
f[i][j]表示在第 i 个岛的 j 高度处花费的最少时间
需要注意的是状态数有50*100000,所以状态转移必须在O(1)的时间内解决
1.要转移到i+1岛上的j位置,i岛上的位置从0到max一定是一个凹函数,并设i岛上的这个凹点为k位置;
2.要转移到i+1岛上的j+1位置,i岛上的位置一定是从k开始找;
关于1的证明:
我们知道f[i][k+1] > f[i][k] > f[i][k-1]
并且 k+1 -> j < k -> j < k-1 -> j
所以必然存在一个k使得f[i][k]+(k -> j)<f[i][k+1]+(k+1 -> j)且f[i][k]+(k -> j)<f[i][k-1]+(k-1 -> j);(所以是凹函数)
关于2的证明:
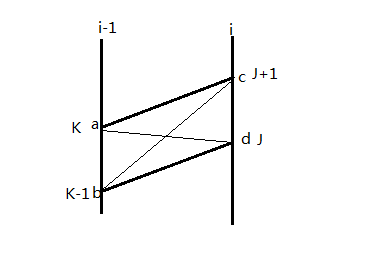
因为 f[i-1][k]+ad < f[i-1][k-1]+bd;
假设从k-1出发到J+1比从k出发更优,
即:f[i-1][k-1]+bc<f[i-1][k]+ac;
联立上面两式可得:ad+bc<bd+ac;
又因为ao+oc>ac
bo+od>bd
联立可得ad+bc>bd+ac
矛盾,所以假设不成立,所以从k出发到J+1更优!
证毕。
class EllysRivers {
public:
double getMin(int, int, vector <int>, vector <int>);
};
double f[55][100010];
double EllysRivers::getMin(int length, int walk, vector <int> width, vector <int> speed) {
int n = width.size();
memset(f,0,sizeof(f));
for(int i = 0; i <= length; i++)f[0][i]=(double)i/(double)walk;
for(int i = 0; i < n; i++)
{
int k = 0;
for(int j = 0; j <= length; j++)
{
while(k<length&&f[i][k]+sqrt((double)(j-k)*(j-k)+(double)width[i]*width[i])/(double)speed[i]>
f[i][k+1]+sqrt((double)(j-k-1)*(j-k-1)+(double)width[i]*width[i])/(double)speed[i])
{
k++;
}
f[i+1][j]=f[i][k]+sqrt((double)(j-k)*(j-k)+(double)width[i]*width[i])/(double)speed[i];
} //(j-k)*(j-k)可能会超int
}
return f[n][length];
}