hdu3802 Ipad,IPhone
Ipad,IPhone
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0
Problem Description
In ACM_DIY, there is one master called “Lost”. As we know he is a “-2Dai”, which means he has a lot of money.
Well, Lost use Ipad and IPhone to reward the ones who solve the following problem.

In this problem, we define F( n ) as :
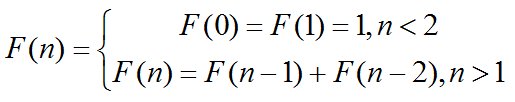
Then Lost denote a function G(a,b,n,p) as

Here a, b, n, p are all positive integer!
If you could tell Lost the value of G(a,b,n,p) , then you will get one Ipad and one IPhone!
Input
The first line is one integer T indicates the number of the test cases. (T <= 100)
Then for every case, only one line containing 4 positive integers a, b, n and p.
(1 ≤a, b, n, p≤2*10 9 , p is an odd prime number and a,b < p.)
Output
Output one line,the value of the G(a,b,n,p) .
Sample Input
4
2 3 1 10007
2 3 2 10007
2 3 3 10007
2 3 4 10007
Sample Output
40
392
3880
9941
Author
AekdyCoin
Source
ACM-DIY Group Contest 2011 Spring
Recommend
notonlysuccess
先膜拜下AC 的 1004 ……
这题错了好多次……orz ,没有注意到负数的取余,表示遗憾。
首先应该知道这么个公式
![]()
感谢zsasuke提出的错误,后来查了一下,这个公式的使用是有前提条件的:“c>phi(p)”,所以需要加个判断,如果c<=phi(p),说明c次方在O(logc)的范围内可以得出结果,因此可以直接暴力求解,大于的话才使用这个公式,对于这个公式的正确性我这几天试着证明下,是在别人的解题报告里看的这个公式,做FOJ1759的时候记下来的,并没有证明……
还有p是质数(题目给定的,没发现,感谢bstw111提出)所以phi(p)=p-1。
所以Fib(n) 次方就可以处理了。
对于后面那坨……
注意对于zn 的矩阵可能系数为负的,不能直接取模……
代码如下,表示写的很丑- -|||
#include <stdio.h> #include <math.h> #include <string.h> typedef struct { __int64 m[2][2]; }Matrix; bool check[200005]; __int64 prime[100000]; __int64 up; __int64 a,b,n,p,ok; __int64 Fumod(__int64 t,__int64 mod) { while(t<0) { t=t+mod*1000000; } t=t%mod; return t; } Matrix Mul(Matrix x,Matrix y,__int64 mod) { __int64 i,j,k; Matrix ret; for (i=0;i<2;i++) { for (j=0;j<2;j++) { ret.m[i][j]=0; for (k=0;k<2;k++) { ret.m[i][j]=(ret.m[i][j]+x.m[i][k]*y.m[k][j]); if (ret.m[i][j]>=mod) ok=1; } if (ret.m[i][j]>=0) ret.m[i][j]%=mod; else { ret.m[i][j]=Fumod(ret.m[i][j],mod); } } } return ret; } __int64 Fib(__int64 t,__int64 mod) { Matrix x,ans; x.m[0][0]=x.m[0][1]=x.m[1][0]=1; x.m[1][1]=0; ans.m[0][0]=1; ans.m[0][1]=ans.m[1][0]=ans.m[1][1]=0; while(t!=0) { if (t & 1) { ans=Mul(x,ans,mod); } t>>=1; x=Mul(x,x,mod); } return ans.m[0][0]; } void Pri() { __int64 i,k,j; up=0; memset(check,true,sizeof(check)); for (i=2;i<=200000;i++) { if (check[i]==false) continue; for (j=i;i*j<=200000;j++) { check[i*j]=false; } prime[up++]=i; } } __int64 CountZ(__int64 t,__int64 mod) { Matrix x,ans; x.m[0][0]=2*(a+b)%mod; x.m[0][1]=Fumod(-(a-b)*(a-b),mod); x.m[1][0]=1; x.m[1][1]=0; ans.m[0][0]=2*(a+b)%mod; ans.m[1][0]=2; ans.m[0][1]=ans.m[1][1]=0; while(t!=0) { if (t & 1) { ans=Mul(x,ans,mod); } t>>=1; x=Mul(x,x,mod); } return ans.m[0][0]; } __int64 FMul(__int64 x,__int64 t,__int64 mod) { __int64 ans=1; while(t!=0) { if (t & 1) { ans=ans*x%mod; } t>>=1; x=(x*x)%mod; } return ans; } int main() { __int64 i,j,T,f,z,amul,bmul,php; scanf("%I64d",&T); Pri(); while(T--) { scanf("%I64d%I64d%I64d%I64d",&a,&b,&n,&p); ok=0; php=p-1; f=Fib(n,php); if (ok==1) f+=php; z=CountZ(f-1,p); amul=(FMul(a,(p-1)/2,p)+1); bmul=(FMul(b,(p-1)/2,p)+1); printf("%I64d/n",(amul*bmul%p)*z%p); } return 0; }
