求凸包以及距离最远点对
求凸包以及距离最远点对
分类: 算法
2012-05-22 19:19
516人阅读
评论(0)
收藏
举报
算法 ini n2
otating alipers homepage
Some history:
In 1978, M.I. Shamos's Ph.D. thesis "Computational Geometry" marks the "birth" of the field within Computer Science. Among the results he presents is a very simple algorithm for finding the diameter of a convex polygon, i.e. the greatest distance determined a pair of points belonging to the polygon.The diameter turns out to be determined by an anti-podal pair of points. Shamos provides a simple O(n) time algorithm for determining the anti-podal pairs of a convex n -gon. Since there are at most 3 n /2 of these, the diameter can then be found in O(n) time.
As Toussaint later put it, Shamos' algorithm resembles rotating a pair of calipers around the polygon. Thus the term "Rotating Calipers". In 1983, Toussaint presents a paper in which a variety of problems are solved using the same technique. Since then, new algorithms based on the paradigm have been obtained, solving a multitude of problems.
They include:
- Computing distances
- The diameter of a convex polygon
- The width of a convex polygon
- The maximum distance between 2 convex polygons
- The minimum distance between 2 convex polygons
- Enclosing rectangles
- The minimum area enclosing rectangle
- The minimum perimeter enclosing rectangle
- Triangulations
- Onion triangulations
- Spiral triangulations
- Quadrangulations
- Properties of convex polygons
- Merging convex hulls
- Finding common tangents
- Intersecting convex polygons
- Critical support lines
- Vector sums of convex polygons
- Thinnest transversals
- Thinnest-strip transversals
Thesis
My Master's Thesis, Computational Geometry with the Rotating Calipers (in Postscript format) gathers the above problems, while providing details and proofs. The bibliography is available here for viewing.Applet
To use the Rotating Calipers and solve many of the above problems yourself, go to the Rotating Calipers applet page .
问题
给定平面上N个点的坐标,找出距离最远的两个点。
分析
类似于“最近点对问题”,这个问题也可以用枚举的方法求解,时间复杂度O(n^2)。
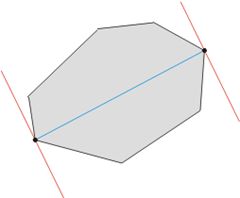
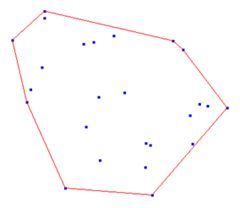
“寻找最近点对”是用到分治策略降低复杂度,而“寻找最远点对”可利用几何性质。注意到:对于平面上有n个点,这一对最远点必然存在于这n个点所构成的一个凸包上(证明略),那么可以排除大量点,如下图所示:
给定平面上N个点的坐标,找出距离最远的两个点。
分析
类似于“最近点对问题”,这个问题也可以用枚举的方法求解,时间复杂度O(n^2)。
“寻找最近点对”是用到分治策略降低复杂度,而“寻找最远点对”可利用几何性质。注意到:对于平面上有n个点,这一对最远点必然存在于这n个点所构成的一个凸包上(证明略),那么可以排除大量点,如下图所示:

在得到凸包以后,可以只在顶点上面找最远点了。同样,如果不O(n^2)两两枚举,可以想象有两条平行线, “卡”住这个凸包,然后卡紧的情况下旋转一圈,肯定就能找到凸包直径,也就找到了最远的点对。或许这就是为啥叫“旋转卡壳法”。
总结起来,问题解决步骤为:
1、用Graham's Scanning求凸包
2、用Rotating Calipers求凸包直径,也就找到了最远点对。
该算法的平均复杂度为O(nlogn) 。最坏的情况下,如果这n个点本身就构成了一个凸包,时间复杂度为O(n^2)。
旋转卡壳可以用于求凸包的直径、宽度,两个不相交凸包间的最大距离和最小距离等。虽然算法的思想不难理解,但是实现起来真的很容易让人“卡壳”。
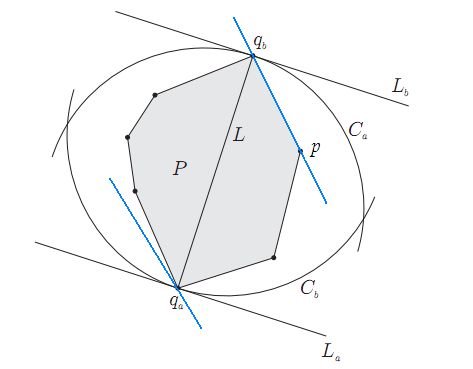
逆向思考,如果qa,qb是凸包上最远两点,必然可以分别过qa,qb画出一对平行线。通过旋转这对平行线,我们可以让它和凸包上的一条边重合,如图中蓝色直线,可以注意到,qa是凸包上离p和qb所在直线最远的点。于是我们的思路就是枚举凸包上的所有边,对每一条边找出凸包上离该边最远的顶点,计算这个顶点到该边两个端点的距离,并记录最大的值。直观上这是一个O(n2)的算法,和直接枚举任意两个顶点一样了。但是注意到当我们逆时针枚举边的时候,最远点的变化也是逆时针的,这样就可以不用从头计算最远点,而可以紧接着上一次的最远点继续计算,于是我们得到了O(n)的算法。
http://poj.org/problem?id=2187
程序:(附枚举法)
- #include <stdio.h>
- #include <algorithm>
- struct point
- {
- int x;
- int y;
- }p[50005];
- int top,stack[50005];
- inline int max(int a,int b)
- {
- return a>b?a:b;
- }
- inline int dis(const point a,const point b)
- {
- return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
- }
- inline int mult(const point p1,const point p2,const point p0)
- {
- return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
- }
- int cmp(const void *a,const void *b)
- {
- point *p1=(point*)a;
- point *p2=(point*)b;
- if(mult(*p1,*p2,p[0])<0)
- return 1;
- else if(mult(*p1,*p2,p[0])==0 && (*p1).x>(*p2).x)
- return 1;
- else return -1;
- }
- void graham(int n)
- {
- int i,min=0;
- for(i=0;i<n;i++)
- if(p[i].y<p[min].y || (p[i].y == p[min].y && p[i].x < p[min].x))
- min=i;
- point temp=p[0];
- p[0]=p[min];
- p[min]=temp;
- qsort(p+1,n-1,sizeof(point),cmp);
- stack[0]=0;
- stack[1]=1;
- stack[2]=2;
- top=2;
- for(i=3;i<n;i++)
- {
- while(top>0 && mult(p[i],p[stack[top]],p[stack[top-1]])>=0)
- top--;
- stack[++top]=i;
- }
- }
- /*int find_max()
- {
- int maxdis=0;
- for(int i=0;i<=top;i++)
- for(int j=i+1;j<=top;j++)
- if(maxdis<dis(p[stack[i]],p[stack[j]]))
- maxdis=dis(p[stack[i]],p[stack[j]]);
- return maxdis;
- }*/
- int rotating_calipers() //卡壳
- {
- int i , q=1;
- int ans = 0;
- for(i = 0 ; i < top ; i++)
- {
- while( mult( p[stack[i+1]] , p[stack[q+1]] , p[stack[i]] )
- > xmult( p[stack[i+1]] , p[stack[q]] , p[stack[i]] ) )
- q = (q+1)%(top);
- ans = max(ans , max( dis(p[stack[i]] , p[stack[q]]) , dis(p[stack[i+1]] , p[stack[q+1]])));
- }
- return ans;
- }
- int main()
- {
- int N;
- scanf("%d",&N);
- for(int i=0;i<N;i++)
- scanf("%d %d",&p[i].x,&p[i].y);
- graham(N);
- printf("%d\n",rotating_calipers()/*find_max()*/);
- return 0;
- }