第三章 -- 重建二叉树
给定一棵二叉树,假设每个节点都用唯一的字符来表示,具体结构如下:
struct NODE
{
NODE *pLeft;
NODE *pRight;
char chValue;
};
假设已经有了前序遍历和中序遍历的结果,希望通过一个算法重建这棵树。
给定函数的定义如下:
void Rebuild(char *pPreOrder, char *pInOrder, int nTreeLen, NODE **pRoot)
参数:
pPreOrder:以null为结尾的前序遍历结果的字符串数组。
pInOrder:以null为结尾的中序遍历结果的字符串数组。
nTreeLen:树的长度。
pRoot:返回node**类型,根据前序和中序遍历结果重新构建树的根节点。
例如:
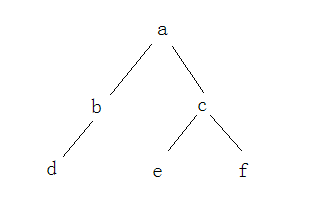
前序遍历结果:a b d c e f
中序遍历结果:d b a e c f
重建的树如图:
递归解决问题:
#include <iostream>
#define TREELEN 6
using namespace std;
struct NODE
{
NODE *lchild;
NODE *rchild;
char chValue;
};
void Rebuild(char *pPreOrder, char *pInOrder, int nTreeLen, NODE **pRoot)
{
if(pPreOrder==NULL || pInOrder==NULL)
return;
// 获得前序遍历的第一个节点
NODE *pTemp=new NODE;
pTemp->chValue=*pPreOrder;
pTemp->lchild=NULL;
pTemp->rchild=NULL;
if(*pRoot==NULL)
*pRoot=pTemp;
if(nTreeLen==1)
return;
// 开始解析字符串
char *p1=pInOrder;
char *p2=pInOrder;
//int len=0;
while(*p1!=*pPreOrder)
p1++;
//len=p1-p2;
int leftlen=(int)(p1-p2); // 左子树长度
int rightlen=nTreeLen-leftlen-1; // 右子树长度
// 重建左子树
if(leftlen>0)
//Rebuild(pPreOrder+1, pInOrder, leftlen, &(*pRoot->lchild)); ->优先级大于*
Rebuild(pPreOrder+1, pInOrder, leftlen, &((*pRoot)->lchild));
// 重建右子树
if(rightlen>0)
//Rebuild(pPreOrder+len+1, pInOrder+len+1, rightlen, &(*pRoot->rchild));
Rebuild(pPreOrder+leftlen+1, pInOrder+leftlen+1, rightlen, &((*pRoot)->rchild));
}
int PostOrderTraverse(NODE *root)
{
if(root==NULL)
return 0;
PostOrderTraverse(root->lchild);
PostOrderTraverse(root->rchild);
cout<<root->chValue<<endl;
}
int main()
{
char szPreOrder[TREELEN]={'a','b','d','c','e','f'};
char szInOrder[TREELEN]={'d','b','a','e','c','f'};
NODE *pRoot=NULL;
Rebuild(szPreOrder, szInOrder, TREELEN, &pRoot);
// 后序遍历测试
PostOrderTraverse(pRoot);
return 0;
}
测试用例结果: