划分算法与TopK问题
1 划分算法思想
划分(partition)就是将数据项分成两组,一组大于某个特定的数据项,而另一组小于某个特定的数据项。在划分算法中,这个特定的数据项叫做枢纽(pivot)。
划分算法的思想是中间线代表枢纽;数据项的左端和右端分别有两个指针(leftPtr和rightPtr); leftPtr从左向右遍历元素,rightPtr从右向左遍历元素,当leftPtr遇到比枢纽元素大的元素时停止,当rightPtr遇到比枢纽元素小的元素时停止,然后将这两个元素交换位置;接下来,leftPtr继续向右遍历,rightPtr继续向左遍历,重复上面的操作;当两个指针相遇时遍历结束。
2 代码实现
//返回划分后pivot的位置pivotIndex,位于pivotIndex左边的数字小于pivot,右边的大于pivot
public static int partionIt(int[] a,int left, int right, long pivot) {
int leftPtr=left-1;
int rightPtr=right+1;
while(true)
{
//from left to pivot
while(leftPtr<right && a[++leftPtr]<pivot);
//from right to pivot
while(rightPtr>left && a[--rightPtr]>pivot);
//base case
if(leftPtr>=rightPtr)
break;
//swap
else
swap(a,leftPtr,rightPtr);
}
return leftPtr;
}
private static void swap(int[] a,int left, int right)
{
int temp=a[right];
a[left]=a[right];
a[right]=temp;
} //end swap()
} //end partionIt
3 时间复杂度
算法时间复杂度O(N)。当在划分的2端有相同的数据需要比较和交换时,比较和交换各位N/2次,所以划分算法的时间复杂度为O(N)
4 讨论
4.1 为什么循环while(leftPtr<right && a[++leftPtr]<pivot)中要有leftPtr<right这个条件?如果数组中所有元素都小于枢纽pivot的值,那么leftPtr就会从左向右遍历元素,直到右边界的右边(当leftPtr到了数组最右边时(即leftPtr==a.length-1),那么进入下一次循环a[++leftPtr]<pivot,此时++leftPtr=a.length,数组越界了!),这样会造成数组越界,所以要有leftPtr<right来检查是否到了数组边界。同样的道理while(rightPtr>left && a[--rightPtr]>pivot)也要有rightPtr>left来检查是否数组越界。
4.2 Delicate Code
The code in the while loops is rather delicate. For example, you might be tempted to remove the increment operators from the inner while loops and use them to replace the nop statements. (Nop refers to a statement consisting only of a semicolon, and means no operation). For example, you might try to change this:
while(leftPtr < right && theArray[++leftPtr] < pivot); // (nop)
to this:
while(leftPtr < right && theArray[leftPtr] < pivot)
++leftPtr;
and similarly for the other inner while loop. These changes would make it possible for the initial values of the pointers to be left and right, which is somewhat clearer than left-1 and right+1. However, these changes result in the pointers being incremented only when the condition is satisfied. The pointers must move in any case, so two extra statements within the outer while loop would be required to bump the pointers. The nop version is the most efficient solution.(from《Data Structure and Algrithem in Java》)
4.3为什么循环while(leftPtr<right && a[++leftPtr]<pivot)中不是a[++leftPtr]<=pivot?
If you run the partitionIt() method on items that are all equal to the pivot value, you will find that every comparison leads to a swap. Swapping items with equal keys seems like a waste of time. The < and > operators that compare pivot with the array elements in the while loops cause the extra swapping. However, suppose you try to fix this by replacing them with <= and >= operators. This indeed prevents the swapping of equal elements, but it also causes leftPtr and rightPtr to end up at the ends of the array when the algorithm has finished. As we’ll see in the section on quicksort, it’s good for the pointers to end up in the middle of the array, and very bad for them to end up at the ends. So if partitionIt() is going to be used for quicksort, the < and > operators are the right way to go, even if they cause some unnecessary swapping.(from《Data Structure and Algrithem in Java》)
4.2 划分算法应用
4.2.1 划分算法在排序中的应用
划分算法是快速排序的基础,在快速排序中关键是选择划分算法中的枢纽,选择的枢纽尽可能使划分后的2个分支(左分支和右分支)概率均等,即平均切分。划分结束的条件是只有一个元素(即left==right),此时不需要划分了。
实现快速排序算法的关键在于先在数组中选择一个数字,接下来用划分算法把数组中的数字分为两部分,下面的例子选择了数组的最后一个元素作为划分枢纽。
portionIt(a,0,a.length-1, a[a.length-1])
4.2.2 求TopK问题
找出最小的K个数(或最大)。
方法一:运用划分算法,时间复杂度是O(n)
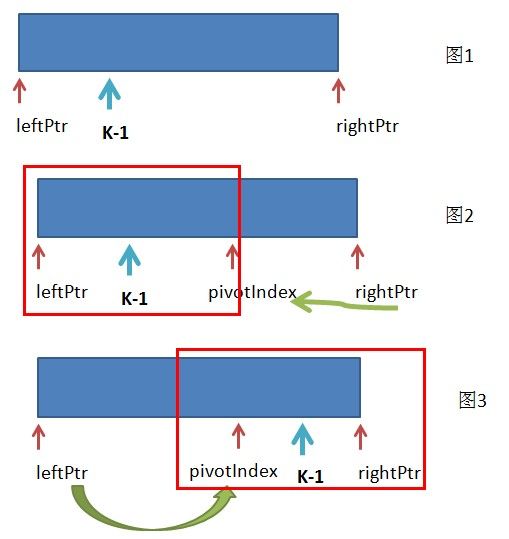
如图1第K个数的位置(最大K个数的位置为length-K),
运用划分算法,划分结束条件是划分位置pivotIndex==k-1,那么pivotIndex左边的数都小于右边的数。
运用一次划分后,pivotIndex和k-1的位置关系有3种:
1)pivotIndex==k-1,则结束
2)pivotIndex>k-1(图2),则在左区间[leftPtr,pivotIndex-1]范围运用划分算法
3)pivotIndex<k-1(图3),则在右区间[pivotIndex+1,rightPtr]范围运用划分算法
如此循环,直到pivotIndex==k-1
public void getLeastNumbers(int[] a,int k){
//输入控制
if(a==null)
return;
n=a.length;
if(k>n || k<=0)
return;
int start=0, end=n-1;
int pivot=a[n-1];
int index=partionIt(a,start,end,pivot);
while(index!=k-1){
if(index>k-1){ //in left
end=index-1;
index=partitionIt(a,start,end,pivot);
}//end if
else{ //in right
start=index+1;
index=partionIt(a,start,end,pivot);
}//end else
}//end while
//输出
for(ine i=0;i<k;i++){
System.out.println(a[i]);
}//end for
}//end getLeastNumbers()
2)方法二:运用优先队列,特别适合于处理海量问题,时间复杂度是O(nlogK)
维护一个K大小的优先队列(可以得到最大值),每次拿剩下的数与优先队列中中的最大值比较。
如果剩余数大于该最大值,则替换,否则不替换。
又如面试题:求数组中出现次数超过一半的数
假设数字出现次数超过一半,则可以转换为求第k=n/2大的数,因为第n/2大的数肯定是出现次数超过一半的数(统计学中的中位数)。
注意写代码时最后需要判断求出的数是否在数组中出现次数超过了一半(因为输入的数组可能不符合要求,即根本没有出现次数超过一半的数)。
4.2.3 数字在排序中出现的次数
题目:统计一个数字在排序数组中出现的次数。例如在排序数组中,找出给定数字的出现次数,比如 [1, 2, 2, 2, 3] 中2的出现次数是3次 。