ZOJ 2630 Plane Partition(轮廓线 状态压缩DP)

题意：

给你一个a*b的矩阵，往里面填充非负整数且满足

x(i, j) <= x(i-1, j)

x(i, j) <= x(i, j-1)

问最大的数字不超过c的填充方式有多少种。 0 < a, b, c <= 6

解题思路：

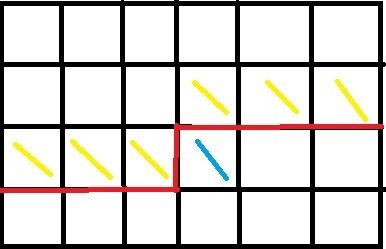
构造一个像插头DP那样的轮廓线，逐格递推DP。如下图

红色的就是轮廓线，蓝色斜线的格子就是当前决策的格子，轮廓线以上的填充数字都已经确定了，而对轮廓线一下的数字的选择填充有影响的只有轮廓线以上的黄色斜线的格子，所以有这样的DP，

dp[ x ][ y ][ zt ] 表示从格子x，y开始填充数字且轮廓线以上所有数字的压缩状态为zt的填充方式数。

我是直接把x, y, zt (轮廓线上每个格子的的数字)压缩成一个7进制的数，复杂度为 O (7^8) ，需要打表输出。

#include <stdio.h>
#include <string.h>
typedef long long ll;

const int maxn = 6000000;

ll dp[maxn];
int a, b, c, q[11];
ll ww[11][11][11];

int get(int x, int y, int q[]) {
    int ret = x;
    ret = ret*7 + y;
    for(int i = 0;i < b; i++)
        ret = ret*7 + q[i];
    return ret;
}

ll dfs(int zt) {
    int prezt = zt;
    for(int i = b-1;i >= 0; i--) {
        q[i] = zt % 7;
        zt /= 7;
    }
    int x, y;
    y = zt % 7;
    x = zt / 7;
    if(y == b) {
        x++;
        y = 0;
        return dfs( get(x, y, q) );
    }
    if(x == a)
        return 1;

    if(dp[prezt] != -1) return dp[prezt];
    int tmp = q[y];
    if(y > 0 && tmp > q[y-1])   tmp = q[y-1];
    ll ret = 0;
    int ss[11];
    for(int i = 0;i < b; i++)
        ss[i] = q[i];
    for(int i = tmp;i >= 0; i--) {
        ss[y] = i;
        ret += dfs( get(x, y+1, ss) );
    }

    return dp[prezt] = ret;
}

void init() {
ww[1][1][1] = (ll)2;
ww[1][1][2] = (ll)3;
ww[1][1][3] = (ll)4;
ww[1][1][4] = (ll)5;
ww[1][1][5] = (ll)6;
ww[1][1][6] = (ll)7;
ww[1][2][1] = (ll)3;
ww[1][2][2] = (ll)6;
ww[1][2][3] = (ll)10;
ww[1][2][4] = (ll)15;
ww[1][2][5] = (ll)21;
ww[1][2][6] = (ll)28;
ww[1][3][1] = (ll)4;
ww[1][3][2] = (ll)10;
ww[1][3][3] = (ll)20;
ww[1][3][4] = (ll)35;
ww[1][3][5] = (ll)56;
ww[1][3][6] = (ll)84;
ww[1][4][1] = (ll)5;
ww[1][4][2] = (ll)15;
ww[1][4][3] = (ll)35;
ww[1][4][4] = (ll)70;
ww[1][4][5] = (ll)126;
ww[1][4][6] = (ll)210;
ww[1][5][1] = (ll)6;
ww[1][5][2] = (ll)21;
ww[1][5][3] = (ll)56;
ww[1][5][4] = (ll)126;
ww[1][5][5] = (ll)252;
ww[1][5][6] = (ll)462;
ww[1][6][1] = (ll)7;
ww[1][6][2] = (ll)28;
ww[1][6][3] = (ll)84;
ww[1][6][4] = (ll)210;
ww[1][6][5] = (ll)462;
ww[1][6][6] = (ll)924;
ww[2][1][1] = (ll)3;
ww[2][1][2] = (ll)6;
ww[2][1][3] = (ll)10;
ww[2][1][4] = (ll)15;
ww[2][1][5] = (ll)21;
ww[2][1][6] = (ll)28;
ww[2][2][1] = (ll)6;
ww[2][2][2] = (ll)20;
ww[2][2][3] = (ll)50;
ww[2][2][4] = (ll)105;
ww[2][2][5] = (ll)196;
ww[2][2][6] = (ll)336;
ww[2][3][1] = (ll)10;
ww[2][3][2] = (ll)50;
ww[2][3][3] = (ll)175;
ww[2][3][4] = (ll)490;
ww[2][3][5] = (ll)1176;
ww[2][3][6] = (ll)2520;
ww[2][4][1] = (ll)15;
ww[2][4][2] = (ll)105;
ww[2][4][3] = (ll)490;
ww[2][4][4] = (ll)1764;
ww[2][4][5] = (ll)5292;
ww[2][4][6] = (ll)13860;
ww[2][5][1] = (ll)21;
ww[2][5][2] = (ll)196;
ww[2][5][3] = (ll)1176;
ww[2][5][4] = (ll)5292;
ww[2][5][5] = (ll)19404;
ww[2][5][6] = (ll)60984;
ww[2][6][1] = (ll)28;
ww[2][6][2] = (ll)336;
ww[2][6][3] = (ll)2520;
ww[2][6][4] = (ll)13860;
ww[2][6][5] = (ll)60984;
ww[2][6][6] = (ll)226512;
ww[3][1][1] = (ll)4;
ww[3][1][2] = (ll)10;
ww[3][1][3] = (ll)20;
ww[3][1][4] = (ll)35;
ww[3][1][5] = (ll)56;
ww[3][1][6] = (ll)84;
ww[3][2][1] = (ll)10;
ww[3][2][2] = (ll)50;
ww[3][2][3] = (ll)175;
ww[3][2][4] = (ll)490;
ww[3][2][5] = (ll)1176;
ww[3][2][6] = (ll)2520;
ww[3][3][1] = (ll)20;
ww[3][3][2] = (ll)175;
ww[3][3][3] = (ll)980;
ww[3][3][4] = (ll)4116;
ww[3][3][5] = (ll)14112;
ww[3][3][6] = (ll)41580;
ww[3][4][1] = (ll)35;
ww[3][4][2] = (ll)490;
ww[3][4][3] = (ll)4116;
ww[3][4][4] = (ll)24696;
ww[3][4][5] = (ll)116424;
ww[3][4][6] = (ll)457380;
ww[3][5][1] = (ll)56;
ww[3][5][2] = (ll)1176;
ww[3][5][3] = (ll)14112;
ww[3][5][4] = (ll)116424;
ww[3][5][5] = (ll)731808;
ww[3][5][6] = (ll)3737448;
ww[3][6][1] = (ll)84;
ww[3][6][2] = (ll)2520;
ww[3][6][3] = (ll)41580;
ww[3][6][4] = (ll)457380;
ww[3][6][5] = (ll)3737448;
ww[3][6][6] = (ll)24293412;
ww[4][1][1] = (ll)5;
ww[4][1][2] = (ll)15;
ww[4][1][3] = (ll)35;
ww[4][1][4] = (ll)70;
ww[4][1][5] = (ll)126;
ww[4][1][6] = (ll)210;
ww[4][2][1] = (ll)15;
ww[4][2][2] = (ll)105;
ww[4][2][3] = (ll)490;
ww[4][2][4] = (ll)1764;
ww[4][2][5] = (ll)5292;
ww[4][2][6] = (ll)13860;
ww[4][3][1] = (ll)35;
ww[4][3][2] = (ll)490;
ww[4][3][3] = (ll)4116;
ww[4][3][4] = (ll)24696;
ww[4][3][5] = (ll)116424;
ww[4][3][6] = (ll)457380;
ww[4][4][1] = (ll)70;
ww[4][4][2] = (ll)1764;
ww[4][4][3] = (ll)24696;
ww[4][4][4] = (ll)232848;
ww[4][4][5] = (ll)1646568;
ww[4][4][6] = (ll)9343620;
ww[4][5][1] = (ll)126;
ww[4][5][2] = (ll)5292;
ww[4][5][3] = (ll)116424;
ww[4][5][4] = (ll)1646568;
ww[4][5][5] = (ll)16818516;
ww[4][5][6] = (ll)133613766;
ww[4][6][1] = (ll)210;
ww[4][6][2] = (ll)13860;
ww[4][6][3] = (ll)457380;
ww[4][6][4] = (ll)9343620;
ww[4][6][5] = (ll)133613766;
ww[4][6][6] = (ll)1447482465;
ww[5][1][1] = (ll)6;
ww[5][1][2] = (ll)21;
ww[5][1][3] = (ll)56;
ww[5][1][4] = (ll)126;
ww[5][1][5] = (ll)252;
ww[5][1][6] = (ll)462;
ww[5][2][1] = (ll)21;
ww[5][2][2] = (ll)196;
ww[5][2][3] = (ll)1176;
ww[5][2][4] = (ll)5292;
ww[5][2][5] = (ll)19404;
ww[5][2][6] = (ll)60984;
ww[5][3][1] = (ll)56;
ww[5][3][2] = (ll)1176;
ww[5][3][3] = (ll)14112;
ww[5][3][4] = (ll)116424;
ww[5][3][5] = (ll)731808;
ww[5][3][6] = (ll)3737448;
ww[5][4][1] = (ll)126;
ww[5][4][2] = (ll)5292;
ww[5][4][3] = (ll)116424;
ww[5][4][4] = (ll)1646568;
ww[5][4][5] = (ll)16818516;
ww[5][4][6] = (ll)133613766;
ww[5][5][1] = (ll)252;
ww[5][5][2] = (ll)19404;
ww[5][5][3] = (ll)731808;
ww[5][5][4] = (ll)16818516;
ww[5][5][5] = (ll)267227532;
ww[5][5][6] = (ll)3184461423;
ww[5][6][1] = (ll)462;
ww[5][6][2] = (ll)60984;
ww[5][6][3] = (ll)3737448;
ww[5][6][4] = (ll)133613766;
ww[5][6][5] = (ll)3184461423;
ww[5][6][6] = (ll)55197331332;
ww[6][1][1] = (ll)7;
ww[6][1][2] = (ll)28;
ww[6][1][3] = (ll)84;
ww[6][1][4] = (ll)210;
ww[6][1][5] = (ll)462;
ww[6][1][6] = (ll)924;
ww[6][2][1] = (ll)28;
ww[6][2][2] = (ll)336;
ww[6][2][3] = (ll)2520;
ww[6][2][4] = (ll)13860;
ww[6][2][5] = (ll)60984;
ww[6][2][6] = (ll)226512;
ww[6][3][1] = (ll)84;
ww[6][3][2] = (ll)2520;
ww[6][3][3] = (ll)41580;
ww[6][3][4] = (ll)457380;
ww[6][3][5] = (ll)3737448;
ww[6][3][6] = (ll)24293412;
ww[6][4][1] = (ll)210;
ww[6][4][2] = (ll)13860;
ww[6][4][3] = (ll)457380;
ww[6][4][4] = (ll)9343620;
ww[6][4][5] = (ll)133613766;
ww[6][4][6] = (ll)1447482465;
ww[6][5][1] = (ll)462;
ww[6][5][2] = (ll)60984;
ww[6][5][3] = (ll)3737448;
ww[6][5][4] = (ll)133613766;
ww[6][5][5] = (ll)3184461423;
ww[6][5][6] = (ll)55197331332;
ww[6][6][1] = (ll)924;
ww[6][6][2] = (ll)226512;
ww[6][6][3] = (ll)24293412;
ww[6][6][4] = (ll)1447482465;
ww[6][6][5] = (ll)55197331332;
ww[6][6][6] = (ll)1478619421136;
}

int main() {

/*
    for(int i = 1;i <= 6; i++) {
        for(int j = 1;j <= 6; j++) {
            for(int k = 1;k <= 6; k++) {
                a = i; b = j; c = k;
                memset(dp, -1, sizeof(dp));
                for(int l = 0;l < b; l++) {
                    q[l] = c;
                }
                ww[i][j][k] = dfs( get(0, 0, q) );
            }
        }
    }
    for(int i = 1;i <= 6; i++) {
        for(int j = 1;j <= 6; j++) {
            for(int k = 1;k <= 6; k++) {
                printf("ww[%d][%d][%d] = (ll)%I64d;\n", i, j, k, ww[i][j][k]);
            }
        }
    }
*/
    init();
    while(scanf("%d%d%d", &a, &b, &c) != -1) {
        printf("%lld\n", ww[a][b][c]);
    }

    return 0;
}