Spoj 375 Qtree 树链剖分 + 线段树 解法
前面介绍过Qtree的动态树解法,现在写一种更高效的,使用树链剖分,数据结构采用线段树:
题目链接:http://www.spoj.pl/problems/QTREE/
代码:
#include <stdio.h>
#include <string.h>
#include <queue>
#include <vector>
using namespace std;
#define MAXN 10010
#define lx (x<<1)
#define rx (x<<1 | 1)
#define MID ((l + r)>>1)
int A[MAXN];//存储边长
int M[MAXN<<2];//建立线段树
int T;
int N;
int static_id;
struct ANode
{
int v;
int w;
ANode * next;
ANode(int _v,int _w,ANode * _next)
{
v = _v;
w = _w;
next = _next;
}
}*adj[MAXN];
struct Node
{
Node * father;
Node * ch;
int cost;
int deep;
bool vis;
int size;
int top;
int tid;
int id;
} tree[MAXN],*null,Tnull;
vector<pair<int,int> > edge;
void init(Node * p)
{
p->father = p->ch = null;
p->vis = false;
}
//生成重链
void dfs(int x,int father,int depth)
{
tree[x].deep = depth;
if(father!=0)
{
tree[x].father = tree + father;
}
tree[x].size = 1;
tree[x].vis = true;
int maxsize = 0;
for(ANode * p = adj[x]; p; p=p->next)
{
if(tree[p->v].vis == false)
{
dfs(p->v,x,depth+1);
tree[p->v].cost = p->w;
tree[x].size += tree[p->v].size;
if(tree[p->v].size > maxsize)
{
maxsize = tree[p->v].size;
tree[x].ch = tree + p->v;
}
}
}
}
//连接重链
void dfs2(int x,int ancestor)
{
tree[x].vis = true;
tree[x].tid = ++static_id;
tree[x].top = ancestor;
if(tree[x].ch!=null)
{
dfs2(tree[x].ch->id,ancestor);
}
for(ANode * p = adj[x]; p; p = p->next)
{
if(tree[p->v].vis == false)
{
dfs2(tree[p->v].id,tree[p->v].id);
}
}
}
void build(int l,int r,int x)
{
if(l == r)
{
M[x] = A[l];
return;
}
build(l,MID,lx);
build(MID+1,r,rx);
M[x] = max(M[lx],M[rx]);
}
//在线段树中查找,返回某一个区间内的最大值
int query2(int l,int r,int x,int L,int R)
{
if(L<=l && R>=r)
{
return M[x];
}
int temp = 0;
if(L<= MID)
{
temp = max(temp,query2(l,MID,lx,L,R));
}
//注意千万不要加else ,否则会WA
if(R > MID)
{
temp = max(temp,query2(MID+1,r,rx,L,R));
}
return temp;
}
//在原有树中查找,返回两个节点中的最大值
int query(int a,int b)
{
int ans = 0;
while(tree[a].top != tree[b].top)
{
if(tree[tree[a].top].deep < tree[tree[b].top].deep)
{
swap(a,b);
}
ans = max(ans,query2(2,N,1,tree[tree[a].top].tid,tree[a].tid));
a = tree[tree[a].top].father->id;
}
if(tree[a].deep > tree[b].deep)
{
swap(a,b);
}
if(a!=b)
{
ans = max(ans,query2(2,N,1,tree[a].tid + 1,tree[b].tid));
}
return ans;
}
void update(int l,int r,int x,int p,int c)
{
if(l == r)
{
M[x] = c;
return;
}
if(p<=MID)
{
update(l,MID,lx,p,c);
}
else
{
update(MID+1,r,rx,p,c);
}
M[x] = max(M[lx],M[rx]);
}
void change(int a,int b)
{
if(tree[edge[a].first].deep > tree[edge[a].second].deep)
{
update(2,N,1,tree[edge[a].first].tid,b);
}
else
{
update(2,N,1,tree[edge[a].second].tid,b);
}
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
#endif
int a,b,c;
char cmd[20];
scanf("%d",&T);
null = &Tnull;
init(null);
null->id = -1;
while(T--)
{
scanf("%d",&N);
static_id = 0;
memset(A,0,sizeof(A));
memset(M,0,sizeof(M));
for(int i=1; i<=N; i++)
{
adj[i] = NULL;
init(&tree[i]);
tree[i].id = i;
}
edge.clear();
for(int i=0; i<N-1; i++)
{
scanf("%d%d%d",&a,&b,&c);
adj[a] = new ANode(b,c,adj[a]);
adj[b] = new ANode(a,c,adj[b]);
edge.push_back(make_pair(a,b));
}
dfs(1,0,1);
for(int i=1; i<=N; i++)
{
tree[i].vis = false;
}
dfs2(1,1);
for(int i = 0; i<N-1; i++)
{
if(tree[edge[i].first].deep > tree[edge[i].second].deep)
{
A[tree[edge[i].first].tid] = tree[edge[i].first].cost;
}
else
{
A[tree[edge[i].second].tid] = tree[edge[i].second].cost;
}
}
build(2,N,1);//对数组A build 线段树
while(1)
{
scanf("%s",cmd);
if(strcmp(cmd,"QUERY") == 0)
{
scanf("%d%d",&a,&b);
printf("%d\n",query(a,b));
}
if(strcmp(cmd,"CHANGE") == 0)
{
scanf("%d%d",&a,&b);
a--;
change(a,b);
}
if(strcmp(cmd,"DONE")==0)
{
break;
}
}
}
return 0;
}
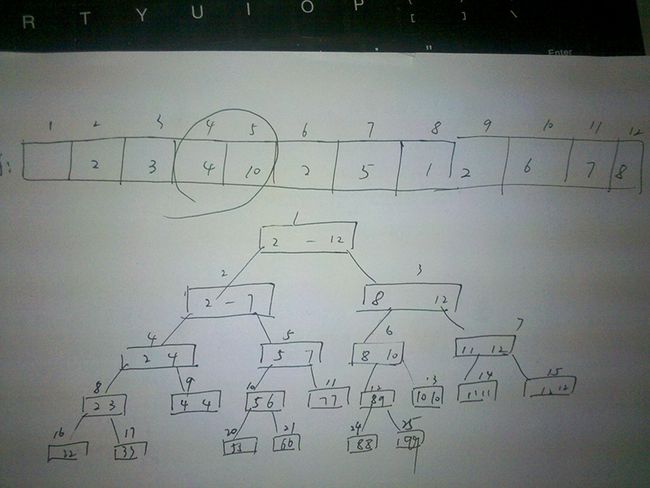
对于query2这个函数,及,查询某一区间的最值,切忌不要加else,也就是说要双向比较:
理由如图:
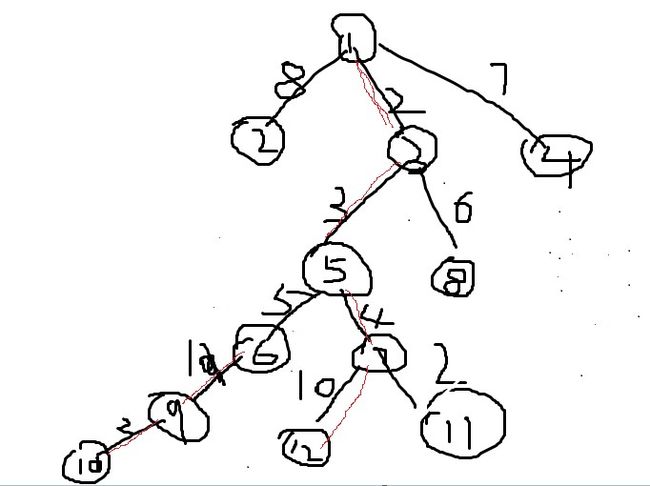
比如对于Qtree我有这样一组数据:
1 12 2 1 8 3 1 2 4 1 7 3 5 3 8 3 6 5 6 5 5 7 4 9 6 1 10 9 2 7 11 2 7 12 10 QUERY 5 12 DONE
那么,QUERY 5 12 应该是第 4 、5条边的极大值,
如果我这样写:
if(L<= MID)
{
temp = max(temp,query2(l,MID,lx,L,R));
}
//注意千万不要加else ,否则会WA
else if(R > MID)
{
temp = max(temp,query2(MID+1,r,rx,L,R));
}就会出错。理由:
4,5跨两个区间。