vijos - P1279Leave-绿光(数学归纳法 + python)

P1279Leave-绿光

Accepted

标签： [显示标签]

背景

期待这一份幸运，和一份冲劲，多么奇妙的际遇……。燕姿在演唱完绿光这首歌后，出给了姿迷一个考题。

北欧有一个传说！
人一生中能看见绿光！
他就一生都可以得到幸福！

描述

燕姿唱完这首歌，天上降落了一道绿光，在地上形成了一个矩形的映射，矩形的长为a，宽为b。燕姿向姿迷出了一个考题，谁能够把这个矩形绿光阵分成若干个正整数的正方形，谁的正方形边长之和最小，他就将得到燕姿的一个合影。姿迷们都很想得到合影，可是怎么分才最小呢？大家都束手无策，现在，这个问题交给你了。

歌迷X：呜呜呜，俺的语文不好，听不懂你在讲什么。

燕姿：别怕，其实这个问题可以简化为……

将边长为正整数a，b的长方形划分成若干边长均为正整数，每个正方形的边均平行于矩形的相应边，试求这些正方形边之和的最小值MIN。

(如果这个长方形可以分成N个正方形，其中每个边长为Ai,那么MIN=A1+A2+^^^+AN
注意，数组A中的元素可能相等）

格式

输入格式

一共10行
每行两个正整数，Ai，Bi

对于30%的数据，Ai，Bi<maxint
对于100%的数据，Ai，Bi<maxlongint;

输出格式

一共10行
每行一个整数，输出MINi

样例1

样例输入1[复制]

1 1
2 1
3 1
4 1
5 1
6 1
7 1
8 1
9 1
10 1

样例输出1[复制]

1
2
3
4
5
6
7
8
9
10

限制

每点1s

提示

对于样例，可全分长边长为一的正方形，并

记所求最小值为f(m,n),可以证明f(m,n)=m+n-(m,n). (*)
其中(m,n)表示m和n的最大公约数.
事实上,不妨设m≥n.
(1)关于m归纳,可以证明存在一种合乎题意的分法,使所得正方形边长之和恰为m+n-(m,n).
当m=1时,命题显然成立. 
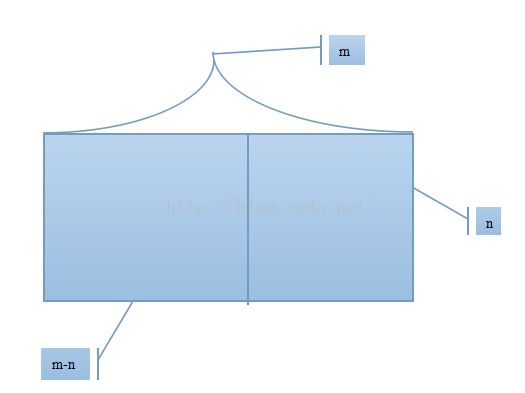
假设当m≤k时,结论成立(k≥1).当m=k+1时,若n= k+1,则命题显然成立.若n< k+1,从矩形ABCD中切去正方形一个边长为n(如图),

由归纳假设剩下的矩形有一种分法使得所得正方形边长之和恰为m-n+n-(m-n,n)= m-(m,n).
于是原矩形ABCD有一种分法使得所得正方形边长之和为m+n- (m,n).
(2)关于m归纳可以证明(*)成立.
当m=1时,由于n=1,显然f (m,n)=1= m+n- (m,n).
假设当m≤k时,对任意1≤n≤m有f (m,n)= m+n- (m,n).
若m=k+1,当n= k+1时,显然f(m,n)= k+1= m+n- (m,n).
当1≤n≤k时,设矩形ABCD按要求分成了p个正方形,其边长分别为a1,a2,…,ap,不妨设a1≥a2≥…≥ap.
显然a1=n或a1若a1 m+n- (m,n).
若a1=n,则一个边长分别为m-n和n的矩形可按题目要求分成边长分别为a2,…,ap的正方形,由归纳假设
a2+…+ap≥m-n+n-(m-n,n)= m- (m,n).
从而a1+a2+…+ap≥m+n-(m,n).
于是当m=k+1时,f(m,n)≥m+n- (m,n).
再由(1)可知f (m,n)=m+n- (m,n).

#!/usr/bin/env python3
# -*- coding: utf-8 -*-


def gcd(a, b):
    if not b:
        return a
    else :
        return gcd(b, a % b)
def lcm(a, b):
    return a + b - gcd(a, b)
import sys
import math
for i in range(10):
    a, b = map(int,raw_input().split())
    print lcm(a, b)