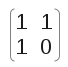HDOJ 1588 - Gauss Fibonacci
Matrix Multiplication (& Quick Power)
Description
g(x) = k * x + b。
f(x) 为Fibonacci数列。
求f(g(x)),从x = 1到n的数字之和,并对m取模。
Type
Matrix Multiplication
Quick Power
Analysis
我们知道f(x)中,两个元素之间的关系是
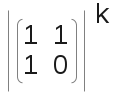
因为g(x) – b,为一个等比数列,所以,他们之间也有一个类似Fibonacci的关系,并且可以用矩阵来表示
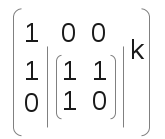
而为了求和,我们可以添加一项s(x),用来表示前x项的和,最后得到矩阵
( s(x-1),f(g(x)),f(g(x)-1) ) = ( s(x – 2), f(g(x – 1), f(g(x – 1) – 1)) ) ×
剩下的工作就是矩阵乘法和快速幂了。
Solution
// HDOJ 1588
// Gauss Fibonacci
// by A Code Rabbit
#include <cstdio>
#include <cstring>
const int MAXO = 5;
template <typename T>
struct Matrix {
T e[MAXO][MAXO];
int o;
Matrix(int order) { memset(e, 0, sizeof(e)); o = order; }
Matrix operator*(const Matrix& one) {
Matrix res(o);
for (int i = 0; i < o; i++)
for (int j = 0; j < o; j++)
for (int k = 0; k < o; k++)
res.e[i][j] += e[i][k] * one.e[k][j];
return res;
}
Matrix operator%(int mod) {
for (int i = 0; i < o; i++)
for (int j = 0; j < o; j++)
e[i][j] %= mod;
return *this;
}
};
template <typename T>
T QuickPower(T radix, int exp, int mod) {
T res = radix;
exp--;
while (exp) {
if (exp & 1) res = res * radix % mod;
exp >>= 1;
radix = radix * radix % mod;
}
return res;
}
int k, b, n, m;
int Fibonacci(int x);
int main() {
while (scanf("%d%d%d%d", &k, &b, &n, &m) != EOF) {
// Initialize in the first time.
Matrix<long long> mat_one1(2);
mat_one1.e[0][0] = 1;
mat_one1.e[0][1] = 1;
mat_one1.e[1][0] = 1;
// Quick power for computing the matrix of the relation of two nest
// pair of numbers in g(x).
Matrix<long long> mat_ans1 = QuickPower(mat_one1, k, m);
// Initialize in the second time.
Matrix<long long> mat_one2(3);
mat_one2.e[0][0] = 1;
mat_one2.e[1][0] = 1;
for (int i = 1; i < 3; ++i)
for (int j = 1; j < 3; ++j)
mat_one2.e[i][j] = mat_ans1.e[i - 1][j - 1];
// Quick power for computing the sum of g(x).
Matrix<long long> mat_ans2 = QuickPower(mat_one2, n - 1, m);
// Output.
int original_solution[] = {
Fibonacci(b),
Fibonacci(k + b),
Fibonacci(k + b - 1),
};
long long sum = 0;
for (int i = 0; i < 3; i++)
sum += original_solution[i] * mat_ans2.e[i][0];
printf("%lld\n", sum % m);
}
return 0;
}
int Fibonacci(int x) {
if (!x) return 0;
Matrix<long long> mat_one(2);
// Initialize mat_one.
mat_one.e[0][0] = 1;
mat_one.e[0][1] = 1;
mat_one.e[1][0] = 1;
// Quick power.
Matrix<long long> mat_ans = QuickPower(mat_one, x, m);
// Compete and return the result.
return mat_ans.e[1][0];
}