poj - 2528 - Mayor's posters（线段树（区间更新））

题意：一条固定高度与宽度的长长的（10000000）展栏，n（1 <= n <= 10000）上候选人要贴n张海报到栏上，每张海报高度与展栏高度一样，但长度不定，按顺序先后贴上n张海报，输入各张海报的左端值与右端值[l, r]，表示将海报贴在此区间，问最后总共能看见多少张海报？（看到就行，不用看全）

题目链接：http://poj.org/problem?id=2528

——>>离散化线段树来做，却不想离散化写了大半天……

        原来的：1  2  3  4  6  7  8  10

        映射后：1  2  3  4  5  6  7  8

        原来的：[1, 4]   [2, 6]   [8, 10]   [3, 4]   [7, 10]

        映射后：[1, 4]   [2, 5]   [7, 8]     [3, 4]   [6, 8]

——>>怎么映射法呢？（几个月前，周师兄告诉我们用离散线段树解题，写到今天，总算会了点离散线段了……ORZ）

一条线段，有2个端点，离散时每个端点都要参与排序，那排序后怎么知道哪个点与哪个点原来属同一线段呢？方法之一是，每个端点携带一个id，同一条线段携带同一个id，但正负性不同，个人用-id表示左端点，+id表示右端点，那么，端点排序后，用一个计数器cnt，对端点进行后一个与前一个比较值是否相同就行，同的话，cnt不加，不同的话，cnt+1，最后根据id存入映射线段数组就好。

——>>然后，进行线段树区间修改，更新时，每次更新都是设一个不同的值，查询时统计setv值即可。这里用STL中的<set>来统计，因为加入set中的元素，如果相同的话，是加不进去的，最后用.size()输出——AC!

/*************************************************** ADD

有朋友指出，以下算法可以AC，但是不对。

说得对，对于这道题，真让我着了急，现在也没解决的办法……

以下程序不正确的的原因：

若有一组数据[1, 10]   [1, 3]   [6, 10]

离散化后是：[1, 4]   [1, 2]   [3, 4]

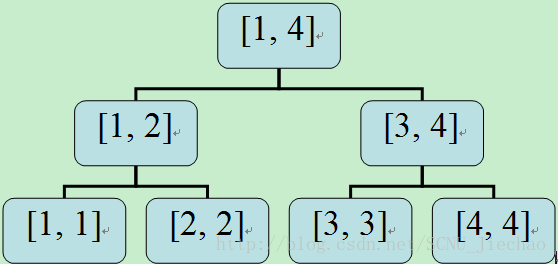
以下程序是建成的线段树是这样的：

离散化前，3与6之间是有间隙的，但是离散化后，2与3相连的，于是原来3与6之间的部分就看不到，少算了，得到的结果是2，而正解是3。

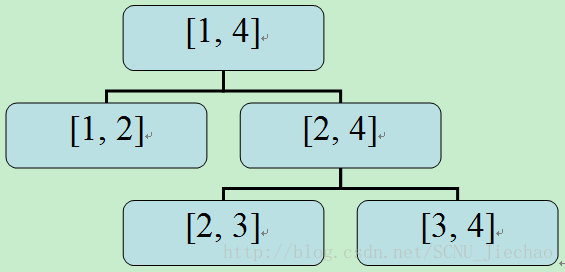
如果另外一种方式建树：

若有一组数据[5, 6]   [4, 5]   [6, 8]

离散化后是：[2, 3]   [1, 2]   [3, 4]

离散化前，后两个数据把第一个[5, 6]给覆盖了，而离散化后，三个数据独立，多计了，这种建树方式得到结果是3，而正解是2。

纠结，这题该怎么破？恳求路过的朋友指点……

#include <cstdio>
#include <algorithm>
#include <set>

using namespace std;

const int maxn = 10000 + 10;
int seg[maxn][2], setv[maxn<<2];
set<int> se;
struct Cver
{
    int num;        //原序号
    int id;     //用来标记同一条线段
    bool operator < (const Cver& v) const
    {
        return num < v.num || (num == v.num && id < v.id);
    }
}ver[maxn<<1];      //端点

void build(int o, int L, int R)     //建树
{
    if(L == R)
    {
        setv[o] = -1;       //建树目的
        return;
    }
    int M = L + (R - L) / 2;
    build(o<<1, L, M);
    build(o<<1|1, M+1, R);
    setv[o] = -1;       //建树目的
}
void pushdown(int o, int L, int R)      //下传
{
    if(setv[o] >= 0)
    {
        setv[o<<1] = setv[o];
        setv[o<<1|1] = setv[o];
        setv[o] = -1;
    }
}
void update(int o, int L, int R, int y1, int y2, int v)     //更新
{
    if(y1 <= L && R <= y2)
    {
        setv[o] = v;
        return;
    }
    pushdown(o, L, R);
    int M = L + (R - L) / 2;
    if(y1 <= M) update(o<<1, L, M, y1, y2, v);
    if(y2 > M) update(o<<1|1, M+1, R, y1, y2, v);
}
void query(int o, int L, int R, int y1, int y2)     //查询
{
    if(setv[o] >= 0)
    {
        se.insert(setv[o]);     //统计
        return;
    }
    int M = L + (R - L) / 2;
    query(o<<1, L, M, y1, y2);
    query(o<<1|1, M+1, R, y1, y2);
}
int main()
{
    int C, n, i;
    scanf("%d", &C);
    while(C--)
    {
        scanf("%d", &n);
        for(i = 1; i <= n; i++)
        {
            scanf("%d%d", &ver[(i<<1)-1].num, &ver[i<<1].num);      //原始点
            ver[(i<<1)-1].id = -i;      //-为左端
            ver[i<<1].id = i;       //+为右端
        }
        sort(ver+1, ver+1+(n<<1));
        ver[0].num = -1;
        int cnt = 0;     //cnt为计数器，靠其重新编号
        for(i = 1; i <= (n<<1); i++)        //离散化
        {
            if(ver[i].num != ver[i-1].num) cnt++;       //判断与上一个数是否相同
            if(ver[i].id < 0) seg[-ver[i].id][0] = cnt;     //重新编号（左端）
            else seg[ver[i].id][1] = cnt;       //重新编号（右端）
        }
        build(1, 1, cnt);       //建树
        for(i = 1; i <= n; i++) update(1, 1, cnt, seg[i][0], seg[i][1], i);     //更新
        query(1, 1, cnt, 1, cnt);       //查询
        printf("%d\n", se.size());
        se.clear();     //清空，避免对下一组测试数据产生影响
    }
    return 0;
}