3D游戏寻路算法(A*)
关于游戏中A*的算法优化,由于在搜索的过程中会通过open表和close保存一些结点,为了加快查找效率一般采用对维护的方式,利用map的最小堆(按照估价值的大小排序)来构架数据结构。其实还可以利用线性的hash_map来创建维护。
而3D中游戏寻路也是采用同样的方法,只是在不同于2D的8个方向搜索而是3*8个方向的搜索。所以他的复杂度之高,在对于一个3维的N*N*N的空间,他的搜索运算为n^3*24,就需要考虑算法中的优化。
总之一句3D寻路费时又费空间!
下面是我总结的优化
1.总体还是利用a*和堆维护。
2.由于点是实心,可以直接进行对角线的行走,也就是对角线行走一步后x,y,z的坐标都会改变,从而降低通过2次二维变换的过程。二步变一步!
3.利用凸包的方式来优化。
4.把一个场景的3D地图全部细分,利用多叉树进行管理。
关于凸包的优化可以通过这样一个例子说明(因为在2D中更好的描述通过2维的地图):
A、假设1要到2的,通过A*的搜索,他会先到0然后发现不能通过在回溯,重新寻找新的路径,这样可能浪费一些搜索时间。
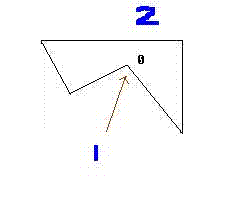
B. 可以通过多边形的最小矩形凸包的方式,这样就可以减少不必要的搜索,如图所示。

那么1到2就不会经过0点。。因为次区域设置为不可通过。
C. 如果我们要查找的点在我们凸包内,所以我们在寻路最开始应该验证点是否在凸包内,如果在此区域内,在行走时不能过滤这个矩形空间。
注:游戏中地图一般是不变的,所以这些都是不变,凸包已知,验证点在凸包中也是线性的。
由于在计算3D的凸包的时候计算量大,最开始采用静态的方式来记录数据。
简单的3D寻路算法源码(不包含凸包优化):
/Files/expter/3DAStar.rar
上文来自:http://www.cppblog.com/expter/archive/2009/10/10/98282.html
3d游戏寻路简介
A*的最初设计是基于2d平面,对于3d 寻路就需要先对场景网格化,生成平面,把3d的问题转化为2d的问题,然后就可以通过A*进行寻路。
3d 游戏寻路大致分为2部分:navmesh(3d转2d)、A*算法
网格数据(navmesh)生成:
1、Voxelization – Create a solid heightfield from the source geometry.
2、Generate Regions – Detect the top surface area of the solid heightfield and divide it up into regions of contiguous spans.
3、Generate Contours – Detect the contours of the regions and form them into simple polygons.
4、Generate Polygon Mesh – Sub-divide the contours into convex polygons.
5、Generate Detailed Mesh – Triangulate the polygon mesh and add height detail.
相关概念: 体素化Voxelization 向量空间(vector space) 到 体素空间(voxel space) 的转换. 用到的是叫保守体素化(Conservative voxelization) 的算法, 它保证了每个多边形面都能完全被生成的三维象素(voxel)包裹。
体素化后, 生成的都是可寻路的高度场(heightfield)信息, 不可寻路部分被剔除.这一步是从一个固态高度场(solid heightfield) 生成一个开放高度场(open heightfield) 的过程, 一个开放高度场表示在一个固态空间上可能寻路的平面.
区域生成Region Generation 定义,哪部分的面是可以寻路的, 并且把寻路区域分隔成连续的平面以供最后生成简单寻路多边形. 最终结果, 墙体,围栏, 柱子, 桌子底等不可能寻路的平面在这步根据邻居信息和分水岭算法(the watershed algorithm) 被剔除, 一些孤立的小局域(比如桌子表面) 也被剔除. 楼梯, 虽然是多级, 也会被当做一个平面(绿色). 楼梯扶手等平面也被剔除.
轮廓生成Contour Generation 完成从体素空间回到向量空间的转换. 区域(region) 轮廓将被"遍历(walk)", 形成简单的多边形.其中, 有些区域被合并, 多边形的边更平滑, 边长度被优化. 此时,可寻路区域已经被一些简化的多边形所表示。
凸多边形生成Convex Polygon Generation:把多边形切分为三角形, 而后尽量合并的方式 精细网格生成
Detailed Mesh Generation: 通过"德劳内三角化"(Delaunay triangulation) 算法三角化成包含高度信息的三角形,顶点信息也会在这里补到各个三角形上, 以保证高度信息和模型保持一致.
A* (a-star,A星)大致描述:
1、把起始格添加到开启列表。
2、寻找开启列表中F值最低的格子(当前格),将其切到关闭列表
3、对相邻的8格最如下处理:如果它不在开启列表中,把它加进去 ;如果它已经在开启列表中,用G值为参考检查新的路径是否更好。更低的G值意味着更好的路径。如果这样,把这一格的父节点改成当前格,并且重新计算这一格的G和F值。如果你保持你的 开启列表按F值排序,改变之后你可能需要重新对开启列表排序。
4、当把目标格添加进了关闭列表,这时候路径被找到;如果没有找到目标格,开启列表已经空了,这时候,路径不存在。 最后,保存路径,从目标格开始,沿着每一格的父节点移动直到回到起始格。这就是需要的路径。
(1-4是个循环过程)
附注:
开启/关闭列表:临时记录区,算法中的变量
G值:从起点A,沿着产生的路径,移动到网格上指定方格的移动耗费。
H值:从网格上那个方格移动到终点B的预估移动耗费。
F值:G + H 父节点:记录最短路径
A*(A-Star)算法:公式: f(n)=g(n)+h(n)
f(n) 是节点n从初始点到目标点的估价函数
g(n) 是在状态空间中从初始节点到n节点的实际代价
h(n)是从n到目标节点最佳路径的估计代价 最短路径,关键在于估价函数h(n): 估价值h(n)<= n到目标节点的距离实际值,搜索的点数多,搜索范围大,效率低。但能得到最优解。
估价值>实际值, 搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。 估价值与实际值越接近,估价函数取得就越好 对几何路网来说,取两节点间欧几理德距离(直线距离)做为估价值,即f=g(n)+sqrt((dx-nx)*(dx-nx)+(dy- ny)*(dy-ny));这样估价函数f在g值一定的情况下,会或多或少的受估价值h的制约,节点距目标点近,h值小,f值相对就小,能保证最短路的搜索向终点的方向进行。
算法的搜索过程: 创建两个表,OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。 遍历当前节点的各个节点,将n节点放入CLOSE中,取n节点的子节点X,->算X的估价值。
伪代码: While(OPEN!=NULL)
{
从OPEN表中取估价值f最小的节点n;
if(n节点==目标节点)
break;
else
{
if(X in OPEN) 比较两个X的估价值f //注意是同一个节点的两个不同路径的估价值 if( X的估价值小于OPEN表的估价值 ) 更新OPEN表中的估价值; //取最小路径的估价值
if(X in CLOSE) 比较两个X的估价值 //注意是同一个节点的两个不同路径的估价值 if( X的估价值小于CLOSE表的估价值 ) 更新CLOSE表中的估价值; 把X节点放入OPEN //取最小路径的估价值
if(X not in both) 求X的估价值; 并将X插入OPEN表中; //还没有排序 } 将n节点插入CLOSE表中; 按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小,从最小路径的节点向下进行。
}
关于寻路:可以用开源的 RecastNavigation ,里面就有上述算法的实现和demo,支持unity 3d的寻路。
可以用来做地图服务器的案例。 https://github.com/memononen/recastnavigation
unity 3d导航数据的导出要将任意的 Mesh 转换成 rcPolyMes,生成相应的多边形和邻边;这里每个多边形设置为基础的三角形, 然后用内建的函数来优化合并多边形,接着再建立邻边即可,这样就可以得出最优化的 NavMesh 最终数据。
注意:Unity 在导出 NavMesh的数据是包含 NavMesh 中得多边形 Poly信息,可以利用这个直接建立多边形,这样下来数据最接近unity本身的数据。
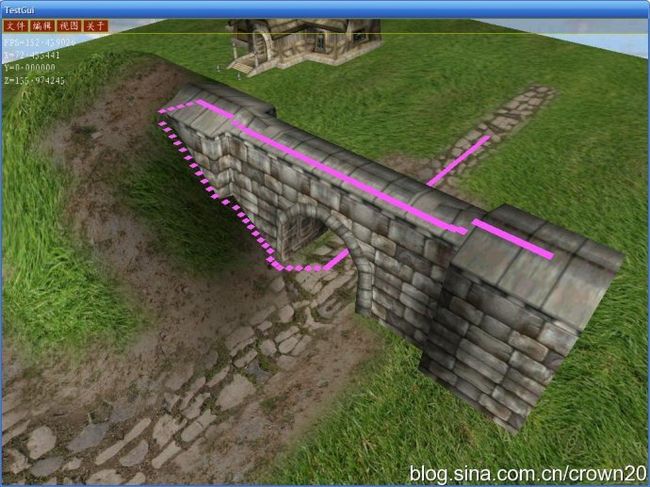
图1旱桥的寻路(粉红色块为路径)
当场景的碰撞使用3D以后相关的寻路也应该具有3D寻路功能,由于引擎中的碰撞格分为多层,所以在开启一个节
点的时候就需要将每一层进行判断,判断条件主要是2个a碰撞格不能为红色b高度差不能超过一定的范围,为了寻路更有效率,增加了一个高度方向的启发值,当两个节点在平面方向与目标距离相等,但高度方向有区别那么与目标高度相差较小的节点优先遍历,其它的过程与2D的a*寻路算法没什么区别。我的寻路算法中使用了二叉堆管理Open表,代码如下,供大家参考,SOpenMask是节点的结构定义,AddOpenMask函数功能是将一个节
点放入Open表中,GetMinOpenMask函数是从Open表中取出具有最小权值的节点,上图是3d a*寻路算法的结果
演示。
struct SOpenMask
{
:
:
SOpenMask *pFather;
SOpenMask *pLeft;
SOpenMask *pRight;
};
int CAStarTrace::AddOpenMask( SOpenMask* pOpenMask, SOpenMask* pHead )
{
if( pHead == NULL )
{
m_pOpenHead = pOpenMask;
return 0;
}
if( pHead->nDistance <= pOpenMask->nDistance )
{
if( pHead->pRight == NULL )
{
pHead->pRight = pOpenMask;
pOpenMask->pFather = pHead;
}
else
AddOpenMask( pOpenMask, pHead->pRight );
}
else
{
if( pHead->pLeft == NULL )
{
pHead->pLeft = pOpenMask;
pOpenMask->pFather = pHead;
}
else
AddOpenMask( pOpenMask, pHead->pLeft );
}
return 0;
}
SOpenMask* CAStarTrace::GetMinOpenMask( SOpenMask* pHead )
{
if( pHead == NULL )
return NULL;
if( pHead->pLeft == NULL )
{
SOpenMask * pMinNode = pHead;
if( pHead->pFather == NULL )
{
m_pOpenHead = pHead->pRight;
if( m_pOpenHead )
m_pOpenHead->pFather = NULL;
}
else
{
pHead->pFather->pLeft = pHead->pRight;
if( pHead->pRight )
pHead->pRight->pFather = pHead->pFather;
}
return pMinNode;
}
else
return GetMinOpenMask( pHead->pLeft );
}