字符串匹配 — BM算法
和Horspool不同的是,算法在失配时不光要看那个不配对的字符,而且还要看已经有多少个字符成功配对,把这两个信息相结合得出模式需要移动的距离。此算法在开始匹配之前需要建立两个表:坏符号移动表和好后缀移动表。坏符号移动表的求法和Horspool的求法一样,但好后缀移动表的计算就有一点复杂了。
运行结果:
关于BM算法,这里有一篇好文章,帮助快速理解:
http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html
代码如下:
#include <iostream>
#include <string>
#include <map>
#include <vector>
#include <algorithm>
using namespace std;
// 计算坏符号移动表
void Get_Bad_Char_Table(const string &text, const string &pattern, map<char, int> &next)
{
int text_len = text.size();
int pattern_len = pattern.size();
for (int i = 0; i < text_len; i++)
next.insert(make_pair(text[i], pattern_len));
for (int i = 0; i < pattern_len - 1; i++)
next[pattern[i]] = pattern_len - 1 - i;
}
// 计算好后缀移动表
void Get_Good_Suffix_Table(const string &pattern, vector<int> &good_suffix)
{
int pattern_len = pattern.size();
const char *p_begin = pattern.c_str();
int save_index, save_len;
bool is_first = true;
for (int i = pattern_len - 1; i > 0; i--)
{
save_index = save_len = -1;
for (int j = i; j < pattern_len; j++)
{
int suffix_len = pattern_len - j;
if (suffix_len == 1)
{
for (int k = 0; k < pattern_len - suffix_len; k++)
{
if (strncmp(p_begin + k, p_begin + j, suffix_len) == 0)
{
save_index = k;
save_len = suffix_len;
if (is_first == false)
break;
}
}
if (is_first == true)
is_first = false;
}
else
{
for (int k = 0; k < pattern_len - suffix_len; k++)
{
if (strncmp(p_begin + k, p_begin + j, suffix_len) == 0)
{
save_index = k;
save_len = suffix_len;
break;
}
}
if (save_index != -1 && save_len != -1)
break;
}
}
if (save_index != -1 && save_len != -1)
good_suffix.push_back(pattern_len - save_index - save_len);
else
good_suffix.push_back(pattern_len);
}
}
void BM(const string &text, const string &pattern, vector<int> &result)
{
int text_len = text.size();
int pattern_len = pattern.size();
map<char, int> bad_char; // 保存坏字符的表
vector<int> good_suffix; // 保存好后缀的表
Get_Bad_Char_Table(text, pattern, bad_char);
Get_Good_Suffix_Table(pattern, good_suffix);
for (int i = pattern_len - 1; i < text_len; /* NULL */)
{
int text_pos = i;
int pattern_pos;
int suffix_len = 0; // 匹配字符数
for (pattern_pos = pattern_len - 1; pattern_pos >= 0; /* NULL */)
{
if (text[text_pos] == pattern[pattern_pos])
{
text_pos--;
pattern_pos--;
suffix_len++;
}
else
{
if (suffix_len == 0) // 和Horspool算法相同
{
i += bad_char[text[i]];
break;
}
else
{
int d1 = bad_char[text[text_pos]] - suffix_len;
int d2 = good_suffix[suffix_len - 1]; // 注意这里的-1
i += max(d1, d2);
break;
}
}
}
if (pattern_pos < 0)
{
result.push_back(i - pattern_len + 1); // 完全匹配时的起始位置
i++;
}
}
}
int main()
{
string text = "hello world good google Nestle people google hello this is a test google";
string pattern = "google";
vector<int> result;
BM(text, pattern, result);
int cnt = 1;
for (vector<int>::iterator iter = result.begin(); iter != result.end(); ++iter)
cout << "match " << cnt++ << " = " << *iter << endl;
system("pause");
return 0;
}
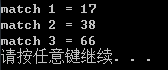
运行结果:
效率分析:
BM算法的最差效率是线性的,当字母表规模很大时,速度非常快。
参考:
《算法设计与分析基础》 P197-P201.