求对称字符串的最大长度算法
程序员面试100题之一:对称字符串的最大长度
分析:可能很多人都写过判断一个字符串是不是对称的函数,这个题目可以看成是该函数的加强版。
要判断一个字符串是不是对称的,不是一件很难的事情。我们可以先得到字符串首尾两个字符,判断是不是相等。如果不相等,那该字符串肯定不是对称的。否则我们接着判断里面的两个字符是不是相等,以此类推。基于这个思路,我们不难写出如下代码:
- /*
- 判断起始指针为pBegin,结束指针为pEnd的字符串是否对称
- */
- bool IsSymmetrical(char* pBegin, char* pEnd)
- {
- if(pBegin == NULL || pEnd == NULL || pBegin > pEnd)
- return false;
- while(pBegin < pEnd)
- {
- if(*pBegin != *pEnd)
- return false;
- pBegin++;
- pEnd --;
- }
- return true;
- }
要判断一个字符串pString是不是对称的,我们只需要调用IsSymmetrical(pString, &pString[strlen(pString) – 1])就可以了。
现在我们试着来得到对称子字符串的最大长度。最直观的做法就是得到输入字符串的所有子字符串,并逐个判断是不是对称的。如果一个子字符串是对称的,我们就得到它的长度。这样经过比较,就能得到最长的对称子字符串的长度了。于是,我们可以写出如下代码:
- /*
- 取得所有对称子串的最大长度
- 时间复杂度: O(n^3)
- */
- int GetLongestSymmetricalLength_1(char* pString)
- {
- if(pString == NULL)
- return 0;
- int symmeticalLength = 1;
- char* pFirst = pString;
- int length = strlen(pString);
- while(pFirst < &pString[length - 1])
- {
- char* pLast = pFirst + 1;
- while(pLast <= &pString[length - 1])
- {
- if(IsSymmetrical(pFirst, pLast))
- {
- int newLength = pLast - pFirst + 1;
- if(newLength > symmeticalLength)
- symmeticalLength = newLength;
- }
- pLast++;
- }
- pFirst++;
- }
- return symmeticalLength;
- }
我们来分析一下上述方法的时间效率。由于我们需要两重while循环,每重循环需要O(n)的时间。另外,我们在循环中调用了IsSymmetrical,每次调用也需要O(n)的时间。因此整个函数的时间效率是O(n^3)。
通常O(n^3)不会是一个高效的算法。如果我们仔细分析上述方法的比较过程,我们就能发现其中有很多重复的比较。假设我们需要判断一个子字符串具有aAa的形式(A是aAa的子字符串,可能含有多个字符)。我们先把pFirst指向最前面的字符a,把pLast指向最后面的字符a,由于两个字符相同,我们在IsSymtical函数内部向后移动pFirst,向前移动pLast,以判断A是不是对称的。接下来若干步骤之后,由于A也是输入字符串的一个子字符串,我们需要再一次判断它是不是对称的。也就是说,我们重复多次地在判断A是不是对称的。
造成上述重复比较的根源在于IsSymmetrical的比较是从外向里进行的。在判断aAa是不是对称的时候,我们不知道A是不是对称的,因此需要花费O(n)的时间来判断。下次我们判断A是不是对称的时候,我们仍然需要O(n)的时间。
如果我们换一种思路,我们从里向外来判断。也就是我们先判断子字符串A是不是对称的。如果A不是对称的,那么向该子字符串两端各延长一个字符得到的字符串肯定不是对称的。如果A对称,那么我们只需要判断A两端延长的一个字符是不是相等的,如果相等,则延长后的字符串是对称的。因此在知道A是否对称之后,只需要O(1)的时间就能知道aAa是不是对称的。
我们可以根据从里向外比较的思路写出如下代码:
- /*
- 取得所有对称子串的最大长度
- 时间复杂度: O(n^2)
- */
- int GetLongestSymmetricalLength(char* pString)
- {
- if(pString == NULL)
- return 0;
- int symmeticalLength = 1;
- char* pChar = pString;
- while(*pChar != '\0')
- {
- // Substrings with odd length
- char* left = pChar - 1;
- char* right = pChar + 1;
- while(left >= pString && *right != '\0' && *left == *right)
- {
- left--;
- right++;
- }
- int newLength = right - left - 1; //退出while循环时,*left != *right
- if(newLength > symmeticalLength)
- symmeticalLength = newLength;
- // Substrings with even length
- left = pChar;
- right = pChar + 1;
- while(left >= pString && *right != '\0' && *left == *right)
- {
- left--;
- right++;
- }
- newLength = right - left - 1; //退出while循环时,*left != *right
- if(newLength > symmeticalLength)
- symmeticalLength = newLength;
- pChar++;
- }
- return symmeticalLength;
- }
由于子字符串的长度可能是奇数也可能是偶数。长度是奇数的字符串是从只有一个字符的中心向两端延长出来,而长度为偶数的字符串是从一个有两个字符的中心向两端延长出来。因此我们的代码要把这种情况都考虑进去。
在上述代码中,我们从字符串的每个字符串两端开始延长,如果当前的子字符串是对称的,再判断延长之后的字符串是不是对称的。由于总共有O(n)个字符,每个字符可能延长O(n)次,每次延长时只需要O(1)就能判断出是不是对称的,因此整个函数的时间效率是O(n^2)。
回文串定义:“回文串”是一个正读和反读都一样的字符串,比如“level”或者“noon”等等就是回文串。
回文子串,顾名思义,即字符串中满足回文性质的子串。
经常有一些题目围绕回文子串进行讨论,比如 HDOJ_3068_最长回文,求最长回文子串的长度。朴素算法是依次以每一个字符为中心向两侧进行扩展,显然这个复杂度是O(N^2)的,关于字符串的题目常用的算法有KMP、后缀数组、AC自动机,这道题目利用扩展KMP可以解答,其时间复杂度也很快O(N*logN)。但是,今天笔者介绍一个专门针对回文子串的算法,其时间复杂度为O(n),这就是manacher算法。
大家都知道,求回文串时需要判断其奇偶性,也就是求aba和abba的算法略有差距。然而,这个算法做了一个简单的处理,很巧妙地把奇数长度回文串与偶数长度回文串统一考虑,也就是在每个相邻的字符之间插入一个分隔符,串的首尾也要加,当然这个分隔符不能再原串中出现,一般可以用‘#’或者‘$’等字符。例如:
原串:abaab
新串:#a#b#a#a#b#
这样一来,原来的奇数长度回文串还是奇数长度,偶数长度的也变成以‘#’为中心的奇数回文串了。
接下来就是算法的中心思想,用一个辅助数组P记录以每个字符为中心的最长回文半径,也就是P[i]记录以Str[i]字符为中心的最长回文串半径。P[i]最小为1,此时回文串为Str[i]本身。
我们可以对上述例子写出其P数组,如下
新串: # a # b # a # a # b #
P[] : 1 2 1 4 1 2 5 2 1 2 1
我们可以证明P[i]-1就是以Str[i]为中心的回文串在原串当中的长度。
证明:
1、显然L=2*P[i]-1即为新串中以Str[i]为中心最长回文串长度。
2、以Str[i]为中心的回文串一定是以#开头和结尾的,例如“#b#b#”或“#b#a#b#”所以L减去最前或者最后的‘#’字符就是原串中长度的二倍,即原串长度为(L-1)/2,化简的P[i]-1。得证。
依次从前往后求得P数组就可以了,这里用到了DP(动态规划)的思想,也就是求P[i]的时候,前面的P[]值已经得到了,我们利用回文串的特殊性质可以进行一个大大的优化。我先把核心代码贴上:
- for(i=1;i<n;i++)
- {
- if(MaxId>i)
- {
- p[i]=Min(p[2*id-i],MaxId-i);
- }
- else
- {
- p[i]=1;
- }
- while(Str[i+p[i]]==Str[i-p[i]])
- {
- p[i]++;
- }
- if(p[i]+i>MaxId)
- {
- MaxId=p[i]+i;
- id=i;
- }
- }
- if(MaxId>i)
- {
- p[i]=Min(p[2*id-i],MaxId-i);
- }

j=2*id-1即为i关于id的对称点,根据对称性,P[j]的回文串也是可以对称到i这边的,但是如果P[j]的回文串对称过来以后超过MaxId的话,超出部分就不能对称过来了,如下图,所以这里P[i]为的下限为两者中的较小者,p[i]=Min(p[2*id-i],MaxId-i)。
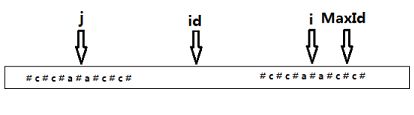
算法的有效比较次数为MaxId次,所以说这个算法的时间复杂度为O(n)。
附HDOJ_3068_最长回文代码:
- #include <stdio.h>
- #define M 110010
- char b[M],a[M<<1];
- int p[M<<1];
- int Min(int a,int b)
- {
- return a<b?a:b;
- }
- int main(void)
- {
- int i,n,id,MaxL,MaxId;
- while(scanf("%s",&b[1])!=EOF)
- {
- MaxL=MaxId=0;
- for(i=1;b[i]!='\0';i++)
- {
- a[(i<<1)]=b[i];
- a[(i<<1)+1]='#';
- }
- a[0]='?';a[1]='#';
- n=(i<<1)+2;a[n]=0;
- MaxId=MaxL=0;
- for(i=1;i<n;i++)
- {
- if(MaxId>i)
- {
- p[i]=Min(p[2*id-i],MaxId-i);
- }
- else
- {
- p[i]=1;
- }
- while(a[i+p[i]]==a[i-p[i]])
- {
- p[i]++;
- }
- if(p[i]+i>MaxId)
- {
- MaxId=p[i]+i;
- id=i;
- }
- if(p[i]>MaxL)
- {
- MaxL=p[i];
- }
- }
- printf("%d\n",MaxL-1);
- }
- return 0;
- }