PAT1034 有理数四则运算(20)

本题要求编写程序，计算2个有理数的和、差、积、商。

输入格式：

输入在一行中按照“a1/b1 a2/b2”的格式给出两个分数形式的有理数，其中分子和分母全是整型范围内的整数，负号只可能出现在分子前，分母不为0。

输出格式：

分别在4行中按照“有理数1 运算符 有理数2 = 结果”的格式顺序输出2个有理数的和、差、积、商。注意输出的每个有理数必须是该有理数的最简形式“k a/b”，其中k是整数部分，a/b是最简分数部分；若为负数，则须加括号；若除法分母为0，则输出“Inf”。题目保证正确的输出中没有超过整型范围的整数。

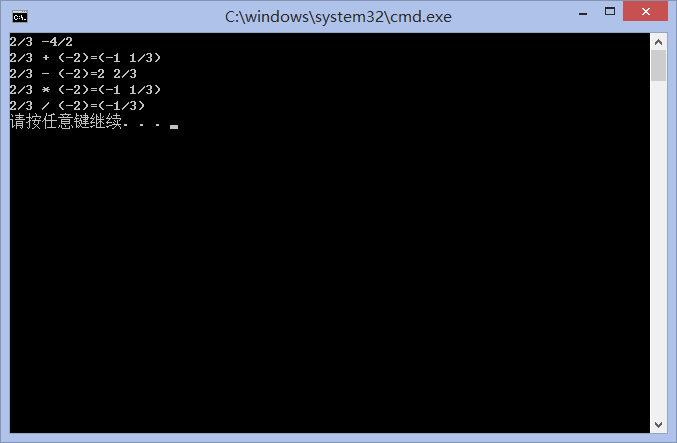
输入样例1：
2/3 -4/2
输出样例1：
2/3 + (-2) = (-1 1/3)
2/3 - (-2) = 2 2/3
2/3 * (-2) = (-1 1/3)
2/3 / (-2) = (-1/3)
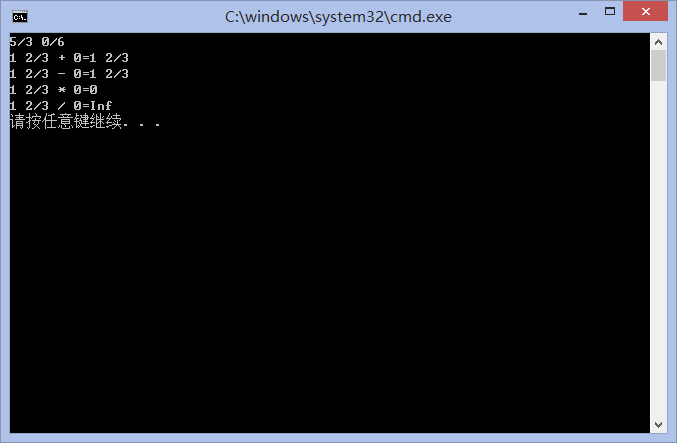
输入样例2：
5/3 0/6
输出样例2：
1 2/3 + 0 = 1 2/3
1 2/3 - 0 = 1 2/3
1 2/3 * 0 = 0
1 2/3 / 0 = Inf

解题思路：此题比较繁琐，分模块编写代码
模块一，声明含分子与分母组成的结构体

struct Numbers{
    int FenMu;
    int FenZi;
};

模块二，找出最大公约数

int CommonDivisor(int a, int b){
    int temp = 0;
    while (b != 0)
    {
        temp = a%b;//取余
        a = b;//交换
        b = temp;
    }
    return a;//返回目标值
}

模块三，将输入的String字符串转化为整型的分子与分母的形式

Numbers Transform(string str){
    Numbers num;
    int len = str.length();
    int i = len - 1;
    int tmp = 0, k = 0;
    while (str[i] != '/'){
        tmp += (str[i] - '0')*pow(10, k);
        ++k;
        --i;
    }
    num.FenMu = tmp;
    --i;
    k = 0;
    tmp = 0;
    if (str[0] != '-'){
        while (i >= 0){
            tmp += (str[i] - '0')*pow(10, k);
            --i;
            ++k;
        }
    }
    if (str[0] == '-'){
        while (i > 0){
            tmp += (str[i] - '0')*pow(10, k);
            --i;
            ++k;
        }
        tmp = -1 * tmp;
    }
    num.FenZi = tmp;
    return num;
}

模块四，化简输出

void Simplification(Numbers num){
    int a = num.FenZi;
    int b = num.FenMu;
    int cd = CommonDivisor(a, b);
    cd=abs(cd);
    a = a / cd;
    b = b / cd;
    if (a > 0&&b>0){
        if (a%b == 0){
            cout << a / b;
        }
        else if (abs(a) > b){
             cout << a / b << " " << a%b << '/' << b;
        }
        else{
            cout << a << '/' << abs(b);
        }
    }
    else if (a < 0||b<0){
        a = abs(a);
        b = abs(b);
        if (a%b == 0){
             cout << "(-" << a / b << ")";
        }
        else if (a >b){
        cout << "(-" << a / b << " " << a % b << '/' << b << ")";
        }
        else{
         cout << "(-" << a << '/' << b << ")";
        }
    }
    else cout << '0';

}

分别再以四个模块实现加减乘除

void ADDf(string a, string b){
    Numbers numa, numb,numResult;
    numa = Transform(a);
    numb = Transform(b);
    numResult.FenZi = (numa.FenZi*numb.FenMu) + (numa.FenMu*numb.FenZi);
    numResult.FenMu = (numa.FenMu*numb.FenMu);
    Simplification(numa);
    cout << " + ";
    Simplification(numb);
    cout << "=";
    Simplification(numResult);
    cout << endl;
}
void SUBf(string a, string b){
    Numbers numa, numb, numResult;
    numa = Transform(a);
    numb = Transform(b);
    numResult.FenZi = (numa.FenZi*numb.FenMu) - (numa.FenMu*numb.FenZi);
    numResult.FenMu = (numa.FenMu*numb.FenMu);
    Simplification(numa);
    cout << " - ";
    Simplification(numb);
    cout << "=";
    Simplification(numResult);
    cout << endl;
}
void MULf(string a, string b){
    Numbers numa, numb, numResult;
    numa = Transform(a);
    numb = Transform(b);
    numResult.FenZi = numa.FenZi*numb.FenZi;
    numResult.FenMu = (numa.FenMu*numb.FenMu);
    Simplification(numa);
    cout << " * ";
    Simplification(numb);
    cout << "=";
    Simplification(numResult);
    cout << endl;
}
void DIVf(string a, string b){
    Numbers numa, numb, numResult;
    numa = Transform(a);
    numb = Transform(b);
    numResult.FenZi = numa.FenZi*numb.FenMu;
    numResult.FenMu = numa.FenMu*numb.FenZi;
    Simplification(numa);
    cout << " / ";
    Simplification(numb);
    cout << "=";
    if (numResult.FenMu == 0)cout << "Inf";
    else Simplification(numResult);
    cout << endl;
}

主函数

int main(){
    string a = "",b="";
    cin >> a >> b;
    ADDf(a, b);
    SUBf(a, b);
    MULf(a, b);
    DIVf(a, b);
    return 0;
}

输出结果—1

输出结果—2