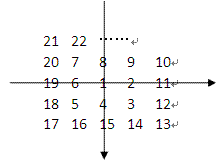程序员面试宝典——螺旋队列解法解析2
续写《程序员面试宝典——螺旋队列解法解析》
先附上c++代码,看懂的人可以不必看代码下面的举例说明了。
#include <iostream> using namespace std; #define max(a,b) ((a)>(b)?(a):(b)) #define abs(a) ((a)>0?(a):-(a)) //螺旋队列解法 int foo(int x, int y){ int t = max(abs(x), abs(y)); //int u = 2*t; //int v = (2*t-1)*(2*t-1); int u = t + t; int v = u - 1; v = v * v + t; if(y == t){ v += u - x; } else if(x == -t){ v += 2*u - y; } else if(y == -t){ v += 3*u + x; } else{ // x==t的情况必须放在y==-t的后面 v += y; } return v; } int main() { int x, y; for (y=-4 ; y<=4 ; y++){ for (x=-4 ; x<=4 ; x++){ printf("%5d", foo(x,y)); } cout<<endl; } printf("请输入数字的坐标,以空格键分离,以回车键结束/n"); while(scanf("%d%d", &x, &y) == 2) printf("%d/n", foo(x,y)); return 0; }
举例说明:
假定要求坐标为(1,-1)的数字的值。
结论:从图上大家可以看到,坐标为(1,-1)的数字是9,它在圈1上。
下面我就按照上一篇文章《程序员面试宝典——螺旋队列解法解析》中的步骤走一遍。
1.确定圈号t。
t = max(|x|, |y|);
这里|x| = 1, |y| = 1,所以t = max(1, 1) = 1。
2.确定圈t-1的最大值。
max(t-1) = (2t - 1)2 。
这里max(t - 1) = max(0) = 1。
3.确定数字v的值
数字v的值 = 前一圈的最大值 + 顺时针步长。
前一圈的最大值在第2步中已经求了,为1。
下面按照分类标准,求顺时针步长。
边长u = 2t = 2。符合上图2~9围成的是一个边长为2 的正方形。
坐标(1, -1),首先按照4个分类的顺序,不满足前两个分类的条件(y = t = 1,x = -t = -1),但它同时满足后两个条件(y = -t = -1, x = t = 1)。由于坐标先满足条件3,所以按照条件3的公式来计算:
顺时针步长 = 3u + u/2 + x = 3 * 2 + 2/2 + 1 = 8
v = 前一圈的最大值+顺时针步长 = 1 + 8 = 9。
解毕。
这里对顺时针步长公式,做一下解释,为什么是这样的呢?
所谓顺时针步长,就是从前一圈的最大值位置数起,按照顺时针方向沿着当前圈行走,需要走多少步能到达所求坐标。
本例中,从1这个位置数起,沿着顺时针方向依次走过2,3,4,5,……,9,每经过1个数字即走过1个步长,走到9走过了8个步长。
到达 边y = -t上的数字,需要依次走过 边x = t, y = t,x = -t 3边,故顺时针步长中有3u这一项。
u/2使得步长 到达 y = -t 与y轴的交点上,此时顺时针步长就只与x坐标相关了,x为1,则步长加1,x为-1,则步长-1.
其它3个顺时针步长公式类推。