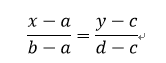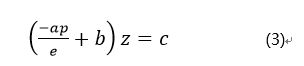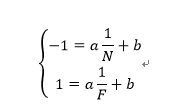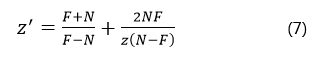OpenGL中的深度值winz与相机空间z值的关系推导
待渲染的照相机空间中的深度经常定义为近距 near 到远距 far 之间的 z 值,在透视变换之后,得到新的 z' 值,下面将对z'与z值之间的关系进行推导:
在此之前,先介绍两个必要的基础知识:
1、简单的线性插值
这是在图形学中普遍使用的基本技巧,我们在很多地方都会用到,比如2D位图的放大、缩小,Tweening变换,以及我们即将看到的透视投影变换等等。基本思想是:给一个x属于[a, b],找到y属于[c, d],使得x与a的距离比上ab长度所得到的比例,等于y与c的距离比上cd长度所得到的比例,用数学表达式描述很容易理解:
这样,从a到b的每一个点都与c到d上的唯一一个点对应。有一个x,就可以求得一个y。
此外,如果x不在[a,b]内,比如x < a或者x > b,则得到的y也是符合y < c或者y> d,比例仍然不变,插值同样适用。
2、深度插值
当3D图形处理器将一个三角形渲染到屏幕的时候,需要在屏幕上对三角形以逐行扫描的方式进行光栅化。三角形的顶点除了携带在摄像机空间中的位置信息外,还携带有其他信息,比如深度、颜色、亮度等等,在光栅化的过程中必须在三角形的表面上对这些信息进行插值。当画出三角形的一条扫描线时,扫描线上的每个像素的信息,是对扫描线的左右端点处已知信息值进行插值运算而得到的。
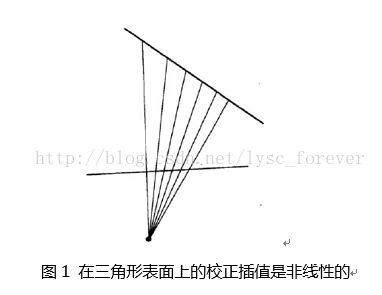
如图1所示,对三角形表面的校正插值是非线性的,这是因为对于投影面上相等的空间步长,它们在三角形面上对应的步长会随着离摄像机的距离的增加而变长。
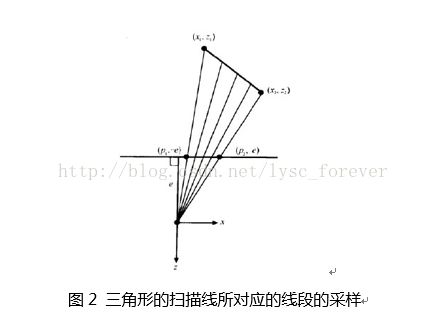
下面讨论深度插值,在图2给出了位于xz平面上的一条线段,它对应于三角形的一条扫描线。在光栅化的过程中要对该线段上的点进行采样,采样时先在投影平面上取空间等距点(这里的空间等距点对应于屏幕上的像素点),然后求通过这些等距点的光线与线段的交点,得到的所有交点就是采样点。如果线段所在的直线不通过原点(否则三角形是边界可见的,三角形本身不可见),则可以用下面的方程来描述这条直线
对于直线上的一点(x,z),可以引一条从原点(摄像机位置)指向点(x,z)的射线,并求得射线与投影平面的交点。在投影平面上的z坐标恒为-e。可以从图2给出的相似三角形关系中导出下面的关系式,从而求得点(x,z)在投影平面上所对应x的坐标p
解关于x的方程,并将x带回等式(1),可以将直线的方程重写为如下形式:
将上式改写为只有一边出现1/z的形式,可以得到便于以后使用的方程:
设线段的两个端点为(x1,z1)和(x2,z2),它们在投影平面上的投影分别为(p1,-e)和(p2,-e),同时设p3=(1-t)p1+tp2( t大于0小于1)是投影平面上插值点的x坐标,这里需求出射线穿过点(p3,-e)与三角形面的交点(x3,z3)的z坐标。将p3=(1-t)p1+tp2和z3代到式(4),可以得到
这个结果表明,在整个三角面上,z坐标的倒数恰好是按线性的方式进行插值的。
3、z'与z值之间的关系的推导
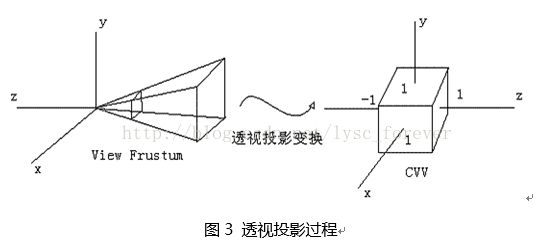
有了上面两个理论知识,我们开始推导z'与z值之间的关系。首先我们先介绍一下透视投影,透视投影的目的就是将上面的视锥体(图3)转换为一个立方体,转换后,视锥体的前剪裁平面的右上角点变为立方体的前平面的中心。由图可知,这个变换的过程是将视锥体较小的部分放大,较大的部分缩小,以形成最终的立方体。这就是投影变换会产生近大远小的效果的原因。变换后的x坐标范围是[-1, 1],y坐标范围是[-1, 1],z坐标范围是[-1,1]。
我们一步一步来,我们先从一个方向考察投影关系。上图是右手坐标系中顶点在相机空间中的情形。设P(x,z)是经过相机变换之后的点,视锥体由eye——摄像机位置,np——近裁剪平面,fp——远裁剪平面组成。N是眼睛到近裁剪平面的距离,F是眼睛到远裁剪平面的距离。投影面可以选择任何平行于近裁剪平面的平面,这里我们选择近裁剪平面作为投影平面。设P’(x’,z’)是投影之后的点,则有z’ = N。通过相似三角形性质,我们有关系:
同理,有
这样,我们便得到了P投影后的点P’
最后看z',当视锥体内的点投影到近剪裁平面的时候,实际上这个z'值已经意义不大了,因为所有位于近剪裁平面上的点,其z'值都是N,但是我们不可以抛弃这个z'值,因为对于3D图形管理来说,为了便于进行后面的片元操作,例如z缓冲区消隐算法,有必要把投影之前的z保存下来,方便后面使用。所以z'坐标可以直接保存p点的z值。在光栅化之前,由前面关于深度插值的知识可知,我们需要对z坐标的倒数进行插值,所以可以将z'写成z的一次表达式形式,如下:
在映射前,z的范围是[N,F],这里N和F分别是近远两个剪裁平面到原点的距离,在映射后,z'的范围是[-1,1],将数据代入上面的一次式,可得下面的方程组:
解这个方程组得到:
将求得的a、b代入式(6),可得:
其中 z 是照相机空间的坐标z值,结果 z' 是在 -1 到 1 之间归一化之后的值,其中近裁剪平面位于 -1 处,远裁剪平面位于 1 处。在这个范围之外的相应点在视锥体之外,不需要进行渲染。
至此,z'与z值之间的关系推导完成。
之后,在视口变换期间进行深度坐标的变换,以后便将其存储在深度缓冲区中。在OpenGL中,可以使用glDepthRange()函数,对z值进行缩放,使它位于我们所需要的范围之内,在默认情况下,z坐标总被认为位于0.0~1.0的范围之间。