算法-深度优先搜索

在图上寻找路径

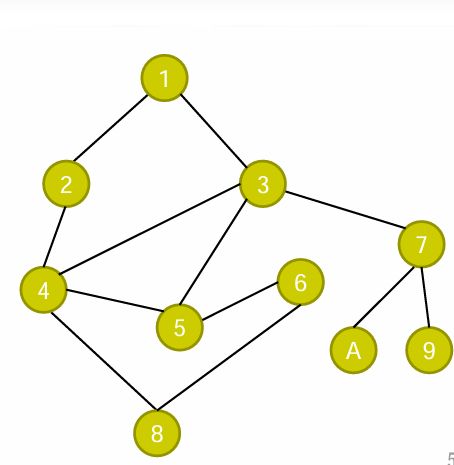
在图上如何寻找从1到8的路径? 一种策略：只要能发现没走过的点， 就走到它。有多个点可走就随便挑一 个，如果无路可走就回退，再看有没有没走过的点可走。

运气最好：1->2->4->8 2

运气稍差：1->2->4->5->6->8

运气坏： 1->3->7->9=>7->A=>7=>3->5->6->8 （双线箭头表示回退）

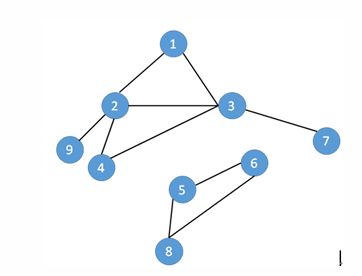
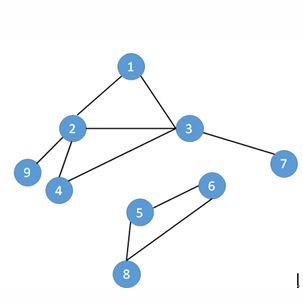
不连通的图，无法从节点1走到节点8。完整的尝试过程可能如下： 1->2->4->3->7=>3=>4=>2 >9=>2=>1。

深度优先搜索(Depth-First-Search)

从起点出发，走过的点要做标记，发现有没走过的点，就随意挑一个往前走，走不 了就回退，此种路径搜索策略就称为“深度优先搜索”，简称“深搜”。 其实称为“远度优先搜索”更容易理解些。因为这种策略能往前走一步就往前走一 步，总是试图走得更远。所谓远近(或深度），就是以距离起点的步数来衡量的。

城堡问题

计算城堡一共有多少房间， 最大的房间有多大。城堡 被分割成m×n(m≤50， n≤50)个方块，每个方块可 以有0~4面墙。

输入

•  程序从标准输入设备读入数据。
•  第一行是两个整数，分别是南北向、东西向的方块数。
•  在接下来的输入行里，每个方块用一个数字(0≤p≤50)描述。用一个数 字表示方块周围的墙，1表示西墙，2表示北墙，4表示东墙，8表示南 墙。每个方块用代表其周围墙的数字之和表示。城堡的内墙被计算两 次，方块(1,1)的南墙同时也是方块(2,1)的北墙。
•  输入的数据保证城堡至少有两个房间。

 输出

•  城堡的房间数、城堡中最大房间所包括的方块数。
•  结果显示在标准输出设备上。

解题

• 把方块看作是节点，相邻两个方块之间如果没 有墙，则在方块之间连一条边，这样城堡就能 转换成一个图。
•  求房间个数，实际上就是在求图中有多少个极 大连通子图。
•  一个连通子图，往里头加任何一个图里的其他 点，就会变得不连通，那么这个连通子图就是 极大连通子图。（如：(8,5,6))

对每一个房间，深度优先搜索，从而给这个房间能够到达的所有位置染色。最后统计一共用 了几种颜色，以及每种颜色的数量。

1 1 2 2 3 3 3

1 1 1 2 3 4 3

1 1 1 5 3 5 3

1 5 5 5 5 5 3

从而一共有5个房间，最大的房间（1）占据9 个格子

#include 
#include 
#include 
#include 
using namespace std;
int R,C;
int rooms[60][60];
int color[60][60];
int maxRoomArea=0;
int roomNum = 0;
int roomArea;
//深度优先搜索函数
void Dfs(int i,int k) {
    //如果该房间已经访问过，则返回
    if (color[i][k])
        return;
    //房间面积加1
    ++roomArea;
    //将该房间标记为已访问
    color[i][k]=1;
    //如果该房间与西边的房间连通，则继续搜索
    if( (rooms[i][k] & 1) == 0 ) Dfs(i,k-1);   //向西走
    //如果该房间与北边的房间连通，则继续搜索
    if( (rooms[i][k] & 2) == 0 ) Dfs(i-1,k);   //向北
    //如果该房间与东边的房间连通，则继续搜索
    if( (rooms[i][k] & 4) == 0 ) Dfs(i,k+1);  //向东
    //如果该房间与南边的房间连通，则继续搜索
    if( (rooms[i][k] & 8) == 0 ) Dfs(i+1,k);  //向南
}
int main() {
    //输入行数和列数
    cin>>R>>C;
    //输入每个房间的连通情况
    for (int i = 1; i <=R; ++i)
        for (int j = 1; j <=C; ++j)
            cin>>rooms[i][j];
    //遍历每个房间
    for (int i = 1; i <=R; ++i) {
        for (int k = 1; k <=C; ++k)
            //如果该房间未被访问过，则进行深度优先搜索
            if (!color[i][k]){
                //房间数量加1
                ++roomNum; roomArea=0;
                //进行深度优先搜索
                Dfs(i,k);
                //更新最大房间面积
                maxRoomArea=max(maxRoomArea,roomArea);
            }
        }
    //输出房间数量和最大房间面积
    cout<

输入

4
7 

输出
11 6 11 6 3 10 6 
7 9 6 13 5 15 5 
1 10 12 7 13 7 5 
13 11 10 8 10 12 13
5
9

踩方格

有一个方格矩阵，矩阵边界在无穷远处。我们做如下假设：

a.每走一步时，只能从当前方格移动一格，走到某个相邻的方格上；

b. 走过的格子立即塌陷无法再走第二次；

c. 只能向北、东、西三个方向走；

请问：如果允许在方格矩阵上走n步(n<=20)，共有多少种不同的方案。 2种走法只要有一步不一样，即被认为是不同的方案。

递归 从(i,j) 出发，走n步的方案数，等于以下三项之和：

从(i+1,j)出发，走n-1步的方案数。前提：(i+1,j)还没走过 从(i,j+1)出发

走n-1步的方案数。前提：(i,j+1)还没走过 从(i,j-1)出发

走n-1步的方案数。前提：(i,j-1)还没走过

#include 
#include 
#include 
#include 
using namespace std;
#include 
#include 
using namespace std;
// 定义一个二维数组，用于记录每个位置是否被访问过
int visited[30][50];
// 定义一个函数，用于计算从(i,j)位置出发，走n步的方案数
int ways ( int i,int j,int n)
{
    // 如果n为0，说明已经走完了n步，返回1
    if( n == 0)
        return 1;
    // 标记当前位置为已访问
    visited[i][j] = 1;
    int num = 0;
    // 如果当前位置的左边没有被访问过，则递归调用ways函数，计算从左边出发的方案数
    if( ! visited[i][j-1] )
        num+= ways(i,j-1,n-1);
    // 如果当前位置的右边没有被访问过，则递归调用ways函数，计算从右边出发的方案数
    if( ! visited[i][j+1] )
        num+= ways(i,j+1,n-1);
    // 如果当前位置的下边没有被访问过，则递归调用ways函数，计算从下边出发的方案数
    if( ! visited[i+1][j] )
        num+= ways(i+1,j,n-1);
    // 将当前位置标记为未访问
    visited[i][j] = 0;
    // 返回方案数
    return num;
}int main()
{
    int n;
    // 从标准输入读取n的值
    cin >> n;
    // 将visited数组初始化为0
    memset(visited,0,sizeof(visited));
    // 调用ways函数，计算从(0,25)位置出发，走n步的方案数，并输出结果
    cout << ways(0,25,n) << endl;
    return 0;
}

输入5
输出99