Description
Alice owns a construction company in the town of Norainia, famous for its unusually dry weather. In fact, it only rains a few days per year there. Because of this phenomenon, many residents of Norainia neglect to do roof repairs until leaks occur and ruin their floors. Every year, Alice receives a deluge of calls from residents who need the leaks fixed and floor tiles replaced. While exquisite in appearance, Norainia floor tiles are not very water resistant; once a tile becomes wet, it is ruined and must be replaced. This year, Alice plans to handle the rainy days more efficiently than in past years. She will hire extra contractors to dispatch as soon as the calls come in, so hopefully all leaks can be repaired as soon as possible. For each house call, Alice needs a program to help her determine how many replacement tiles a contractor team will need to bring to complete the job.
For a given house, square floor tiles are arranged in a rectangular grid. Leaks originate from one or more known source locations above specific floor tiles. After the first minute, the tiles immediately below the leaks are ruined. After the second minute, water will have spread to any tile that shares an edge with a previously wet tile. This pattern of spreading water continues for each additional minute. However, the walls of a house restrict the water; if a damaged area hits a wall, the water does not penetrate the wall. We assume there are always four outer walls surrounding the entire house. A house may also have a number of additional "inner" walls; each inner wall is comprised of a connected linear sequence of locations (which may or may not be connected to the outer walls or to each other).
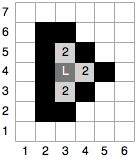
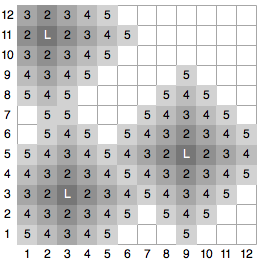
As an example, Figure 1 shows water damage (in gray) that would result from three initial leaks (each marked with a white letter 'L') after each of the first five minutes of time. Tiles labeled '2' become wet during the second minute, tiles labeled '3' become wet during the third minute, and so forth. The black areas designate inner walls that restrict the flow of water. Note that after 5 minutes, a total of 75 tiles have been damaged and will need to be replaced. Figures 2 through 4 show other houses that correspond to the example inputs for this problem.
75 wet tiles

17 wet tiles

4 wet tiles
94 wet tiles
Input
Each house is described beginning with a line having five integral parameters: X Y T L W. Parameters X and Y designate the dimensions of the rectangular grid, with 1 ≤ X ≤ 1000 and 1 ≤ Y ≤ 1000. The coordinate system is one-indexed, as shown in the earlier figures. Parameter T designates the number of minutes that pass before a team of contractors arrives at a house and stops the leaks, with 1 ≤ T ≤ 200000. The parameter L designates the number of leaks, with 1 ≤ L ≤ 100. Parameter W designates the number of inner walls in the house, 0 ≤ W ≤ 100.
The following 2L integers in the data set, on one or more lines, are distinct (x y) pairs that designate the locations of the L distinct leaks, such that 1 ≤ x ≤ X and 1 ≤ y ≤ Y.
If W > 0, there will be 4W additional integers, on one or more lines, that describe the locations of the walls. For each such wall the four parameters (x1,y1), (x2,y2) describe the locations of two ends of the wall. Each wall replaces a linear sequence of adjoining tiles and is either axis-aligned or intersects both axes at a 45 degree angle. Diagonal walls are modeled as a sequence of cells that would just be touching corner to corner. If the two endpoints of a wall are the same, the wall just occupies the single cell at that location. Walls may intersect with each other, but no leak is over a wall.
There will be one or more houses in the data file and a line with a single integer -1 designates the end of the data set.
Output
For each house, display the total number of tiles that are wet after T minutes.
Sample Input
12 12 5 3 5
2 11 3 3 9 5
1 9 6 9 1 7 4 4 7 1 7 4
10 9 10 12 11 4 12 4
9 7 8 1 3
4 3
2 2 6 6 6 2 2 6 8 2 8 2
6 7 50 1 3
3 4
2 2 2 6 3 6 5 4 5 4 3 2
12 12 5 3 0
2 11 3 3 9 5
-1
Sample Output
75
17
4
94
这是一道搜索题,刚开始不知道有时间限制的宽搜怎么弄,后来看了别人的代码知道可以直接在走过的点上记录时间,比如一开始的源点map[i][j]=1,然后每扩展出一个点,该点的map[xx][yy]=map[x][y]+1,当队列最开始的点的时间超过总限制时间的时候就退出,输出t.这里还有一点要注意,当两个源点扩展的点重复时,只要算一次就行了,可以画图。
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int map[1005][1005];
int dir[10][2]={{0,0},{1,0},{0,1},{-1,0},{0,-1}};
struct node{
int x,y;
}q[1111111];
int main()
{
int n,m,tt,l,w,i,j,t,a,b,x2,y2,x3,y3,x,y,xx,yy,h;
while(scanf("%d",&n)!=EOF && n!=-1)
{
scanf("%d%d%d%d",&m,&tt,&l,&w);
memset(map,0,sizeof(map));
for(i=1;i<=l;i++){
scanf("%d%d",&a,&b);
q[i].x=a;
q[i].y=b;
map[a][b]=1;
}
for(i=1;i<=w;i++){
scanf("%d%d%d%d",&x2,&y2,&x3,&y3);{
if(x2>x3){
swap(x2,x3);
swap(y2,y3);
}
if(x2==x3){
if(y2>y3){
swap(y2,y3);
}
for(j=y2;j<=y3;j++){
map[x2][j]=-1;
}
}
else if(y2==y3){
for(j=x2;j<=x3;j++){
map[j][y2]=-1;
}
}
else{
if(y2>y3){
for(j=y2;j>=y3;j--){
map[x2][j]=-1;
x2++;
}
}
else {
for(j=y2;j<=y3;j++){
map[x2][j]=-1;
x2++;
}
}
}
}
}
h=1;t=l;
while(h<=t)
{
x=q[h].x;
y=q[h].y;
h++;
if(map[x][y]>=tt)break;
for(i=1;i<=4;i++){
xx=x+dir[i][0];
yy=y+dir[i][1];
if(xx>=1 && xx<=n && yy>=1 && yy<=m && map[xx][yy]==0){
map[xx][yy]=map[x][y]+1;
t++;
q[t].x=xx;
q[t].y=yy;
}
}
}
printf("%d\n",t);
}
return 0;
}



