学习UKK后缀树构造算法

学习了UKK构建后缀树的算法，挺不好理解。努力写下自己的理解。

I 基本思想

构建后缀树的基本思想：假设 T[0..i-1] 的后缀树已经建好了，那么在 T[0..i-1] 的每个后缀 T[0..i-1], T[1..i-1] .. T[j..i-1] .. T[i-1..i-1],””(空字符串)，的后面加上字符 T[i] 就可以得到 T[0..i] 的后缀树了。注意，有一个底节点“bottom vertex”和根连接，这个节点和根连接的边对应空字符串。

若T[0...i-1]已经构建好，这个树上的节点分为三种：叶节点，显式节点，隐式节点。从根到每个节点的所有边上的字符组成一个字符串，我们就说每个节点对应一个后缀字符串，其中根节点对应的是空字符串；反过来就是每个后缀或者每个字串在树上都对应若干条边，但是一个后缀的结束节点可能是显示节点或叶节点，也可能是隐式节点；

具体到 “将 T[i] 加到后缀T[j..i-1]” 的这个过程，则有可能遇到三种扩展情况：

扩展情况1.在后缀树中，T[j..i-1] 停在了叶节点上。这种情况下，只需要把 T[i] 加到该叶节点的入边上即可。

扩展情况2.在后缀树中，T[j..i-1] 的后面紧跟着的字符的集合 {a,b,c ... } 中不包含 T[i]。两种情况：1)T[j...i-1]在显式节点结束，这个节点的每个子树的边对应的字符串都不以T[i]开始；2)T[j...i-1]在隐式节点结束，这个节点所在边的下一个字符不是T[i]。这种情况下，在 T[j..i-1] 的后面加上树叶 T[i](可能需要把隐式节点变换成显式节点)。

扩展情况3.后缀树中已经有 T[j..i] 了。这种情况下，我们什么都不用做。

例如，构建BOOB的后缀树，若BOO的后缀树已经构建完，

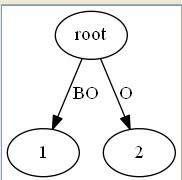
                                                                                                                                            BOO后缀树

BOO的后缀包括T[0..2]=BOO, T[1..2]=OO, T[2..2]=O, “”(空字符串)。

T[3]=“B”，依次将T[3]添加到BOO的每个后缀上：

i)T[3]添加到T[0..2],T[0..2]=“BOO“是在叶节点结束，按第一种情况添加。

ii) T[3]添加到T[1..2],T[1..2]=“OO”是在叶节点结束，按第一种情况添加。

iii) T[3]添加到T[2..2],T[2..2]=“O”是在隐式节点结束，这个隐式节点在根节点到2号节点的边上，它后面的字符是”O”,不是”B”（见上图），按第二种情况添加。这时要把隐式节点变为显式，然后添加一个叶节点。

iv) T[3]添加到空字符串。空字符串是在根节点结束，根节点是显式节点，它有两个边，其中第一个边的首字符是”B”,和T[3]一样（见上图），所以这种添加情况就是第三者情况。

添加完T[3]到每个后缀后，还没有结束，这时如果在后缀树上找后缀”B”,就不好找了。我们在字符串后面添加一个特殊字符，一般是”$”或者”#”,也就是BOOB$，我们在把这个特殊字符”$”添加到后缀树上。

这样，搜索后缀时，只要搜索到字符串以”$”结束，就表示搜索到了一个后缀。找后缀B，就是”root->5->6”。

 

II 叶节点的特性

 

后缀树T[0..i-1]如果有n个叶节点，那么这些叶节点必然是对应后缀T[0..i-1],T[1..i-1],…,T[n-1..i-1]。因为如果T[j..i-1]不是在叶节点结束(是显式节点或者隐式节点)，那么T[j+1..i-1]也不是在叶节点结束。如果T[j..i-1]不是在叶节点，假设T[j+1..i-1]=s,则T[j..i-1]=as, a是一个字符；那么必然至少有as+s1(s1至少是一个字符)是一个后缀，那么s+s1也是一个后缀，我们知道一个字符子串在后缀树上的路径（从根开始）有且只有一条，字串s+s1’的路径，肯定是找到s后再继续找s1’的路径，如果s是叶节点，就不能继续找到s1’了，也就是s+s1不是后缀，这显然不正确。所以s不可能是叶节点，也就是T[j+1..i-1]不是叶节点。

 

如果T[j..i-1]是叶节点，添加的方法就是把T[i]加到边上。在以后的扩充后缀树的过程中，这个叶节点永远是叶节点，只是可能会把边上的某个隐式节点变为显式节点。因此我们在增加一个叶节点后，就让这个叶节点的入边的结束字符指向最后一个字符。举例理解。我们要构建BOOKE的后缀树，从构建的过程中我们发现每次新加入的叶节点(节点1，节点2，节点4，节点5，节点6)，一直到整个树构建完，他们都是叶节点，叶节点的特点就是入边的最后一个字符一定指向整个字符串的最后一个字符，所以从一开始每个叶节点的入边的最后一个字符就指向整个字符串的最后一个字符，每次扩充后缀树时都不需要扩充叶节点的入边了。

                          

             步骤1                                                        步骤2                                                     步骤3

          

                             步骤4                                                                          步骤5

 

III. 对非叶节点的扩充

 

既然我们扩充时不需要关心叶节点，我们就需要找到第一个非叶节点，从这个节点对应的后缀开始扩充。把第一个非叶节点称为激活节点。比如，T[0..i-1]已经构建，若有n个叶节点，那么第一个非叶节点，也就是激活节点就是T[n..i-1]对应的节点，我们添加只要从激活节点开始。如果所有非空后缀都是叶节点，那么根节点就是激活节点。添加时如果遇到上面所说的扩展情况3，则添加结束，我们把结束时的后缀对应的节点称为结束节点。

 

结束情况1：如果扩展时一直是上面扩展情况2，那么最后是将T[i]添加到根节点后，根节点是结束节点；

结束情况2：如果在添加T[i]到T[k…i-1]时遇到扩展情况3，那么添加T[i]到T[0…i-1]各个后缀的过程就结束了，T[k…i-1]对应的节点就是结束节点。

 

分析上面两种情况的结束节点，我们可以知道比结束节点对应后缀长的的后缀肯定都是在叶节点结束。假设我们添加T[i]到T[0..i-1], T[0..i-1]有n个叶节点，那么添加从后缀T[n..i-1]开始，假设后缀T[k..i-1]对应的节点是结束节点。因为叶节点添加之后还是叶节点，那么新后缀T[0..i],T[1..i],…,T[n-1..i]一定在叶节点结束；新后缀T[n…i]到T[k-1….i]的结束节点一定是按照上面的添加情况2来添加的，而新添加的节点也一定是叶节点，所以新后缀T[n+1..i]到T[k-1..i]也都是在叶节点结束。T[k..i]就是添加T[i+1]到T[0..i]后缀树上时的激活节点。

 

IV.寻找下一个更短后缀的方法

我们在生成后缀树T[0..i]时，是需要找到每一个T[0..i-1]的不在叶节点结束的后缀，如果我们已经添加完T[p..i-1],我们需要寻找下一个后缀T[p+1..i-1]。所谓寻找T[p+1..i-1]就是找到T[p+1..i-1]后缀的结束节点，因为我们最终是要把T[i]添加到后缀的结束节点上（这个结束节点是一个后缀的结束节点，任何一个后缀，从根节点开始，总是在一个节点结束。不是上面所说的某一轮添加过程中的结束节点），如果在显式节点结束，就是这个显式节点；如果在隐式节点结束，就是隐式节点所在边的开始节点。

i寻找方法一:从根节点开始寻找

在寻找的过程中，我们需要运用skip/count的技巧。

假设我们要从根开始寻找后缀T[p..i-1],我们只有找到根节点下首字符为T[p]的边，假设为E1,后缀T[p..i-1]肯定沿着这条边往下寻找。假设边E1对应字符串长度为length(E1),如果length(T[p..i-1])<=length(E1),那么后缀T[p..i-1]的结束节点就是边E1上的隐式节点或者是E1的节点；如果length(T[p..i-1])>length(E1),假设E1的另一个节点是V1,接着在V1的出边中寻找首字符是T[length(E1)]的边，后缀T[p..i-1]肯定继续沿着这条边往下寻找。类似的方法一直找到后缀T[p..i-1]。

 

ii.寻找方法二：利用后缀链接

什么是后缀链接?

通俗说就是从一个字符串的结束节点,指向比它短一个字符的字符串的节点。

如果aS是一个字符串，a是一个字符，S是一个子串（可以是空串），若aS在一个显式节点结束（假设为v1），则S子串也是在一个后缀节点结束（假设为v2），则从v1指向v2的指针称为后缀链接。

 上面的描述中隐含一个事实：如果aS字符串在一个显式节点结束，那么S字符串也一定在一个显式节点结束。理解这个事实。既然aS在一个显式节点结束，那么一定存在后缀aS+S1,以及aS+S2,其中S1和S2是字符串或者单个字符，并且它们不相同其不为空，那么一定存在后缀S+S1以及S+S2。从根节点出发我们找到字符串S对应的节点，这样的路径存在且唯一，如果这个节点是叶节点，那么就不可能存在后缀S+S1或者S+S2；如果这个节点是隐式节点，我们搜索S+S1或者S+S2,都一定先搜索到S然后向下继续搜索，S是隐式节点，S之后就不可能跟不同的字符来组成不同的字符串，也就是以S开头的后缀只能有一个，而现在是两个，所以不可能是隐式节点。所以我们可以知道S对应的节点一定是显式的。

 从上面的理解我们可以知道：

创建后缀树过程中，如果在第i阶段，第j步扩展中，创建了一个对应字符串为aS的显式节点，那么要么存在一个对应字符串为S的显式节点；要么在下一步(j+1)创建一个对应字符串为S的显式节点。aS对应的节点到S对应的节点就建立一个后缀链接。

因此任何一个显式节点（除根节点）都有后缀链接，通过后缀链接我们就可以快速的寻找下一个更短的字符串。

 

Reference：

http://www.if-yu.info/2010/10/3/suffix-tree.html

http://blog.163.com/lazy_p/blog/static/13510721620108139476816/（三鲜翻译文章）原文在这里：http://marknelson.us/1996/08/01/suffix-trees/

 http://www.allisons.org/ll/AlgDS/Tree/Suffix/