图的 Prim算法和Dijkstra算法
用矩阵形式实现图的两个算法
1) 无向图中,使用Prim算法,构建最小生成树
2) 有向图中,使用DijKstra算法,得到单源最短路径
首先构建一下图,这里是用矩阵实现的
Graph类简述:
numVertex 是图中当前的节点数
numEdge 是图中当前的边数
maxNumVertex 表示未自增长前的矩阵中节点最大值
maxNumEdge 表示未自增长前的矩阵中边最大值
使用一维数组NodeList[]来存储节点信息
使用一维数组AdjMatrix[]来存放邻接表 AdjMatrix[I * maxNumVertex + j] 表示i号节点到j节点的有向路径的长度如下图
设MAX为9999 初始化时两点表示不可达
设MAX_EDGETYPE为9999 表示边的无穷大 也表示不可达
主要代码
Graph.hpp
#include <iostream>
using namespace std;
#define DEFAULT_VERTEX_NUM 5
#define MAX 99999
#define MAX_EDGETYPE 99999
template<class VertexType,class EdgeType>
class Graph{
VertexType *NodeList; //保存顶点数据的一位数组
EdgeType *AdjMatrix; //保存邻接矩阵的一维数组,邻接矩阵
//AdjMatrix[i*NumVertex + j] ,表示
//i顶点到j顶点方向,数值表示路径长度
int currentNode; //指着当前的节点
int numEdge; //图当前的边数
int maxNumEdge; //图的最大边数
int numVertex; //图当前的顶点数
int maxNumVertex; //图最大的顶点数
public:
Graph(int );
~Graph();
int GetNumVertex(){return numVertex;}
VertexType InsertVertex(const VertexType& ); //插入一个节点
int RemoveVertex(const VertexType& ); //删除一个节点
EdgeType InsertEdge(int i,int j,EdgeType weight); //从i向j插入一条权重为weight的边
int RemoveEdge(int i ,int j); //移除i向j的边
void ExpandSize(); //用于动态自增长,节点数翻倍、同时边数相应翻两倍
/*传入一个初始的的顶点,进行Prim算法来构建最小生成树构建方式用一维数组表示 如PrimTree[i*numVertex + j],
*由于Graph类设计的时候考虑到了有向图的情况,但是在本算法中并不使用有向图,所以上面的PrimTree[i*numVertex + j]
*也等同于PrimTree[j*numVertex + i]. 本函数返回的就是这样的一个数组*/
EdgeType *Prim(VertexType startVertexValue);
EdgeType *Dijkstra(VertexType startVertexValue);
void Cout();
};
//测试输出
template<class VertexType,class EdgeType>
void Graph<VertexType, EdgeType>::Cout(){
cout << "NodeList 数组索引:\n";
cout <<" i\\j";
for(int i = 0;i < numVertex;i++)
cout << "\t" << i << " ";
int cntLine = 0; //列计数
int cntRow = 0; //行计数
//cout << "\n邻接矩阵数据:\n";
cout << endl;
for(int i = 0;i < maxNumEdge;i++){
if( i % maxNumVertex == 0 && cntRow < numVertex )
cout << "\t" << cntRow++;
if(cntRow == numVertex && cntLine == numVertex )
break;
if(cntLine++ < numVertex && cntRow <= numVertex)
cout << "\t" << AdjMatrix[i] ;
if( (i + 1) % maxNumVertex == 0){ //每行遍历结束换行
cout << endl;
cntLine = 0;
}
}
cout << endl;
cout << "各节点的值: \n";
for(int i = 0;i < numVertex;i++)
cout << NodeList[i] << " ";
cout << "\n\n";
}
//动态自增长
template<class VertexType,class EdgeType>
void Graph<VertexType, EdgeType>::ExpandSize(){
//复制所有节点数组到扩容后的NodeList
VertexType *tempNodeList = NodeList;
int originMaxNumVertex = maxNumVertex;
maxNumVertex <<= 1;
NodeList = new VertexType[maxNumVertex];
for(int i = 0;i < (maxNumVertex >> 1);i++)
NodeList[i] = tempNodeList[i];
delete []tempNodeList;
//复制邻接边数组AdjMatrix
EdgeType *tempAdjMatrix = AdjMatrix;
// int originMaxNumEdge = maxNumEdge;
maxNumEdge = maxNumVertex * maxNumVertex;
AdjMatrix = new EdgeType[maxNumEdge];
for(int i = 0;i < originMaxNumVertex;i++)
for(int j = 0;j < originMaxNumVertex;j++)
AdjMatrix[maxNumVertex * i + j] = tempAdjMatrix[originMaxNumVertex * i + j];
//未知变量都赋为MAX表示不可达,修改对角线元素为0
for(int i = 0;i < maxNumVertex;i++)
for(int j = 0;j < maxNumVertex;j++){
if(!(i < originMaxNumVertex && j < originMaxNumVertex)){
AdjMatrix[maxNumVertex * i + j] = MAX;
}
}
for(int i = originMaxNumVertex;i < maxNumVertex;i++){
AdjMatrix[maxNumVertex * i + i] = 0;
}
delete []tempAdjMatrix;
}
template<class VertexType,class EdgeType>
VertexType Graph<VertexType, EdgeType>::InsertVertex(const VertexType& newVertexValue){
if(numVertex == maxNumVertex)
ExpandSize();
NodeList[numVertex++] = newVertexValue;
return newVertexValue;
}
template<class VertexType,class EdgeType>
int Graph<VertexType, EdgeType>::RemoveVertex(const VertexType& vertexValue){
if(numVertex == 0)
return -1; //没有找到
else{
int pos = 0;
for(;pos < numVertex;pos++){
if(NodeList[pos] == vertexValue)
break;
}
if(pos == numVertex)
return -1; //没有找到
for(int i = pos;i < numVertex;i++){
NodeList[i] = NodeList[i + 1];
}
for(int i = 0;i < maxNumVertex - 1;i++)
for(int j = 0;j < maxNumVertex - 1;j++){
int x = j >= pos ? j + 1 : j;
int y = i >= pos ? i + 1 : i;
AdjMatrix[maxNumVertex * i + j] = AdjMatrix[maxNumVertex * y + x];
}
return --numVertex;
}
}
template<class VertexType,class EdgeType>
EdgeType Graph<VertexType, EdgeType>::InsertEdge(int i,int j,EdgeType weight){
if(i < maxNumVertex && j < maxNumVertex && i != j)
AdjMatrix[maxNumVertex * i + j] = weight;
return weight;
}
template<class VertexType,class EdgeType>
int Graph<VertexType, EdgeType>::RemoveEdge(int i,int j){
if(i < maxNumVertex && j < maxNumVertex && i != j){
AdjMatrix[maxNumVertex * i + j] = MAX;
numEdge--;
return numEdge;
}else
return -1;
}
template<class VertexType,class EdgeType>
Graph<VertexType,EdgeType>::Graph(int maxVertexSize = DEFAULT_VERTEX_NUM){
numVertex = 0;numEdge = 0;currentNode = 0;
maxNumVertex = maxVertexSize > DEFAULT_VERTEX_NUM ? maxVertexSize : DEFAULT_VERTEX_NUM;
maxNumEdge = maxNumVertex * maxNumVertex;
AdjMatrix = new EdgeType[maxNumEdge];
NodeList = new VertexType[maxNumVertex];
// 对角线顶点初始化为0,非对角线初始为MAX表示不可达
for(int i = 0;i < maxNumEdge;i++)
AdjMatrix[i] = MAX;
for(int i = 0;i < maxNumVertex;i++)
AdjMatrix[i + maxNumVertex * i] = 0;
}
template<class VertexType,class EdgeType>
Graph<VertexType,EdgeType>::~Graph(){
delete []AdjMatrix;
delete []NodeList;
}
template<class VertexType,class EdgeType>
EdgeType* Graph<VertexType,EdgeType>::Prim(VertexType startVertexValue){
//初始化PrimTree所有点之间都不可达
EdgeType *PrimTree = new EdgeType[numVertex * numVertex];
for(int i = 0;i < numVertex;i++)
for(int j = 0;j < numVertex;j++){
PrimTree[i * numVertex + j] = MAX_EDGETYPE;
}
int startPos = -1;
for(int i = 0;i < numVertex;i++){
if(NodeList[i] == startVertexValue){
startPos = i;
break;
}
}
if(startPos == -1) //如果没有找到,就返回NULL
return NULL;
//isChosen数组记录顶点i是否被取出
bool *isChosen = new bool[numVertex];
for(int i = 0;i < numVertex;i++)
isChosen[i] = false;
//选出指定的头结点,放入顶点集U,startPos是起始顶点
isChosen[startPos] = true;
int lastPos = startPos; //作图的时候保留每一次绘制边的起始顶点
int nextPos; //作图的时候保留每一次绘制边的终止顶点
int newPos = startPos; //新加入顶点的定位
for(int i = 0;i < numVertex - 1;i++){ //把所有节点都包括进来,前提是一副连通图
EdgeType min = MAX_EDGETYPE;
/* 找到在U-V中仍未选入的第一个顶点
*每一次有新节点加入的时候都要定位在新节点,首先由到新节点的权值最小,选择下一个加入的顶点*/
for(int j = 0;j < numVertex;j++){
//如果某个顶点还未被选走
if(!isChosen[j]){
EdgeType weight = AdjMatrix[newPos * maxNumVertex + j] < AdjMatrix[j * maxNumVertex + newPos] ?
AdjMatrix[newPos * maxNumVertex + j] : AdjMatrix[j * maxNumVertex + newPos];
if(weight < min){
min = weight;
nextPos = j;
}
}
}
//还原min的初始值
min = MAX_EDGETYPE;
for(int j = 0;j < numVertex;j++){
if(isChosen[j]){ //在已经被选走的顶点中找到距离上面未加入顶点权值最小的顶点,作为画边的起始顶点
EdgeType weight = AdjMatrix[j * maxNumVertex + nextPos] < AdjMatrix[nextPos * maxNumVertex + j] ?
AdjMatrix[j * maxNumVertex + nextPos] : AdjMatrix[nextPos * maxNumVertex + j];
if(weight < min){
min = weight;
lastPos = j;
}
}
}
PrimTree[lastPos * numVertex + nextPos] = min;
isChosen[nextPos] = true;
newPos = nextPos; //newPos 每次都指向刚刚新加入的顶点
}
return PrimTree;
}
template<class VertexType,class EdgeType>
EdgeType* Graph<VertexType,EdgeType>::Dijkstra(VertexType startVertexValue){
EdgeType *DijkstraPath = new EdgeType[numVertex];
int startPos = -1;
for(int i = 0;i < numVertex;i++){
if(NodeList[i] == startVertexValue){
startPos = i;
break;
}
}
if(startPos == -1) //如果没有找到,就返回NULL
return NULL;
//记录源点到各顶点的最短路径
for(int i = 0;i < numVertex;i++)
DijkstraPath[i] = AdjMatrix[startPos * maxNumVertex + i];
//isChosen数组记录顶点i是否被取出
bool *isChosen = new bool[numVertex];
for(int i = 0;i < numVertex;i++)
isChosen[i] = false;
//初始顶点加入
isChosen[startPos] = true;
EdgeType min;
int nextPos;
//修改startPos有向可达的图DijkstraGraph[]
for(int i = 0;i < numVertex - 1;i++){
min = MAX_EDGETYPE;
for(int j = 0;j < numVertex;j++){
EdgeType weight = AdjMatrix[startPos * maxNumVertex + j];
if(!isChosen[j]){
if(weight < min){
min = weight;
nextPos = j;
}
}
}
//取走nextPos
isChosen[nextPos] = true;
//每次有新的点加入就更新DijkstraGraph[]
for(int j = 0;j < numVertex;j++){
EdgeType D_startToNext = AdjMatrix[startPos * numVertex + nextPos];
EdgeType D_NextToJ = AdjMatrix[nextPos * numVertex + j];
EdgeType D_startToJ = AdjMatrix[startPos * numVertex + j];
if(D_startToNext + D_NextToJ < D_startToJ)
DijkstraPath[j] = D_startToNext + D_NextToJ;
}
}
return DijkstraPath;
}
一. 先做了基本成员函数的正确性验证:
1.插入和删除节点
InsertVertex(const EdgeType&) 和 RemoveVertex(const EdgeType &)
2. 插入和删除边
InsertEdge(int i,int j,EdgeType weight) 和 RemoveEdge(int i,int j)
3 增加节点的时候动态增长
ExpandSize()
成功的在Insert的时候动态增长了原先的节点总数,和邻接表AdjMatrix的规模
测试代码:
int main(){
Graph<int,int> g;
for(int i = 0;i < 6;i++){
g.InsertVertex(i);
}
g.InsertEdge(2,3,23);
g.InsertEdge(2,4,24);
g.InsertEdge(3,4,34);
g.InsertEdge(1,5,15);
g.Cout();
g.RemoveVertex(2);
g.Cout();
return 0;
}
得到输出:
1)成功的用InsertVertex() 和InsertEdge()函数插入了新的节点和新的边
2)删除了节点值为int 2 的点,并且对原先的两个数组进行了重购索引 2 之后的节点填充了NodeList[]和AdjMatrix[]中原来[2]的位置
二. Prim算法实现简述:
Prim函数代码:
template<class VertexType,class EdgeType>
EdgeType* Graph<VertexType,EdgeType>::Prim(VertexType startVertexValue){
//初始化PrimTree所有点之间都不可达
EdgeType *PrimTree = new EdgeType[numVertex * numVertex];
for(int i = 0;i < numVertex;i++)
for(int j = 0;j < numVertex;j++){
PrimTree[i * numVertex + j] = MAX_EDGETYPE;
}
int startPos = -1;
for(int i = 0;i < numVertex;i++){
if(NodeList[i] == startVertexValue){
startPos = i;
break;
}
}
if(startPos == -1) //如果没有找到,就返回NULL
return NULL;
//isChosen数组记录顶点i是否被取出
bool *isChosen = new bool[numVertex];
for(int i = 0;i < numVertex;i++)
isChosen[i] = false;
//选出指定的头结点,放入顶点集U,startPos是起始顶点
isChosen[startPos] = true;
int lastPos = startPos; //作图的时候保留每一次绘制边的起始顶点
int nextPos; //作图的时候保留每一次绘制边的终止顶点
int newPos = startPos; //新加入顶点的定位
for(int i = 0;i < numVertex - 1;i++){ //把所有节点都包括进来,前提是一副连通图
EdgeType min = MAX_EDGETYPE;
/* 找到在U-V中仍未选入的第一个顶点
*每一次有新节点加入的时候都要定位在新节点,首先由到新节点的权值最小,选择下一个加入的顶点*/
for(int j = 0;j < numVertex;j++){
//如果某个顶点还未被选走
if(!isChosen[j]){
EdgeType weight = AdjMatrix[newPos * maxNumVertex + j] < AdjMatrix[j * maxNumVertex + newPos] ?
AdjMatrix[newPos * maxNumVertex + j] : AdjMatrix[j * maxNumVertex + newPos];
if(weight < min){
min = weight;
nextPos = j;
}
}
}
//还原min的初始值
min = MAX_EDGETYPE;
for(int j = 0;j < numVertex;j++){
if(isChosen[j]){ //在已经被选走的顶点中找到距离上面未加入顶点权值最小的顶点,作为画边的起始顶点
EdgeType weight = AdjMatrix[j * maxNumVertex + nextPos] < AdjMatrix[nextPos * maxNumVertex + j] ?
AdjMatrix[j * maxNumVertex + nextPos] : AdjMatrix[nextPos * maxNumVertex + j];
if(weight < min){
min = weight;
lastPos = j;
}
}
}
PrimTree[lastPos * numVertex + nextPos] = min;
isChosen[nextPos] = true;
newPos = nextPos; //newPos 每次都指向刚刚新加入的顶点
}
return PrimTree;
}
步骤:
1)由传入的顶点值参数找到顶点startPos
2)为了绘制边,需要lastPos记录边起始顶点,nextPos 记录边终止顶点
3)循环遍历所有顶点,直到所有顶点加入到已选取集V为止
4)每次选取待加入顶点时,未加入V的顶点都需要通过和前一次循环刚加入的新顶点newPos,以newPos为起始点进行两个节点之间的权值比较选取权值最小一条边,该边的终点的顶点索引就是nextPos
5)得到的nextPos还必须和已选取集V中所有顶点比较,选择在这之中权值最小的边,得到一个lastPos为要新加入的边起始点,nextPos为该边的终点,在PrimTree中绘制
PrimTree[lastPos * numVertex + nextPos] ,同时把nextPos加入已选取集V
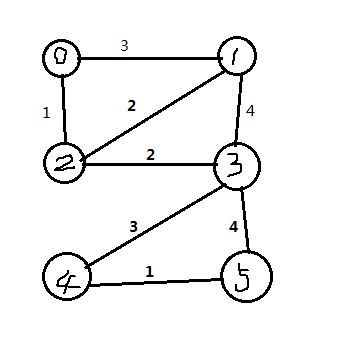
原始图:
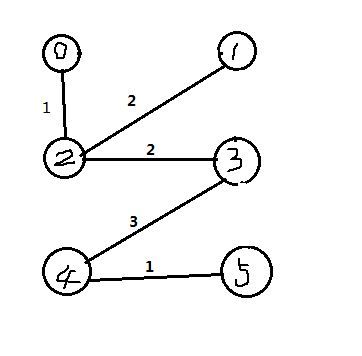
最小生成树的图:
测试代码main.cpp
int main(){
Graph<int,int> g;
for(int i = 0;i < 6;i++){
g.InsertVertex(i);
}
//初始化图
g.InsertEdge(0,1,3);
g.InsertEdge(0,2,1);
g.InsertEdge(1,2,2);
g.InsertEdge(1,3,4);
g.InsertEdge(2,3,2);
g.InsertEdge(3,4,3);
g.InsertEdge(3,5,4);
g.InsertEdge(4,5,1);
cout << "原始图:" << endl;
g.Cout();
cout << "\n\n最小生成树的图: " << endl;
//Prim构建最小生成树
int numVertex = g.GetNumVertex();
int *PrimTree = g.Prim(0);
for(int i = 0;i < numVertex;i++)
cout << "\t" << i;
cout << endl;
for(int i = 0,cntLine = 0;i < numVertex;i++){
cout << "" << cntLine++;
for(int j = 0;j < numVertex;j++){
cout << "\t" << PrimTree[i * numVertex + j];
}
cout << endl;
}
cout << endl;
return 0;
}
测试输出:(使用数组实现图,因为设计Graph类的时候考虑了有向性,但是在实现Prim算法的时候没有用到方向
所以在数组中AdjMatrix[i][j] 和 AdjMatrix[j][i] 二者是相同的,二选一即可,99999是MAX值表示不可达!
三. Dijkstra算法实现简述
Dijkstra代码:
template<class VertexType,class EdgeType>
EdgeType* Graph<VertexType,EdgeType>::Dijkstra(VertexType startVertexValue){
EdgeType *DijkstraPath = new EdgeType[numVertex];
int startPos = -1;
for(int i = 0;i < numVertex;i++){
if(NodeList[i] == startVertexValue){
startPos = i;
break;
}
}
if(startPos == -1) //如果没有找到,就返回NULL
return NULL;
//记录源点到各顶点的最短路径
for(int i = 0;i < numVertex;i++)
DijkstraPath[i] = AdjMatrix[startPos * maxNumVertex + i];
//isChosen数组记录顶点i是否被取出
bool *isChosen = new bool[numVertex];
for(int i = 0;i < numVertex;i++)
isChosen[i] = false;
//初始顶点加入
isChosen[startPos] = true;
EdgeType min;
int nextPos;
//修改startPos有向可达的图DijkstraGraph[]
for(int i = 0;i < numVertex - 1;i++){
min = MAX_EDGETYPE;
for(int j = 0;j < numVertex;j++){
EdgeType weight = AdjMatrix[startPos * maxNumVertex + j];
if(!isChosen[j]){
if(weight < min){
min = weight;
nextPos = j;
}
}
}
//取走nextPos
isChosen[nextPos] = true;
//每次有新的点加入就更新DijkstraGraph[]
for(int j = 0;j < numVertex;j++){
EdgeType D_startToNext = AdjMatrix[startPos * numVertex + nextPos];
EdgeType D_NextToJ = AdjMatrix[nextPos * numVertex + j];
EdgeType D_startToJ = AdjMatrix[startPos * numVertex + j];
if(D_startToNext + D_NextToJ < D_startToJ)
DijkstraPath[j] = D_startToNext + D_NextToJ;
}
}
return DijkstraPath;
}
步骤:
1)由传入的顶点值参数找到顶点startPos
2)先把顶点startPos可达的顶点和权值赋值给DijkstraPath[]
3)循环遍历所有顶点,直到所有顶点加入到已选取集V为止
4)每次选取待加入顶点时,未加入V的顶点都需要通过比较初始顶点到达新顶点的路径长度,选择最小路径长度的新顶点,作为下一个要处理的顶点nextPos
5) 得到的nextPos后,重新比较开始顶点到nextPos顶点:D_startToNext ; nextPos顶点到j顶点:D_NextToJ 以及 开始顶点startPos到j D_startToJ的路径长度比较,如果由于新插入的点,即nextPos顶点使得起始顶点startPos到顶点j的路径变短,那么就重新对startPos到j的Dijkstra[j] 重新赋值。
原始图:
测试代码:
/******************Dijkstra算法测试********************************/
int main(){
Graph<int,int> g;
for(int i = 0;i < 5;i++){
g.InsertVertex(i);
}
//初始化图
g.InsertEdge(0,1,10);
g.InsertEdge(1,2,50);
g.InsertEdge(3,2,20);
g.InsertEdge(3,4,30);
g.InsertEdge(0,3,30);
g.InsertEdge(2,4,10);
g.InsertEdge(0,4,100);
cout << "原始有向图:" << endl;
g.Cout();
int startVertexValue = 0;
int numVertex = g.GetNumVertex();
int *DijkstraPath = g.Dijkstra(startVertexValue);
cout << endl << "由startPos的Dijkstra有向可达路径图:\n";
cout << "\t";
for(int i = 0;i < numVertex;i++)
cout << "\t" << i;
cout << endl;
cout << "\t" << startVertexValue;
for(int i = 0;i < numVertex;i++)
cout << "\t" <<DijkstraPath[i] ;
return 0;
}
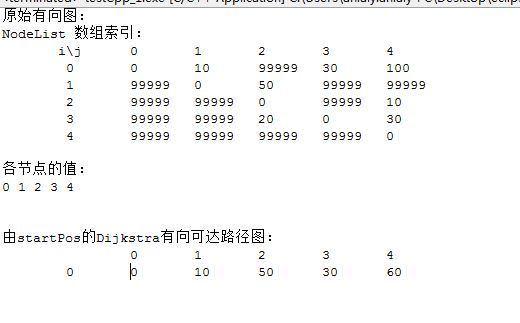
测试输出:
上图中,0是起始顶点,即startPos 到顶点1 2 3 4 的路径长度分别是10 、 50、30、60