《STL源码剖析》 笔记2
算法注意
adjacent_difference,partial_sum
互为逆运算
equal
如果2个序列在[first,last)内相等,返回true;
如果第2个序列元素较多,多出来的元素不考虑;
因此;保证2个序列完全相等的方法:必须先判断元素个数是否相同
注意
比较两个序列完全相等时:必须保证二者长度相等:
if(vec1.size()==vec2.size()&&equal(vec1.begin(),bec1.end(),vec2.begin()))
fill,fill_n
覆盖写入:更改新值
容易出现的问题 操作区间超出容器的大小
如果n超越了容器的大小,结果不可预期:
原因:每次迭代是覆写操作
int a[3]={1,2,3};
vector<int>iv(a,a+3);
fill_n(iv.begin(),5,7);
解决:使用inserter()产生插入能力的迭代器
fill_n(inserter(iv.begin()),5,7);//7 7 7 7 7 1 2 3
iter_swap与swap对比
用法:
iter_swap(iv1.begin(),iv2.begin());
swap(*iv1.begin(),*iv2.begin());
lexicographical_compare
注意:
默认小于比较(<)时 返回true
如果第1个序列元素小,返回true,否则false;
如果到达last1,未到达last2,返回true;
如果为到达last1,到达last2,返回false;
同时到时last1,last2(完全匹配),返回false
实现 char版本
bool lexicographical_compare(char *first1,char*last1,char*first2,char*last2,funtypecomp)// 函数指针或函数对象
{
for(:first1!=last1&&first2!=last2;++first1,++first2)
{
if(comp(*first1,*first2))return true;
if(!comp(*first1,*first2))return false;
}
returnfirst1==last1&&first2!=last2;
}
STL源码实现

原生指针版本
mismatch
返回迭代器:分别执行两序列的不匹配点
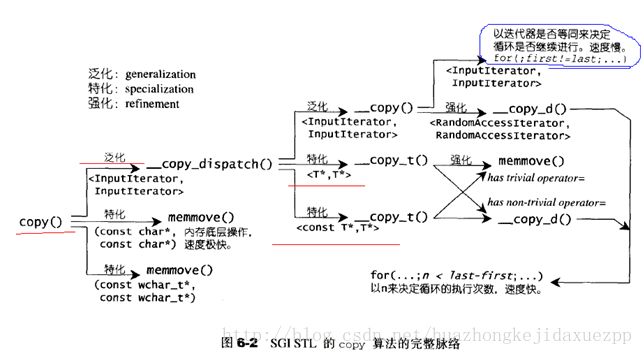
copy注意
问题
区域重叠时,可能会出错:
1- 若根据迭代器的特性调用memmove()执行-----不会出错
例如vector,迭代器是个原生指针,导致copy算法一memmove()执行实际的复制操作。
因为memmove()现将整个输入区间的内容复制下来,没有覆盖危险
2-否则出错。deque,因为copy算法不再使用memmove执行实际复制操作
解决
由于copy不能直接将元素插入空容器,可以使用如下方法:
1, 序列容器的insert成员函数;
2, 或者copy算法搭配insert_iterator
注意:
1,对原生指针const char*,const wchar_t*---内存直接拷贝 mommove()
2,特化版本:
input迭代器-----速度慢 for循环中使用迭代器是否等同(first!=last)决定是否继续
随机迭代器-------速度快 for循环中使用n决定是否继续(n=last-first,n>0;n--)STL源码如下:
copy_backward
逆方向复制;
同样的问题:输入区间的起点与输入区间重叠时,可能出错:
要看调用的copy版本而定,即由迭代器的特性决定。
set算法
集合
![]()
算法:
1while(first1~=last1&&fitst2~=last2)
2,加入较小者,指针前进,相等时,加入一个
3,尾部处理 copy(first2,last2,copy(fist1,last1,result))
![]()
算法:
1while(first1~=last1&&fitst2~=last2)
2,较小者指针前进,相等时,加入
![]()
算法:
1while(first1~=last1&&fitst2~=last2)
2,较小者为*S1,加入,指针前进,否则指针S2前进或都前进(相等时)
3,尾部处理 copy(first1,last1,result)
![]()
算法:
1while(first1~=last1&&fitst2~=last2)
2,较小者加入,仅相等时不加入
3,尾部处理 copy(first2,last2,copy(fist1,last1,result))
includes
必须有序;
时间复杂度:n^2
merge
注意两点:
必须有序;
类似inplace_merge,是稳定操作,如果2个序列有等同元素,第1个序列的元素位于第2个序列元素之前。
inplace_merge:
内存空间
分配失败---无buffer时合并;
否则在有暂时缓冲区的情况下进行。
有缓冲区时----
(1)缓冲区足够安装序列一,
序列一放入缓冲区,merge()合并序列二;
(2)如果缓冲区足够安装序列二,
序列二放入缓冲区,merge()合并序列一;
(3)不足安置任何一个序列
选出序列较长的一个,
递归分割,让处理长度减半,看看能否容纳于缓冲区mergesort
分而治之的思想:
将区间对半分割,左右各自排序;
使用inplace_merge重新组合为一个有序序列,对半分割的操作可以递归进行,直到每一小段的长度为0/1复杂度:O(N*logN)
因为要借助额外的内存,内存间移动也耗时间,所以效率比不上快排。
优点:实现简单+概念简单remove,remove_if,remove_copy
注意:残余元素
remove_copy注意:
新旧容器可以重叠,但若对新容器实际给值时,超越了
旧容器的大小,参数未知结果。
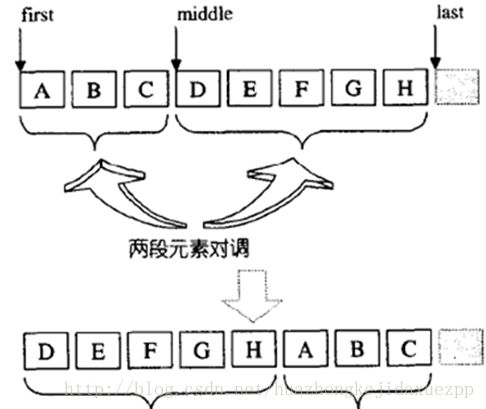
rotate
原理:unique
对排序后序列使用;
使用earse删除残余数据二分搜索的版本
必须有序序列使用;
lower_bound
upper_bound
binary_search【lower_bound实现】源代码实现:
n个无序数中选取最小的k个数(n>k)
partial_sort 堆

《剑指offer》:使用set 实现
typedef multiset<int,greater<omt> >::iterator setiterator;
void getleastnumbers(const vector<int>&data,intset& leastnumbers,int k)
{
leastnumbers.clear();
if(k<1||data.size()<k)
return;
vector<int>::const_iterator iter=data.begin();
for(;iter!=data.end();++iter)
{
if(leastnumbers.size()<k)
leastnumbers.insert(*iter);
else
{
setitetator itergreatest=leastnumbers.begin();
if(*iter<*(leastnumbers.begin()))
{
leastnumbers.erase(itergreatest);
leastnumbers.insert(*iter);
}
}
}
}
sort
STL的sort算法思想:
1,数据量大时,采用快排,分段递归排序;
2,一旦分段后的数据量小于一个阈值(16),为了避免快排的递归带来的额外负荷,改用插入排序;
3,如果递归层次过深,改用堆排序