位运算状态压缩——跳棋

Description

一个如下的6 x 6的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列只有一个，每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。 
上面的布局可以用序列2 4 6 1 3 5来描述，第i个数字表示在第i行的相应位置有一个棋子，如下： 
 

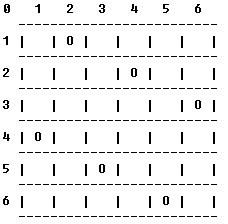
行号 1 2 3 4 5 6 
列号 2 4 6 1 3 5 
这只是跳棋放置的一个解。请编一个程序找出所有跳棋放置的解。并把它们以上面的序列方法输出。解按字典顺序排列。请输出前3个解。最后一行是解的总个数。 

特别注意: 对于更大的N(棋盘大小N x N)你的程序应当改进得更有效。不要事先计算出所有解然后只输出(或是找到一个关于它的公式），这是作弊。如果你坚持作弊，那么你登陆USACO Training的帐号将被无警告删除

Input

一个数字N (6 <= N <= 13) 表示棋盘是N x N大小的。

Output

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

Sample Input

6

Sample Output

2 4 6 1 3 5 
3 6 2 5 1 4 
4 1 5 2 6 3 
4

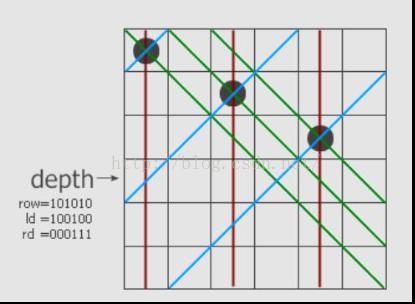
假设是6x6的棋盘，每行有6个格子，所以可以用6位的二进制数来表示该行的某个位置可用与否。1表示不可用，0表示可用。

左图中，垂直方向上第1,3,5三个格子不可用，故用二进制数101010来表示垂直方向(row)的情况。

同理，受右上往左下的斜对角线的影响，第1和第4个格子不可用，故用二进制数100100来表示右上往左下(ld)的对角线的情况。

同理，受左上往右下的斜对角线的影响，第4,5,6三个格子不可用，故用二进制数000111来表示左上往右下(rd)的对角线的情况。

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
int n,k,tot,ans[20];
int get_bits(int x){  //返回x的二进制位数 
	int cnt=0;
	while(x){
		x>>=1;cnt++;
	}
	return cnt;
}
void DFS(int row,int ld,int rd,int x){
	int p,pos;
	if(row!=k){
		pos=k&(~(row|ld|rd));
		while(pos!=0){
			p=pos&(-pos);
			pos-=p;
			ans[x]=get_bits(p); 
			DFS(row+p,(ld+p)<<1,(rd+p)>>1,x+1);
		}
	}
	else {
		if(tot<3){
			for(int i=1;i<=n;i++)
				printf("%d ",ans[i]);
			putchar('\n');
		}
		tot++;
	}
}
int main(){
	scanf("%d",&n);
	k=(1<<n)-1;
	DFS(0,0,0,1);
	printf("%d",tot);
	return 0;
} 
有点注释版:

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
int n;
int k;
int cnt=0;
int ans[10005];
void dfs(int row,int ld,int rd,int x){//row表示数值方向限制，ld表示左斜方向的限制，rd表示右斜方向的限制 
	int p,pos;
	if(x<=n){
		pos=k&(~(row|ld|rd));
		int tot=0;
		while(pos>0){
			p=pos&(-pos);
			if(cnt<3){
				//p=2^n=(10...0)2,ans[x]=n+1,
				ans[x]=log2(p)+1;
			}
			pos=pos-p;
			dfs(row+p,(ld+p)<<1,(rd+p)>>1,x+1); 
		}
	}
	else{
		cnt++;
		if(cnt<=3){
			for(int i=1;i<=n;i++)printf("%d ",ans[i]);
			cout<<endl;
		}
	}
}
int main(){
	cin>>n;
	k=(1<<n)-1;
	dfs(0,0,0,1);
	cout<<cnt;
}