poj 1390 Blocks （经典区间dp 方块消除）
|
Blocks
Description
Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold.
The corresponding picture will be as shown below: 
Figure 1 If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively. Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points. Now let's look at the picture below: 
Figure 2 The first one is OPTIMAL. Find the highest score you can get, given an initial state of this game. Input
The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.
Output
For each test case, print the case number and the highest possible score.
Sample Input 2 9 1 2 2 2 2 3 3 3 1 1 1 Sample Output Case 1: 29 Case 2: 1 Source
Liu Rujia@POJ
|
题意：
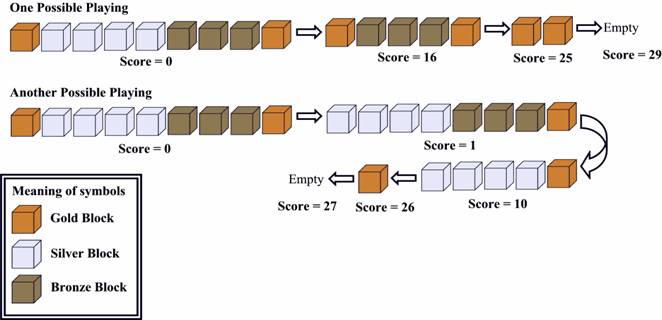
一排有颜色的方块，每次可以消除相邻的颜色相同的块，得分为方块个数的平方，消除后剩下的方块会合并，问怎样消除方块使得总得分最大。
思路：
黑书原题（p123），合并初始相邻相同的块，得到颜色数组c和对应的长度len，dp[i][j][k]表示i~j区间，与后面k个相同颜色块一起消除得分的最大值（当然k个块的颜色必须与j相同），考虑len[j]和k这一段怎么消除，有两种可能：
1.单独消除，dp[i][j][k]=dp[i][j-1][0]+(len[j]+k)^2;
2.和前面的一起消除，假设前面的一起消除的块最后一块为p，那么dp[i][j][k]=dp[i][p][k+len[j]]+dp[p+1][j-1][0]。
可以根据p和j的颜色相同以及k的范围来优化一下。
代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#define maxn 205
#define MAXN 200005
#define INF 0x3f3f3f3f
#define mod 1000000007
#define eps 1e-6
const double pi=acos(-1.0);
typedef long long ll;
using namespace std;
int n,m,ans,tot;
int a[maxn],c[maxn],len[maxn],pos[maxn],last[maxn];
int dp[205][205][205],num[maxn][maxn];
void solve()
{
int i,j,k,p;
memset(pos,0,sizeof(pos));
for(i=1;i<=tot;i++)
{
last[i]=pos[c[i]];
pos[c[i]]=i;
}
memset(num,0,sizeof(num));
for(i=tot;i>=1;i--)
{
for(j=1;j<=n;j++)
{
if(j==c[i]) num[j][i]=num[j][i+1]+len[i];
else num[j][i]=num[j][i+1];
}
}
memset(dp,0,sizeof(dp));
for(int l=1;l<=tot;l++)
{
for(i=1;i<=tot;i++)
{
j=i+l-1;
if(j>tot) break ;
for(k=0;k<=num[c[j]][j+1];k++)
{
dp[i][j][k]=dp[i][j-1][0]+(len[j]+k)*(len[j]+k);
for(p=last[j];p>=i;p=last[p])
{
dp[i][j][k]=max(dp[i][j][k],dp[i][p][len[j]+k]+dp[p+1][j-1][0]);
}
}
}
}
ans=dp[1][tot][0];
}
int main()
{
int i,j,test,ca=0;
scanf("%d",&test);
while(test--)
{
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
tot=0;
memset(len,0,sizeof(len));
for(i=1;i<=n;)
{
tot++;
c[tot]=a[i];
while(i<=n&&a[i]==c[tot]) i++,len[tot]++;
}
solve();
printf("Case %d: %d\n",++ca,ans);
}
return 0;
}