【九度】题目1539：师弟

题目地址：http://ac.jobdu.com/problem.php?pid=1539
题目描述：

开学了，GrassLand的新师弟也来了，于是GrassLand打算去路口接他，以表兄长之谊。
已知：
共有n个路口，n个路口间存在着m条道路，每条道路连接两个路口，道路有其各自的长度。
GrassLand和他的实验室在1号路口，而他的师弟在n号路口。
师弟沿着最短路径走向实验室，若有多于一条的最短路径，他会任意选择一条。
GrassLand不希望走的太远而浪费科研的时间，所以他至多只会离开实验室k个路口。
问题出现了，GrassLand并不知道他的师弟会选择哪条路径。所以他想知道，所有离开实验室不超过k个路口（即该路口和实验室可以由至多k条道路连接）的路口中，在师弟和实验室间任意一条最短路径上的路口个数(包括实验室所在的1号路口和师弟所在的n号路口)。

输入：

输入包含多组测试用例。
每组测试用例开头为三个整数n（2 <= n <= 1000），m（1 <= m <= 100000），k(0 <= k <= 1000)
接下去m行描述道路信息，每行三个整数a(1 <= a <= n),b(1 <= b <= n && b != a),c(1 <= c <= 1000)，表示连接路口a和路口b的道路长度为c。
数据保证1号路口和n号路口间连通。

输出：

对于每组测试用例，输出一个整数，代表符合条件的路口个数。

样例输入：

4 3 2
1 2 1
2 3 1
3 4 1
4 3 1
1 2 1
2 3 1
3 4 1
4 4 1
1 2 3
1 3 2
2 4 2
3 4 3

样例输出：

3
2
3

题目比较晦涩难懂。看了好长时间。
其实最后所要求的是这样的结果。
从实验室到师弟所在的n，可能存在多条最短路径。
师兄从实验室出发，走的路口都在最短路径上。
假设他走了k个路口，问这满足这样条件的路口有几个。
举例说明：
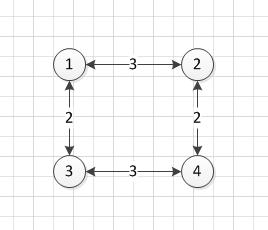
第一个例子，画成图是这样的：

最短路径只有一条。如果离开实验室2个路口，那么这样的路口是1,2,3.
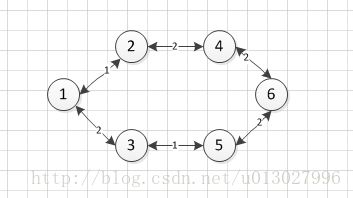
第三个例子，画成图是这样的：

存在的最短路径有两条。分别是1、2、4和1、3、4；
那么师兄离开实验室1个路口，他需要在最短路径上，那么他可以走1、2或者1、3。路口就是三个。
再举个例子。

存在的最短路径有两条。分别是1、2、4、6和1、3、5、6；
那么师兄离开实验室2个路口，他需要在最短路径上，那么他可以走1、2、4或者1、3、5。路口就是5个。
基本思想还是dijkstra+bfs；
dijkstra求最短路的时候，从实验室开始一次，从师弟开始一次。
再bfs的时候，就可以根据minLen1[s] + minLen2[s] == len来判断该点是不是最短路径上的点。
给两个测试用例
//测试数据
4 4 1
1 2 3
1 3 2
2 4 2
3 4 3
6 6 2
1 2 1
1 3 2
2 4 2
3 5 1
4 6 2
5 6 2
//结果
4
5

C++ AC

#include <stdio.h>
#include <string.h>
#include <queue>
using namespace std;
#define INF 10000000;
const int maxn = 1002; 
int path[maxn][maxn];
int minLen[2][maxn];
int visited[maxn];
int n,m,k;
void dijkstra(int s, int rank){
    int i,j;
    minLen[rank][s] = 0;
    visited[s] = 1;
    int minj = s;
    for(i = 1; i < n+1; i++){
        int min = INF;
        for(j = 1; j < n+1; j++){
            if(visited[j] == 0 && minLen[rank][j] < min){
                min = minLen[rank][j];
                minj = j;
            }
        }
        visited[minj] = 1;
        for(j = 1; j < n+1 ; j++){
			int sum = (minLen[rank][minj] + path[minj][j]);
            if (visited[j] == 0 && minLen[rank][j] > sum) {
                minLen[rank][j] = sum;
            }
        }
    }
}
int bfs(int len){
    queue<int> q; 
    while(!q.empty()) q.pop();  
    q.push(1);  
    int num = 0;
    int allNum = 0;
    visited[1] = 1;
	//这里是bfs，针对每一个搜索到的点，判断是否为关键路上的点
    while (!q.empty()) { 
        int size = q.size();
        if(num > k){
            return allNum;
        }
        num++;
        while(size --){
            int s = q.front();
            q.pop();
            if(minLen[0][s] + minLen[1][s] == len){
                allNum++;
            }
            for(int i = 1; i < n+1; i++){
            //  printf("%d\n",path[s][i]);
                if(visited[i] == 0 && path[s][i] < 10000000){
                    visited[i] = 1;
                    q.push(i);
                }
            }
        }
    }
    return allNum;
}
int main(){
    int i,j;
    while(scanf("%d%d%d",&n,&m,&k) != EOF){
        for(i = 1; i < n+1; i++){
            for(j = 1; j < n+1; j++){
                path[i][j] = INF;
            }
        }
        for(i = 0; i < m; i++){
            int a,b,d;
            scanf("%d%d%d",&a,&b,&d);
            if(path[a][b] > d){
                path[a][b] = d;
                path[b][a] = d;
            }
        }
        memset(visited,0,sizeof(visited));
        for(i = 1; i < n+1; i++){
            minLen[0][i] = path[1][i];
            minLen[1][i] = path[n][i];
        }
        dijkstra(1,0);
        memset(visited,0,sizeof(visited));
        dijkstra(n,1);
        memset(visited,0,sizeof(visited));
        int allNum = bfs(minLen[0][n]);
        printf("%d\n",allNum);
    }
    return 0;
} 
 
/**************************************************************
    Problem: 1539
    User: wangzhenqing
    Language: C++
    Result: Accepted
    Time:650 ms
    Memory:4988 kb
****************************************************************/

Java AC

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
 
public class Main {
    /*
     * 1539
     */
    private static int n,k;
    private static int path[][],visit[];
    public static void main(String[] args) throws Exception {
        StreamTokenizer st = new StreamTokenizer
				(new BufferedReader(new InputStreamReader(System.in)));
        while (st.nextToken() != StreamTokenizer.TT_EOF) {
            n = (int) st.nval;
            st.nextToken();
            int m = (int) st.nval;
            st.nextToken();
            k = (int) st.nval;
//          初始化路径，都为最大值。
            path = new int[n+1][n+1];
            for (int i = 1; i < n+1; i++) {
                for (int j = 1; j < n+1; j++) {
                    path[i][j] = Integer.MAX_VALUE;
                }
            }
            for (int i = 0; i < m; i++) {
                st.nextToken(); 
                int a = (int) st.nval; 
                st.nextToken(); 
                int b = (int) st.nval; 
                st.nextToken(); 
                int d = (int) st.nval; 
                if (path[a][b] > d ) {
                    path[a][b] = d;
                    path[b][a] = d;
                }
            }
             
            int minLen1[] = new int[n+1];
            int minLen2[] = new int[n+1];
//          visit初始为0，防止回溯
            visit = new int[n+1];
//          初始化1到其他点的距离。
            for (int i = 1; i < n+1; i++) {
                minLen1[i] = path[1][i];
                minLen2[i] = path[n][i];
            }
            dijkstra(path , minLen1 ,visit ,1);
            Arrays.fill(visit, 0);
            dijkstra(path , minLen2 ,visit ,n);
            Arrays.fill(visit, 0);
            int allNum = bfs(minLen1,minLen2,minLen1[n]);
            System.out.println(allNum);
        }
    }
     
    private static int bfs(int[] minLen1, int[] minLen2, int len) {
        int allNum = 0;
        Queue<Integer> queue = new LinkedList<Integer>();
        queue.add(1);
        visit[1] = 1;
        int num = 0;
        while (!queue.isEmpty()) {
            if (num > k) {
                return allNum; 
            }
            num++;
            int size = queue.size();
            while (size > 0) {
                int s = queue.poll();
                if (minLen1[s] + minLen2[s] == len) {
                    allNum++;
                }
                for (int i = 1; i < n+1; i++) {
                    if (visit[i] == 0 && path[s][i] != Integer.MAX_VALUE) {
                        queue.add(i);
                        visit[i] = 1;
                    }
                }
                size--;
            }
        }
        return allNum;   
    }
 
    private static void dijkstra(int[][] path, int[] minLen,
            int[] visit , int s) {
        minLen[s] = 0;
        visit[s] = 1;
        for (int i = 1; i < n+1; i++) {
            int min = Integer.MAX_VALUE;
            int minj = s;
            for (int j = 1; j < n+1; j++) {
                if (visit[j] == 0 && minLen[j] < min) {
                    min = minLen[j];
                    minj = j;
                }
            }
            visit[minj] = 1;
            for (int j = 1; j < n+1; j++) {
                if (visit[j] == 0 && minLen[j] > (minLen[minj] + path[minj][j])
                        && minLen[minj] != Integer.MAX_VALUE && path[minj][j] != Integer.MAX_VALUE) {
                    minLen[j] = minLen[minj] + path[minj][j];
                }
            }
        }
    }
}
/**************************************************************
    Problem: 1539
    User: wangzhenqing
    Language: Java
    Result: Accepted
    Time:1980 ms
    Memory:44684 kb
****************************************************************/