The Stable Marriage Problem 稳定婚姻问题与应用

本文由两篇网文组合而成，严格来说是转载

From: http://hi.baidu.com/acmdearway/blog/item/cd6804fdf1098888b901a01d.html/cmtid/132effa989853bbecb130cde

问题描述

稳定婚姻是组合数学里面的一个问题。

问题大概是这样：有一个社团里有n个女生和n个男生，每位女生按照她的偏爱程度将男生排序，同时每位男生也按照自己的偏爱程度将女生排序。然后将这n个女生和n个男生配成完备婚姻。

如果存在两位女生A和B，两位男生a和b，使得A和a结婚，B和b结婚，但是A更偏爱b而不是a，b更偏爱A而不是B，则这个婚姻就是不稳定的，A和b可能背着别人相伴而走，因为他俩都认为，与当前配偶比起来他们更偏爱各自的新伴侣。

如果完备婚姻不是不稳定的，则称其是稳定的。通过证明，可以得到每一个n女n男的社团，都存在稳定婚姻的结论。但是这种情况只在异性的社团中存在。也就是说在同性的社团里面，稳定婚姻的存在性将不再被保证。

Gale-Shapley 算法描述

 while 存在男人m是自由的且还没对每个女人都求过婚
    选择这个男人m
    令w是m的优先表中还没求过婚的最高排名的女人
    if w是自由的 
      （m，w）变成约会状态
    else w当前与m1约会
      if w更偏爱m1而不爱m
        m保持自由
      else w更偏爱m而不爱m1
        （m，w）变成约会状态
        m1变成自由
      endif
    endif
 endwhile

Gale-Shapley 算法在人人网“恋上某某某”应用中的应用

内容源自 http://blog.renren.com/blog/233941145/722556135#nogo

一、首先，我们来说明一下，为什么会发生两个人都相互喜欢，却没有表白这种情况呢。用通俗的话来说，就是大家都害怕表白后，被对方拒绝。

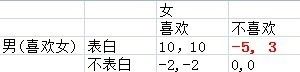
用形式化的博弈论来说明就是，假设A男喜欢B女，这时候他不知道该不该表白，他画了一个收益矩阵如下：（数字取的比较随意，明白意思就行了，别较真）

简单解释一下：1、双方都相互喜欢，而且一方表白了，那很好，收益都为10。2、假如A表白了，对方不喜欢他，那么就悲剧了，他收益为-5。3、假如他没表白，而B也喜欢他，那么他们就彼此错过对方而悲剧了。4、假如没表白，而且b也不喜欢他，那么双方都没什么损失，也没什么收益。

这个博弈没有纯策略的纳什均衡的解，而人们之所以有时选择了暗恋而非表白，是因为畏惧于那-5的损失。

而“恋上某某某”这应用，为了鼓励人们表白，采用的机制是

“1.假如你选择的暗恋对象也选择了你，双方都会得到通知。2、假如对方没有选择你，什么也不会发生，她也不知道你表白过。”

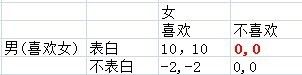
所以说，这个应用其实是把博弈的矩阵转化为：

在这种情况下，“表白”这一策略相对于“不表白”占优。人们不用担心表白失败后的损失，因此可以大胆的去表白了。

以上是把一些大家都明白的简单道理，用博弈论这稍微严谨一点的方法表示一下。

 

二、如何扩展这个应用（纯属YY）

今天看到一人说“理性人肯定会全选暗恋的，这样就能知道谁暗恋我，然后自个儿慢慢挑。于是这个机制就失效了。” 

这是很有道理的，试想一下，假如大家都这么玩的时候，可能会出现什么问题呢？情景1：A选择了暗恋几个好友，同时他发现他暗恋的B也选择了暗恋他，这是他一阵窃喜，马上去联系B；结果B告诉A说：“不好意思，我同时选择了暗恋C和A，C也暗恋了我，而我喜欢C胜过A，所以最终选择了C而放弃了A”。于是，A就悲剧了。

这是一个存在了多年的问题，类似的情况出现在“高校录取”、“找工作”等情况下，问题的根源是，一个申请者会申请多个学校，他总是希望去读一个他收到offer的最好的学校；因此，学校给学生发了offer，学生也不一定会来，找工作的时候也经常有违约现象发生。为了解决这些问题，常见的有高考中的分批录取，还有waiting list等手段。

如何完美的解决这个问题呢？计算机科学里有个叫“gale sharply”的算法，完美的解决了这个问题。这个算法的核心思想是，对于n男n女，假如我们知道每一个人对于异性的偏好关系，我们可以给出一个稳定的matching，使得没有“unstable matching”的存在，而unstable matching指的是 “如果John和Ivy，Gary和Kate配对，而John更喜欢Kate，Kate更喜欢John。那么John和Kate就会私奔,那么这个配对就是 unstable的了。”。具体的介绍可以看http://www.elly66.com/maths/stable-matching-problem。

具体在我们的问题上，可以这么应用，假设许多单身的人都用了“恋上某某某”这个应用，那么对于每个用户，我们不仅让他提交出他暗恋那些用户，而且让他根据喜欢程度对这些人排个序，最终运行一个gale sharply算法，找出stable matching，再给双方互相发信。

例如，在上面A、B、C的例子里，假如把A和B配对了，就是一个unstable matching，因为B更喜欢C，而且C也喜欢B，他们可能会私奔的。所以，应用Gale Sharply算法，就是为了避免让A和B这样不稳定的配对产生，从而避免了A被放鸽子的厄运。所以，在新的场景里，如果A最终没有收到B的信，只能说明B找到了一个更喜欢的人C，这样避免了A被放鸽子的损失，而且假如A还有一个一般点喜欢的D，D也就多了一次和A相恋的机会。

Gale sharply算法有许多优点，最主要是防欺骗性也比较强，也就是说，在这个算法下，你的最优策略，就是按你自己真实的喜欢程度来提交用户；假如你提交了一个虚假的偏好顺序，可能会让你失去和一个你更喜欢的人配对的机会。

在这想起了2年前看的陈楸帆写的一篇《虚拟的爱》的科幻，文中就描述了一个人们的恋爱关系，都靠机器通过这种算法来安排的时代。假如大家给“恋上某某某”都提交了许多的数据，是不是我们离这个时代就近了一步呢？当然了，这纯属YY，在绝大部分情况下，不加gale sharply算法的 "恋上XXX"，即使出现了冲突，让人们自行去解决就好了～

总结：所以说，有时候科幻和现实的距离的确挺近的。而且有些时候，现实比科幻还好玩：科幻只能想想，在现实中你还有实现它的机会～